Bootstrap
Nesse post apresentaremos a técnica estatística Bootstrap. Nada melhor do que um exemplo de brigadeiro para termos um gostinho inicial sobre o tema.

Imagine que você seja dono de uma loja de doces. Um cliente espera que, ao comprar um brigadeiro, este tenha, em média, o mesmo peso que o de outro cliente. No entanto, é impossível pesar todos os brigadeiros que serão produzidos pela sua loja!!
O que fazer então??
Você, dono do estabelecimento, pode utilizar técnicas de amostragem capazes de selecionar aleatoriamente 150 brigadeiros e calcular o peso médio desses brigadeiros. Feito isso, poderá concluir que a média da população está dentro de uma margem de erro relativa à média da amostra.
Suponha que você queira saber, após alguns meses, qual o peso médio do brigadeiro no dia em que foi feita uma amostra da linha de produção levando em conta uma maior precisão.
Como diversas variáveis surgiram, não podemos mais usar como base o brigadeiro produzido hoje. Dentre essas variáveis consideramos os diferentes tipos de açúcar, cacau e manteiga, novos sabores, o tipo de confeito, o recheio, entre outros.
Assuma que a única informação que temos é o peso daqueles 150 brigadeiros na data de teste inicial. E, podemos considerar a margem de erro inicial como nossa informação mais relevante.
Felizmente, para solucionar esse problema existe o
Bootstrap!! 
Dessa forma, criamos nossa amostra Bootstrap, que surge a partir da amostragem aleatória dos 150 pesos conhecidos. Caso seja permitida a reposição dos pesos, essa amostra bootstrap não será necessariamente idêntica à inicial. Alguns dados podem estar omitidos e outros repetidos. Assim, inúmeras amostras bootstrap são rapidamente criadas com ajuda computacional.
Visão técnica
Vamos agora apresentar o Bootstrap com mais detalhes.
Essa técnica estatística foi inicialmente proposta por Bradley Efron, em 1979. Ela vem ganhando força, em especial, devido ao avanço computacional.
O termo Bootstrap tem origem inglesa e faz referência ao laço da parte de trás de uma bota que o auxilia a calçá-la.
Seu uso surge da frase “To lift himself up by his bootstraps.”, ou seja, “Erguer-se utilizando seu bootstrap”. Ocorre aqui uma alusão a algo impossível, de difícil realização.
Imagine levantar-se no ar puxando apenas pedaços de couro de sua bota. Isso é impossível! E a ideia que esse modelo quis trazer é a de poder fazer o impossível.
A história do Barão Munchausen, também mencionada na origem do Bootstrap, conta que o Barão conseguiu erguer a si e o seu cavalo de um pântano por meio de seu cabelo (especificamente, seu rabo de cavalo). No entanto, na história não há o uso da palavra bootstrap como a conhecemos e nenhuma outra referência explícita aos bootstraps foi encontrada em outras partes das várias versões dos contos Munchausen.


Teoria
Pense no caso de uma amostra aleatória de tamanho n , a partir de uma função de distribuição de probabilidade F indefinida: \(X_i=x_i, X_i\) \(\sim\) \(F_{ind}\), \(i=1,2,...,n\).
Sejam \(X= (X_1,X_2,...X_n)\) e \(x=(x_1,x_2,...,x_n)\) as variáveis aleatórias e as observações das variáveis aleatórias independentes, com função de distribuição comum F. Vamos investigar a variabilidade e a distribuição amostral do cálculo da estimativa local a partir da amostra de tamanho n. Denotamos essa estimativa local como \(\widehatθ\). Note que \(\widehatθ\) é uma função das variáveis aleatórias \((X_1,X_2,...X_n)\) e, por isso, possui uma distribuição de probabilidade, sua distribuição amostral, que é determinada por n e F.
Com base em Efron and Tibshirani (1993), os passos básicos para criação do Bootstrap são:
Passo 1:
Construa, a partir da amostra, uma distribuição de probabilidade empírica \(F_n\), inserindo, em cada ponto \(x_1,x_2,...x_n\) da amostra, uma probabilidade \(1/n\).
Caracterizada como uma função de distribuição empírica da amostra, esta é uma estimativa não paramétrica de máxima probabilidade da distribuição populacional, F.
Passo 2:
Realize a reamostragem: desenhe uma amostra aleatória de tamanho n com reposição a partir da função de distribuição \(F_n\).
Passo 3:
Calcule para essa reamostragem a estatística de interesse \(T_n\), gerando \(T_n^*\).
Passo 4:
Repita os passos 2 e 3 B vezes. Para criar B reamostras, B deve ser um valor grande. O tamanho de B depende de testes a serem realizados com os dados. Quando uma estimativa com intervalo de confiança de \(T_n\) é necessária, sugere-se que B seja ao menos igual à 1000.
Passo 5:
Construa a partir do valor B de \(T_n\) a frequência relativa do histograma, atribuindo probabilidade de \(1/B\) à cada ponto \(T_n^1\), \(T_n^2\),…, \(T_n^B\).
A distribuição obtida é a estimativa Bootstrap da distribuição amostral de \(T_n\). Pode-se realizar inferências sobre o parâmetro θ, utilizando essa distribuição, estimando \(T_n\).
Bootstrap e ações do mercado financeiro utilizando o R
No exemplo a seguir, criaremos a amostra Bootstrap para os retornos diários das ações da Apple e do índice S&P500 de 02/06/2016 a 31/05/2017. Para tanto, primeiro baixe a base bootstrap.txt que está disponível no link. Faça a leitura dessa base no R conforme demonstrado no código abaixo:
dados<-read.table(file.choose())
Para trabalhar com a base digite o seguinte comando:
spxret <- dados[, 'SP500index']
applret <- dados[,'APPLE']
names(dados)[names(dados)=="SP500index"] <- "sp500"
dados$sp500 <- as.numeric(as.character(dados$sp500))
dados$sp500<-c(NA,diff(log(dados$sp500)))
dados$APPLE<-c(NA,diff(log(dados$APPLE)))
spxret<-as.numeric(spxret)
Os comandos spxret e applret extraem uma coluna para criar um vetor. Nas linhas seguintes trabalhamos a base para transformar todos os dados em numéricos, retiramos NA’s e transformamos os retornos em log retornos.
Na nossa análise obtivemos, em um ano, 251 retornos diários. Aleatoriamente uma amostra bootstrap foi obtida dos retornos diários. No nosso caso, você observará que alguns dias estarão diversas vezes na amostra bootstrap enquanto outros nem aparecerão. Isso ocorre devido ao fato de realizarmos amostragem com reposição. A partir da nossa amostra bootstrap, optamos por realizar a soma dos valores. Tipicamente várias amostras bootstrap são criadas.
O código abaixo mostra como utilizar o Bootstrap para gerar 1000 amostras Bootstrap. Podemos observar abaixo que amostramos com inteiros de 1 a 251. Criamos uma amostra de tamanho 251 e a amostramos com reposição. Com o comando this.samp temos um ano com retornos diários que poderiam ter acontecido. Coletamos os retornos anuais para cada ano hipotético na linha de código seguinte.
spx.boot.sum <- numeric(1000) # numeric vector 1000 long
for(i in 1:1000) {
this.samp <- spxret[ sample(251, 251, replace=TRUE) ]
spx.boot.sum[i] <- sum(this.samp)
}
Você pode também plotar a distribuição dos retornos anuais obtidos com o Bootstrap com o código a seguir:
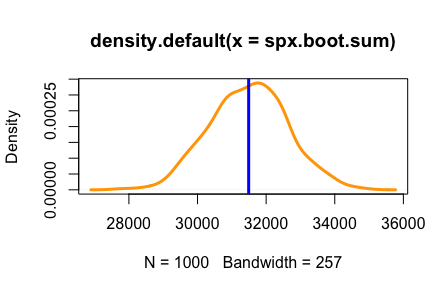
plot(density(spx.boot.sum), lwd=3, col="orange")
abline(v=sum(spxret), lwd=3, col='blue')
Segundo a imagem abaixo, o retorno anual é bastante variável. Caso você utilize uma base de dados inicial diferente, o seu gráfico sofrerá alterações. Nessa situação encontramos bem próximo ao meio da distribuição o nosso retorno anual. Vale ressaltar que esse resultado pode ser diferente devido a vieses estatísticos ou na base de dados.
Vamos praticar?
Referências
Efron, B. (1979). Bootstrap methods: another look at the jackknife. The annals of Statistics, 1-26.
Efron, B, and Tibshirani, R.J. (1993). An introduction to the bootstrap. Chapman and Hall, London.