Eventos, Probabilidade e Condicionalidade

No livro The History of Probability o autor Todhunter relata de forma cronológica considerações de aspectos elementares da Teoria da Probabilidade de alguns notáveis personagens da história. No entanto, os primórdios da probabilidade está relatado nas correspondências entre Pierre De Fermat e Blaise Pascal sobre um problema de jogos em lançamento de dados no século XVII, citados em Games, Gods & Gambling.

Probabilidade é a área da matemática responsável por mensurar aquilo que não é determinístico. Os resultados dos lançamentos de dados ou moedas são considerados experimentos de probabilidade, pois estão sujeitos ao acaso.

Para o cálculo de probabilidades, considere as seguintes abordagens:

• Clássica: “Suponha que dentre \(n\) resultados possíveis e equiprováveis \(m\) sejam favoráveis. A probabilidade de um evento favorável é \(p = \frac{m}{n}\).” Essa abordagem é o resultado das correspondências entre Fermat e Pascal.

• Frequentista: “Foram realizados \(n\) experimentos dos quais \(m\) eram favoráveis. A frequência relativa da ocorrência de um evento favorável é \(\frac{m}{n}\).” Jakob Bernoulli, em seu livro Ars Conjectandi, provou a convergência entre a frequência relativa de ocorrência e a probabilidade \(p\) clássica a medida que aumenta-se o número de experimentos \(n\).

Dito isso, vamos definir como \(P(A)\) a probabilidade de ocorrer o evento \(A\) em um determinado conjunto de valores possíveis \(\Omega\). Antes de tudo vamos aquecer o cérebro compreendendo os importantes conceitos de independência e permutabilidade para o estudo de probabilidade.

Independência

Seja uma caixa contendo 2 bolas brancas e 3 pretas. Considere o experimento da retirada aleatória e observância da cor da bolas, com representação Bernoulli (\(X_1\)) de ocorrência:

• \(X_1 = 0\) caso a bola retirada seja branca

• \(X_1 = 1\) caso a bola retirada seja preta

Pela abordagem clássica, a probabilidade da bola ser branca é \(P(X_1 = 0) = \frac{2}{5}\) e de ser preta \(P(X_1 = 1) = \frac{3}{5}\).

Após a primeira retirada, e sem reposição, você retira mais uma bola. Qual a probabilidade da segunda bola ser branca?

A resposta mais intuitiva é DEPENDE. De fato, a probabilidade da segunda retirada (\(X_2\)) está condicionada ao resultado da primeira. Perceba, caso a primeira seja branca, restam mais \(1\) branca e as demais \(3\) pretas, e, nesse caso, a probabilidade de uma segunda retirada branca é \(\frac{1}{4}\). Caso a primeira tenha sido preta, seria \(\frac{2}{4}\).

De maneira geral, a probabilidade do evento \(B\) condicionada ao evento \(A\) é representada por \(P(B/A)\). Nesse caso, temos que:

• \[P(X_2 = 0|X_1 = 0) = \frac{1}{4}\]
• \[P(X_2 = 0|X_1 = 1) = \frac{2}{4}\]

Dessa forma, dizemos que o evento \(X_2\) é dependente do evento \(X_1\).

A probabilidade conjunta dos eventos \(A\) e \(B\) é expressa pela regra do produto: \(P( B \cap A) = P(B|A) P(A)\) que também pode ser expressa por \(P( B \cap A) = P( B , A)\).

Considere agora um outro experimento, o lançamento de uma moeda honesta e a observância da face virada para cima. Considere a representação Bernoulli (\(X_1\)) de ocorrência:

• \(0\) caso o resultado do lançamento seja coroa

• \(1\) caso o resultado do lançamento seja cara

Por ser justa, a probabilidade do resultado cara é \(P(X_1 = 1) = \frac{1}{2}\) e o de coroa é \(P(X_1 = 0) = \frac{1}{2}\).

Em seguida, a moeda é lançada novamente e o resultado representado por \(X_2\). Perceba que nesse caso, a probabilidade da ocorrência de cara no segundo lançamento também é igual a \(P(X_2 = 1) = \frac{1}{2}\) por não ser afetado pelo resultado do primeiro lançamento.

Dizemos que \(X_2\) é independente de \(X_1\), e nesse caso, temos que a regra do produto é:

Permutabilidade

Permutabilidade é a propriedade da alteração no ordenamento de realizações em uma sequência de eventos sem que a probabilidade conjunta seja alterada.

Considere o lançamento de \(5\) moedas não viciadas, com representação semelhante a apresentada anteriormente, sendo observado o seguinte resultado \((1,0,1,1,0)\), isto é, (cara,coroa,cara,cara,cora). Sabemos que os lançamentos são independentes e que a probabilidade conjunta desse evento é \(P(1,0,1,1,0) = P(X_5 = 1) \times P(X_4 = 0)\times P(X_3 = 1)\times P(X_2 = 1)\times P(X_1 = 0) = \frac{1}{2^5}\).

Nessa situação, caso fosse observado o evento \((1,1,1,0,0)\), a probabilidade não seria alterada, pois \(P(1,0,1,1,0) = P(1,1,1,0,0) =\frac{1}{2^5}\). Dessa forma, a ordem da ocorrências dos resultados cara não altera a probabilidade conjunta, desde que seja a mesma quantidade de resultados de “sucesso”. Esse é uma versão não rigorosa do Teorema de De Finetti.

De maneira geral, a independência de uma sequência de eventos garante a permutabilidade da mesma.

No entanto, a permutabililidade não é condição necessária para a permutabilidade, apenas suficiente. Isto é, ainda que uma sequência não seja formada por eventos independente, é possível que sejam permutáveis.

Considere a mesma representação do exemplo da caixa com bolas apresentado anteriormente para o caso da retirada de \(5\) bolas sem reposição. Como visto, esses eventos não são independentes, pois a probabilidade de um determinado evento na sequência, depende do resultado observado nos eventos anteriores.

Dessa forma, vamos verificar se o evento \((1,0,1,1,0)\) é permutável. Inicialmente, vamos calcular a probabilidade \(P(1,0,1,1,0)\):

\(P(1,0,1,1,0) = P(X_1 = 1)\times P(X_2 = 0 | X_1 = 1) \times P(X_3 = 1 |X_2 = 0 , X_1 = 1) \times P(X_4 = 1|X_3 = 1 ,X_2 = 0 , X_1 = 1) \times P(X_5 = 0|X_4 = 1 , X_3 = 1 ,X_2 = 0 , X_1 = 1)\) \(P(1,0,1,1,0) = \frac{3}{5} \times \frac{2}{4} \times \frac{2}{3} \times \frac{1}{2} \times \frac{1}{1} = \frac{1}{10}\)

Agora, vamos calcular a probabilidade \(P(1,1,1,0,0)\), alterando o resultado do segundo e o quarto evento:

Dessa forma, embora essa sequência seja formada por eventos dependentes, a ordem desses eventos não altera a probabilidade conjunta, tornando-a permutável.

Teorema de Bayes

O teorema de bayes estabelece a seguinte relação entre dois eventos A e B, com probabilidades, respectivamente, P(A) e P(B):

Considerando os eventos \(A\) e \(B\) permutáveis, o termo \(P(A \cap B)\) é igual a \(P( B \cap A )\) e, dessa forma, pode ser escrita como:

Por fim, tem-se a seguinte relação:

Nesse caso, o probabilidade \(P(A)\) é denominada probabilidade a priori, isto é, a informação sobre o evento \(A\) antes que se soubesse algo sobre o evento \(B\). Mais adiante, quando se tenha conhecimento sobre \(B\), a probabilidade relacionada ao evento \(A\) deve ser atualizada pela probabilidade do evento \(B\). A probabilidade \(P(A/B)\) é agora denominada probabilidade a posteriori. Sendo a razão \(\frac{P(B/A)}{P(B)}\) o fator de atualização das informações sobre o evento \(A\).

Para compreender com mais detalhes o Teorema de Bayes é necessário entender a regra da probabilidade total (RPT), que expressa a probabilidade total de um resultado por meio de vários eventos disjuntos.

Inicialmente, considere o problema em encontrar o valor para a probabilidade do evento \(A\).

Considere agora que seja possível particionar o espaço \(\Omega\) em partes \(B_i\) sem intersecções entre si. Note que a união das partes \(B_i\) formam \(\Omega\).

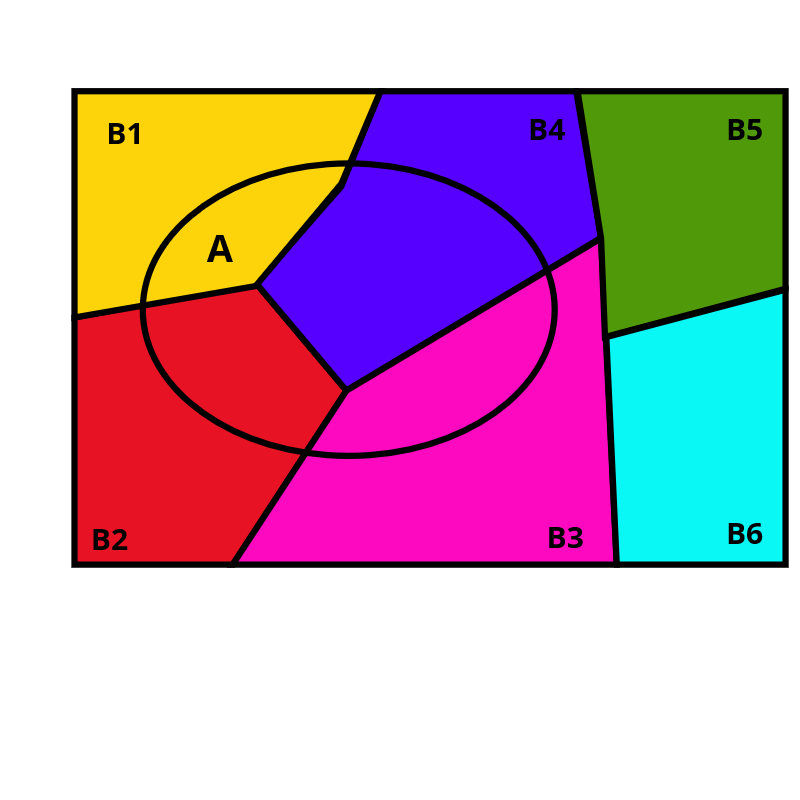
A probabilidade \(A\) pode ser determinada pela intersecção entre o evento \(A\) e cada partição \(B_i\).

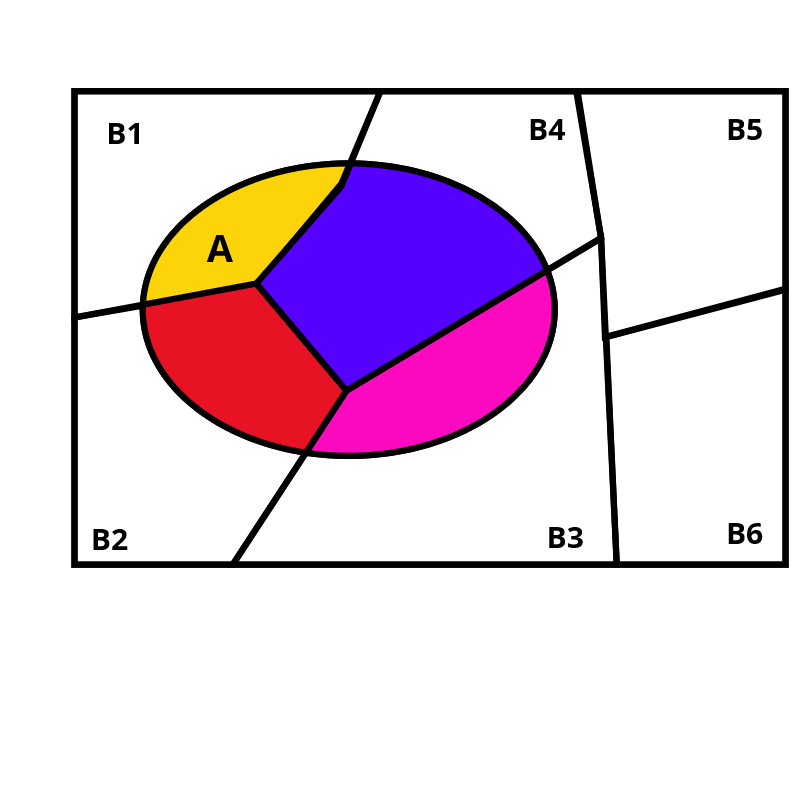
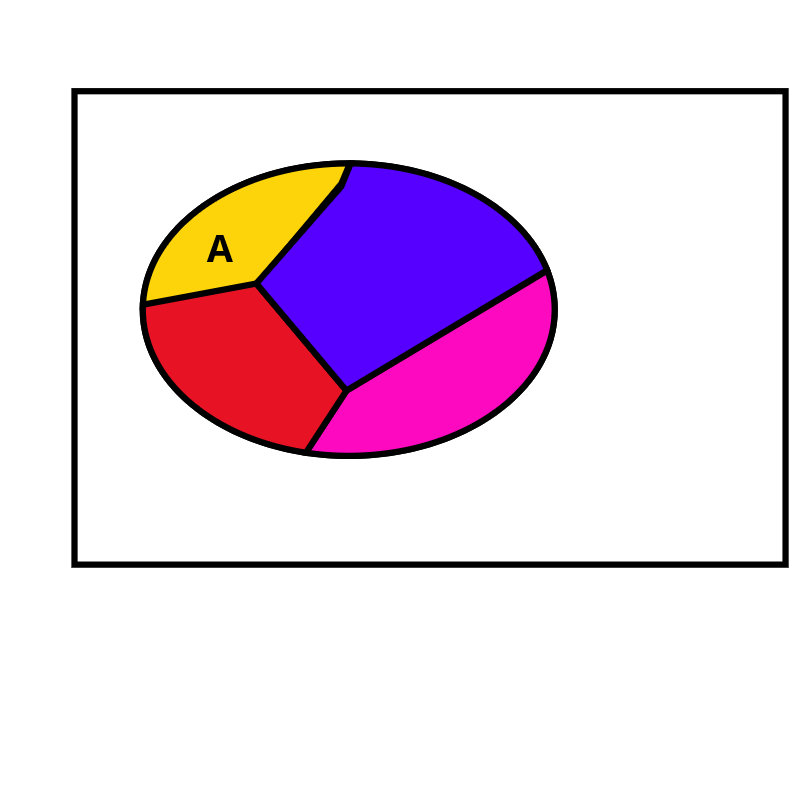
Nos espaços amostrais \(\Omega\) formados pela união de partes \(B_i\) disjuntas (mutuamente exclusivas) a probabilidade de qualquer evento de \(\Omega\) é:

\(P(A) = P(A \cap B_1) + P(A \cap B_2) + ... + P(A \cap B_N)\) \(P(A) = P(A | B_1)P(B_1)+P(A | B_2)P(B_2) + ... + P(A | B_N)P(B_N)\)

Dessa forma, a probabilidade do evento \(A\) pode ser representado por:

Qual a importância desse resultado?

Aplicação simples

Um amigo muito próximo lhe pediu \(R\$ 1.000,00\) emprestado (\(V_{emprestado}\)) para solução financeira de uma emergência. Você é um investidor nato e não suporta a ideia de perder o patrimônio conquistado. Embora você decida ajudar seu amigo, você está preocupado com o risco do não pagamento do empréstimo e, por isso, cobrará juros \(T_{juros}\) sobre o montante inicial emprestado:

Você percebeu que o valor devolvido (\(V_{devolvido}\)) do seu “investimento” ao final do período de empréstimo está sujeito às “variações do mercado”, que, nesse caso, estão relacionadas a um evento \textbf{incerto} do não pagamento da dívida. Com isso, você define o valor esperado (\(V_{esperado}\)) como o valor recebido ao final do período considerando tal incerteza.

Seja \(A\) o evento indicativo do pagamento do seu amigo, então o valor esperado (\(V_{esperado}\)) ao final do período de empréstimo é a média ponderada entre as possibilidades de valores devolvidos, \(V_{devolvido}\) e \(0\), e suas respectivas probabilidades, \(P(A)\) e \(1 - P(A)\):

\(V_{esperado} = V_{devolvido} \times P(A) + 0 \times [1 - P(A)]\) \(V_{esperado} = [V_{emprestado} \times (1 + T_{juros})] \times P(A) + 0 \times [1 - P(A)]\) \(V_{esperado} = [V_{emprestado} \times (1 + T_{juros})] \times P(A)\)

Da relação anterior, é possível obter a a taxa de juros adotada:

Você decide que o valor dos juros será determinado de maneira que o valor esperado seja igual ao investimento inicial, isto é, \(V_{esperado}=V_{emprestado}\). Dessa forma, a taxa de juros utilizada será:

Você utilizará uma proxy o evento \(A\) baseado no cadastro nacional de bons ou maus pagador. Infelizmente, você não tem acesso à esse cadastro. No entanto, você sabe que, assim como você, seu amigo possui conta no banco ABC, que regularmente publica informações agregadas sobre as operações com os clientes.

Tal banco realizou um levantamento informando que \(1\) em cada \(10\) clientes possuem registo ativo no cadastro nacional de maus pagadores. Dessa forma, a probabilidade do pagamento do seu amigo se concretizar é de \(P(A)=\frac{9}{10} = 90\%\).

Dito isso, utilizando a taxa de juros que você deve adotar é: \(T_{juros} = \frac{1}{0.9} - 1 = 11.111\%\)

Dessa forma, a priori, seu amigo deveria lhe pagar R$ \(1.111,11\) ao final do período para garantir que, em média e desconsiderando inflação, seu investimento inicial seja recuperado.

Nos informativos do banco também consta que \(2\) em cada \(4\) maus pagadores atrasam o pagamento do boleto, enquanto dentre os bons pagadores, apenas \(1\) a cada \(20\) atrasam suas obrigações.

Durante a conversa, seu amigo te informou que possui boletos atrasados nesse banco. Baseado nessa nova informação, qual a probabilidade do seu amigo ser mau pagador dado que atrasou o pagamento? Qual a nova taxa de juros que você deve adotar para proteger seu “investimento”?

O Teorema de Bayes responde diretamente essa pergunta. Antes disso, vamos modelar os eventos e identificar suas probabilidades. Considere o evento \(A\) o cliente ser um bom pagador e o evento \(B\) o atraso do pagamento de um boleto da obrigação financeira nesse banco.

• Ser bom pagador: evento \(A\). Sendo \(P(A)=\frac{9}{10}\).
• Ser mal pagador: evento \(A^{c}\). Sendo \(P(A^{c})=1-P(A)=\frac{1}{10}\).
• Atraso no pagamento: evento \(B\). Sendo \(P(B)=\) não informado.
• Atraso no pagamento dos bons pagadores: evento \(B/A\). Sendo \(P(B/A)=\frac{1}{20}\).
• Atraso no pagamento dos mal pagadores: evento \(B/A^{c}\). Sendo \(P(B/A^{c})=\frac{2}{4}\).
• Probabilidade do seu amigo ser bom pagadores caso tenha atrasado o pagamento. \(P(A/B)=\)?.

Utilizando o Teorema de Bayes e a RPT em \(P(B)\), tem-se que:

Dessa forma, após saber que ele não pagou o boleto do banco, a probabilidade de ser bom pagador a posteriori reduz em quase a metade da priori. Dessa forma, a nova taxa de juros é \(\frac{1}{0.4736} - 1 = 111.111\%\), fazendo com que o valor cobrado seja de R$ \(2.111,11\).

Esse é uma versão introdutória do Teorema de Bayes e serve para motivação para posts futuros que exigirão mais pré requisitos em teoria de probabilidades. Enquanto isso, vamos ver uma aplicação me modelos de séries temporais das propriedades do Teorema de Bayes.

Modelos de Espaços de Estados

Os modelos de Espaços de Estados são uma classe de modelos utilizados para estudar e conhecer séries temporais, conjunto de valores observados ao longo de instantes no tempo, podendo ser representado por \((Y_t)_{(t>0)}\), sendo \(t=1,2,\cdots,T\) o indexador que representa o instante de mensuração da quantidade.

Considere a seguinte estrutura de dependência para a série temporal \(Y_t\):

É importante notar que a \(Y_1,Y_2,....,Y_T\) é condicionamente independente por meio de uma função do parâmetro \(\theta\). Em outras palavras, as informações em \(t\) são independentes das em \(t-1\), condicionadas a informação de \(\theta\). Como exemplo, para \(t=2\), essa relação é determinada pelo resultado \(P(Y_2/Y_1,\theta) = P(Y_2/\theta)\). Para \(t\) qualquer, tem-se que \(P(Y_t/Y_1,Y_2,...,Y_{t-1},\theta) = P(Y_t/\theta)\).

Essa propriedade permite que a distribuição conjunta dessa série possa ser reescrita por:

Replicando esse procedimento para a série inteira, não é difícil chegar a seguinte resultado:

Dessa forma, a distribuição conjunta dessa série é incrementada sequêncialmente a cada nova informação \(Y_t\) por meio da distribuição condicional \(P(Y_t/\theta)\). Dessa relação, é possível obter atualizações sobre \(\theta\). Vamos entender esse conceito com o estudo de um caso.

Modelos Gaussianos

Um investidor está interessado em conhecer melhor o comportamento dos retornos mensais do Índice Ibovespa utilizando a estrutura de dependência apresentada anteriormente:

Com \(\epsilon_t \sim N(0,\sigma^2)\), sendo \(\sigma^2\) conhecido e igual a \(5\). Nesse caso, temos a dependência condicional \(Y_1,Y_2,...,Y_T/\theta \sim N(\theta,\sigma^2)\)

Conversando com colegas ele obteve a informação inicial de que o comportamento da média dos retornos mensais (\(\theta\)) tem distribuição Normal como média \(\eta_0=2\) e variância \(\phi_0^2 = 2\). Essa é a informação a priori do parâmetro da série temporal de interesse. Com base nessa informação, o investidor pretende observar os índices ao final de cada mês e atualizar o conhecimento sobre \(\theta\), a distribuição a posteriori, a medida que novas observações da série do índice mensal do Ibovespa \(Y_t\) estejam disponíveis.

Sabendo que o valor do índice Ibovespa para janeiro de 2017 foi \(Y_1=7.38\), qual é a distribuição e os parâmetros da posteriori \(P(\theta/Y_1)\)?

Ao final do primeiro mês o investidor pretende obter a distribuição \(P(\theta/Y_1)\) e para isso utiliza o Teorema de Bayes, chegando a seguinte relação:

O desafio, nesse ponto, é obter a distribuição conjunta \(P(Y_1,\theta)\) por meio do produto entre a probabilidade da série \(Y_1\), \(P(Y_1/\theta)\), e a priori do parâmetro \(\theta\), \(P(\theta)\). Utilizando informaçõe das distribuições normais informadas, temos que:

Perceba que, a menos de constantes, essa distribuição conjunta tem o núcleo de uma distribuição normal com média:

e variância

Perceba que o denominador é a integração dessa distribuição conjunta (numerador) com relação a \(\theta\) e, com um pouco de esforço algébrico, é a constante normalizadora. Mais detalhes dos processo podem ser consultados em Petris et al (2009).

Dessa forma, temos que \(\theta/Y_1 \sim N(3.53,1.42)\). Essa é a distribuição a posteriori de \(\theta\) com relação a informação \(Y_1\). O gráfico a seguir apresenta a comparação entre as distribuições priori e posteriori.

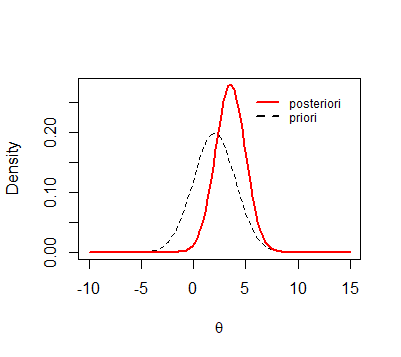
A distribuição a posteriori tem seus parâmetros \(\eta_t\) e \(\phi_t\) atualizados no instante \(t\) a medida que se tenha acesso a novas informações da série temporal. Em todos esses instantes, a posteriori obtida no passo \(t\) é a nova priori para a estimação em \(t+1\).

A repetição do processo de estimação em um instante \(t\) qualquer fornece o seguinte resultado:

Sendo \(\eta_t\) a média entre a o valor inical \(\eta_0\) e a média da série \(Y_1,...,Y_t\) ponderados pelas variâncias do processo:

e a variância

A programação em R a seguir calcula os valores a posteriori a cada nova observação do índice Ibovespa para o ano 2017. Note que em cada período são utilizadas as informações acumuladas até o instante de análise, determinado pelo comando “y[1:i]”.

## IBOV time series 2017
y <- c(7.38,3.08,-2.52,0.64,-4.12,0.3,4.8)

## parameters      
sigma <- 5
eta   <- 2
phi   <- 2

## posteriori eta
etat <- function(y,sigma,eta,phi){
  t <- length(y)
  return((mean(y)*phi + eta*sigma/t)/(phi + sigma/t))
}

## posteriori phit
phit <- function(y,sigma,phi){
  t <- length(y)
  return((phi *sigma)/(t*phi +sigma ))
}


## storing posteriori values 
mus <- NULL
ss <- NULL

for(i in 1:length(y)){
  mus <- c(mus,etat(y[1:i],sigma,eta,phi))
  ss  <- c(ss,phit(y[1:i],sigma,phi))
}

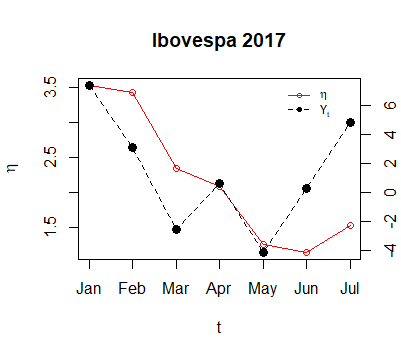
O gráfico a seguir apresenta os retornos mensais do Ibovespa durante 2017 e o valor médio a posteriori do parâmetro \(\theta\).

## first axis eta
plot(mus, type="o",main = "Ibovespa 2017",
     ylab=expression(eta),xlab = "t",xaxt='n',col  = "red")

axis(side = 1, at =1:7,
     labels = c("Jan","Feb","Mar","Apr","May","Jun","Jul"))

legend(x = 5.5,y= 3.6,
       legend=c(expression(eta), expression(Y[t])),
       lty=c(1,2), pch=c(1, 16), col=c("red", "black"),box.col=0,cex = .75)

## second axis ibov time series
par(new = T)
plot(y = y,x = (1:7)/8, type="o", pch=16, lty=2, axes=F, xlab=NA, ylab=NA, cex=1.2)
axis(side = 4)
mtext(side = 4, line = 3, expression(y_t))

Considerações finais

O conteúdo do post, embora simples, apresenta de que maneira a Teoria Bayesiana é utlizada para modelos de séries temporais, permitindo que haja a atualização do conhecimento a medida que se tenha acesso a novas informações.

Por fim, é possível destacar três avanços em estudo nessa área:

• estrutura de dependência temporal que incorpore tendência e sazonalidade

• relações não gaussianas e não-lineares.

• aumentar número de parâmetros desconhecidos ( ex.: \(\sigma^2\))

O aumento da complexidade requer a utilização de técnicas estatísticas e computacionais mais sofisticadas para lidar com o processo de estimação. É comum encontrar distribuições a posteriori que não tenham formas fechadas ou situações com alta dimensão em virtudo da quantidade de parâmetros e tamanho da série temporal. Nesses casos, técnicas como Bootstrap, MCMC, Gibbs Sampler e Filtro de Partículas podem ser adotadas.

Referências

Todhunter, Isaac (1873). History of the Mathematical Theories of Attraction and Figure of the Earth from Newton to Laplace.

David, F. N. (1962). Games, gods and gambling.

Petris, Giovanni, Sonia Petrone, and Patrizia Campagnoli. (2009). Dynamic Linear Models With R.

• ← Previous Post
• Next Post →