Conteúdo

Introdução
Intuição
Matemática
Código
Referências

Introdução

Uma das grandes vantagens de Aprendizado de Máquina é conseguir estimar funções com relações complexas entre as variáveis e cheias de não linearidade. Se quisermos encarar esses problemas com modelos lineares simples, podemos extender a forma funcional estimada usando mais parâmetros, o que pode ser obtido, por exemplo, fazendo uma expansão polinomial. Sempre podemos aumentar o grau do polinômio estimado, tornando-o arbitrariamente complexo, para assim conseguir ajusta-lo a dados bastante não lineares.

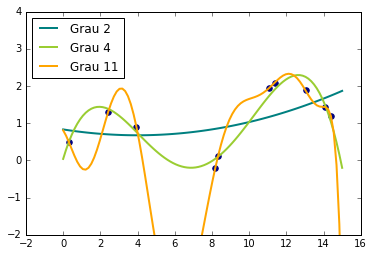
Por outro lado, e se não quisermos especificar de antemão o número de parâmetros do modelo? Uma possibilidade é considerar todas as funções que se encaixam nos nossos dados, cada uma com quantos parâmetros forem necessários. É isso que Processos Gaussianos são capazes de fazer: um método não paramétrico para regressão não linear. Note que não paramétrico não deve ser confundido como um modelo sem parâmetros, mas sim entendido como algo que tem muitos parâmetros (infinitos, possivelmente), tanto mais quanto maior for a quantidade de dados.

Mais do que isso, Processos Gaussianos são modelos probabilísticos ou bayesianos. Isso significa que, além de nos fornecer uma estimativa pontual de uma previsão (geralmente a média condicional), os Processos Gaussianos também especificam toda a distribuição preditiva a posteriori, tornando a obtenção de estatísticas de incerteza algo natural. Isso é extremamente importante para aplicações de Aprendizado de Máquina em cenários de alto risco, como medicina, carros autônomos ou concessão de crédito. Nessas áreas, além da previsão, estamos frequentemente interessados no grau de certeza do modelo para que, caso ele seja muito alto, possamos passar a decisão para um especialista humano.

Intuição

De uma forma bastante simplista, podemos entender Processos Gaussianos como um interpolador de dados. Assumindo que não há ruído, um interpolador prevê sempre o valor observado onde há dados. A parte complicada então é saber o que prever entre um e outro ponto. A intuição diz que nossas previsões não mudam bruscamente se as variáveis explicativas não mudarem muito. Por exemplo, se eu observo \(y=0\) quando \(x=0\) então devo esperar que \(y\) seja próximo de zero quando \(x\) por próximo de zero, digamos \(x=0.1\). Na imagem abaixo podemos ver como Processos Gaussianos estão de acordo com essa intuição e fazem uma interpolação bastante elegante.

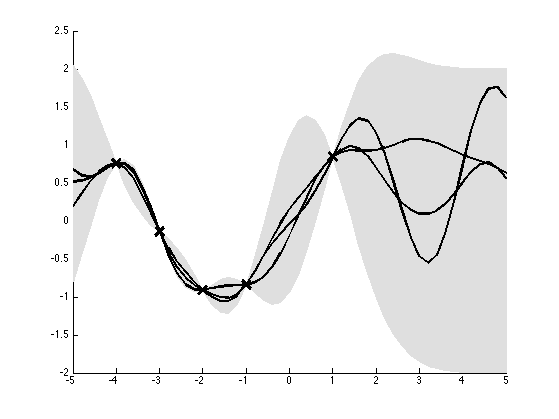
A imagem mostra 3 amostras de um processo gaussiano definido pelas 5 observações marcadas com x. Note que, onde há dados, o valor previsto é o mesmo que o observado e não há incerteza (lembre-se de que assumimos ruído zero). Conforme nos afastamos dos dados, a incerteza da interpolação aumenta, denotada pelo alargamento do intervalo de confiança de 95% (em cinza).

Então, recapitulando, se podemos entender Processos Gaussianos como uma espécie de interpolador, que, de quebra nos dá informações de incerteza, precisamos que ele defina duas coisas: uma noção de distância ou similaridade e uma noção de variância. Para entender isso melhor, precisaremos entrar um pouco na matemática

Matemática

Kernel

A noção de distância entre dois pontos é definida num Processo Gaussiano pelo que chamamos de kernel, uma função de dois pontos no espaço, geralmente não linear, que pode ser interpretada como a distância entre os seus pontos de entrada. Um kernel bastante popular é o exponencial quadrático, também conhecido como função de base radial ou kernel gaussiano:

\[k(x,x') = \sigma^2 exp\Bigg(-\frac{(x-x')^2}{2\mathcal{l}^2}\Bigg)\]

Ele tem esses nomes pois é igual a função gaussiana, tirando o fator de normalização. Isso lhe confere algumas propriedades de distância bastante interessantes. Ele pode ser entendido como uma função gaussiana onde x é o ponto de máximo e distância aumenta conforme nos afastamos desse ponto. O hyper-parâmetro \(\mathcal{l}\) é como se fosse a variância dessa gaussiana, controlando quão larga é a curva. Dessa forma, \(\mathcal{l}\) muito pequeno nos diz que a distância aumenta rapidamente quando nos afastamos de x e, por conseguinte, espera-se que a nossa função interpoladora varie muito e rapidamente, sendo pouco suave. Um \(\mathcal{l}\) grande, por sua vez, introduz uma noção de distância que diminui lentamente conforme nos afastamos de x e, por conseguinte, a função interpoladora será mais suave.

Já o fator de dimensionamento \(\sigma^2\) tem uma interpretação mais simples: eles nos diz o quanto esperamos que nossa distância seja algo fora da média (zero, na imagem abaixo).

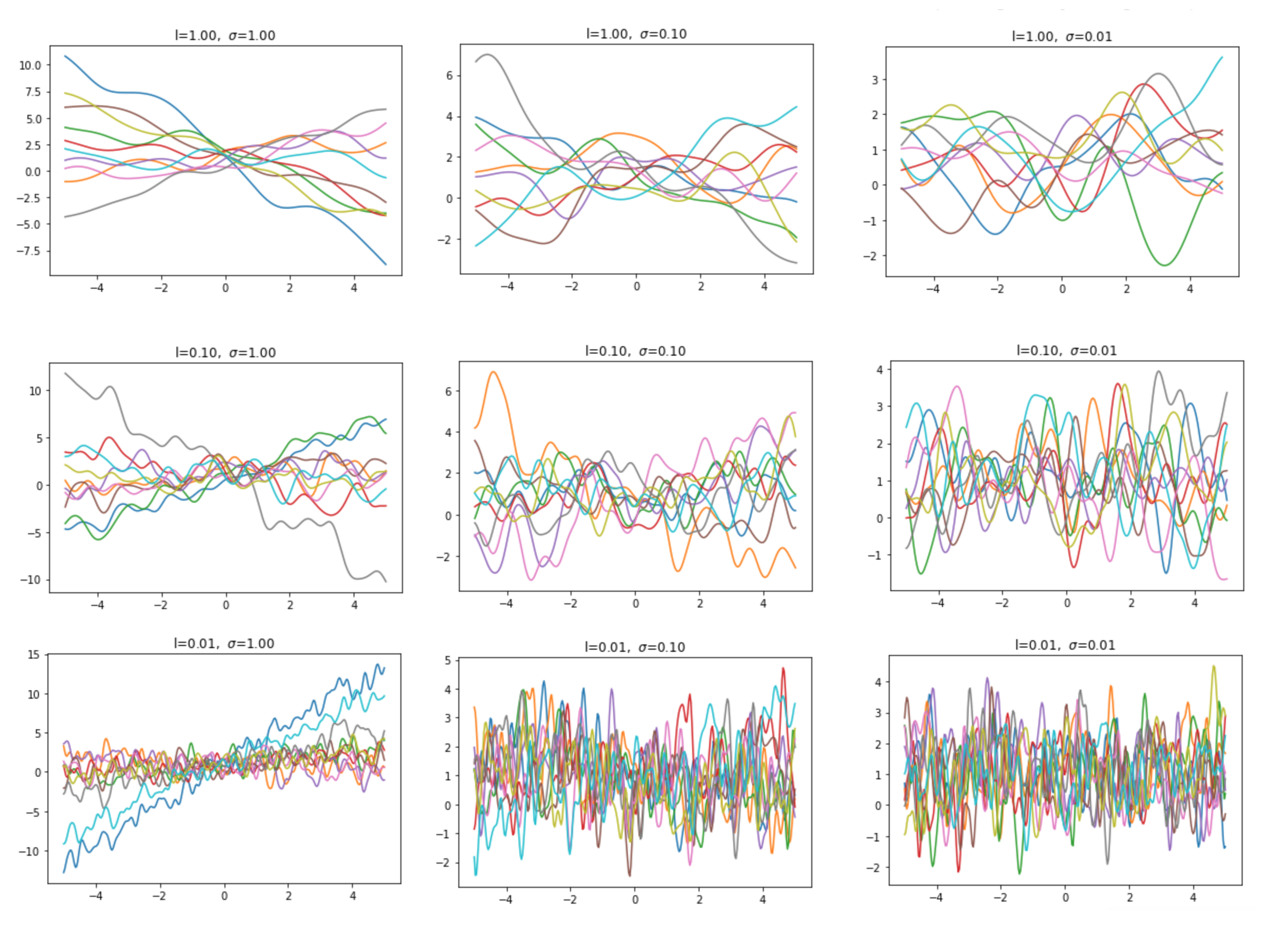
Claro que existem muitos outros kerneis além do gaussiano, mas falar sobre eles não é o propósito deste post. Caso queira saber mais, confira o Kernel cookbook, com alguns exemplos de kernels e suas aplicações. Por hora, o que é importante ter em mente é que o kernel é uma função que pode ser interpretada como a distância ou similaridade entre dois pontos.

Matriz de Covariância

Outra coisa que carrega uma noção de distância são matrizes de covariância. Caso não lembre muito sobre matriz de covariância, pegue um DataFrame qualquer no Pandas e use df.cov().

Intuitivamente, a matriz de covariância nos diz como cada uma das variáveis são parecidas entre si (ou linearmente dependentes). Isso porque a uma boa parte da operação de covariância é simplesmente computar a produto interno entre duas colunas, que nada mais é do que a noção mais simples que há de distância. Como exemplo, considere os dados diários de aluguel de Bike.

import pandas as pd # pada DataFrames
import numpy as np # para computação numérica
from toolz.curried import * # para programação funcional

data = pipe("/Users/matheusfacure/Downloads/Bike-Sharing-Dataset/day.csv", 
            pd.read_csv,
            lambda df: df[["instant", "season", "workingday", "weathersit", "temp", "hum", "windspeed", "cnt"]])
            

pipe(data,
     lambda df: (df - df.mean()) / df.std(),
     lambda df: df.cov())            

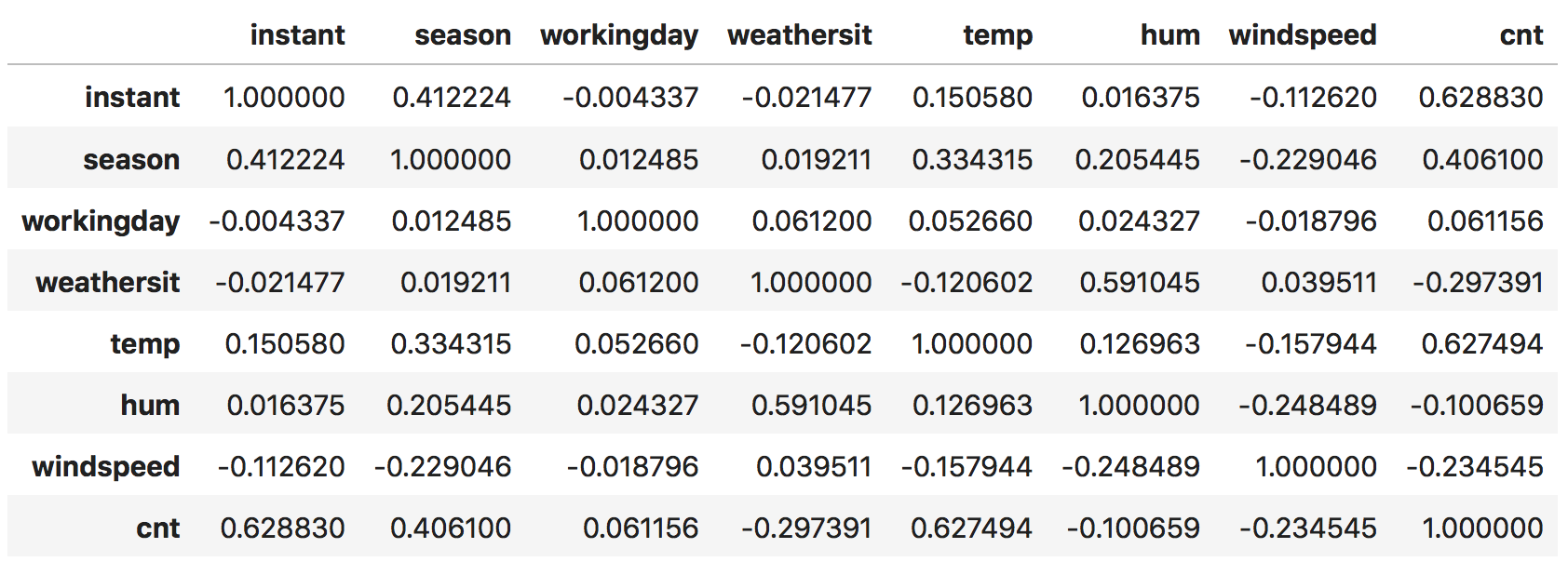
No exemplo acima, podemos ver que a quantidade de ciclistas (cnt) está bastante correlacionada com a estação do ano (season). De certa forma, isso quer dizer que esses duas colunas estão próximas umas das outras, já quem ter informações sobre uma nos diz muito sobre a outra.

Apenas por diversão, para ver mesmo que covariância nada mais de do que um produto interno (mais uma pequena normalização), você pode conseguir os mesmo resultado acima da seguinte forma

pipe(data,
     lambda df: (df - df.mean()) / df.std(),
     lambda df: df.T.dot(df) / 730) # 730 é o fator normalizador

Estou mostrando isso porque não é possível ressaltar o suficiente que covariância é uma métrica de similaridade, assim como produtos internos. Guarde bem isso na sua cabeça que Processos Gaussianos se tornarão algo simples.

Agora, e se, em vez de usar a covariância tradicional de uma base de dados, a gente antes virasse a tabela? Nesse caso a matriz covariância obtida seria \(N\)x\(N\) e nos daria informações sobre o quão similares são as observações entre si!

pipe(data.T, # inverte linhas e colunas
     lambda df: (df - df.mean()) / df.std(),
     lambda df: df.cov())

Isso parece exatamente o que precisamos num interpolador, isto é, uma noção de distância entre as amostras para prever coisas parecidas para observações também parecidas.

Uma outra ideia é que usar um simples produto interno na hora de computar a covariância talvez não seja a melhor coisa que possamos fazer. E se quisermos usar uma distância não linear? Para isso, podemos substituir o produto interno por uma função kernel, que também codifica distância, mas numa forma muito mais flexível e complexa.

Processo Gaussiano

Vimos que kerneis e matriz de covariância são formas de representar uma noção de distância, que é o que precisamos para criar um bom interpolador. Agora podemos juntar tudo isso que vimos para entender os Processos Gaussianos.

Uma coisa bastante surpreendente sobre processos gaussianos é que eles são absurdamente fáceis de implementar, pois não passam de distribuições Gaussianas Multivariadas. Só precisamos definir uma média e uma covariância que teremos nosso GP. Por outro lado, embora fácil, conseguir essa média e covariância envolve bastante teoria de álgebra linear e de distribuições gaussianas. Se você não souber toda essa teoria de cara, não se preocupe pois toda ela está facilmente disponível na internet (por exemplo na Wikipédia) e você só precisa copiar e colar algumas operações algébricas para código.

Formalmente, uma função \(\pmb{f}\) é um Processos Gaussianos se qualquer conjunto finito \( \{ \pmb{f}(\pmb{x}_1), \pmb{f}(\pmb{x}_2), …, \pmb{f}(\pmb{x}_n) \} \) segue uma distribuição normal multivariada, onde \(\pmb{x}\) tipicamente representam um vetor observação (linha) numa tabela de dados. Assim como uma gaussiana, um GP é definido por uma função de média \(\pmb{m(x)}\), que é usualmente assumida como zero. Além disso, um PG é definido por uma função de covariância \(k(\boldsymbol x, \boldsymbol x’)\), também conhecida por kernel. A função de covariância é usada para construir uma matriz de covariância \(N\)x\(N\). Juntando isso, podemos retirar amostras a priori de um GP com

\[\boldsymbol f \sim \mathcal N(\boldsymbol m_{\boldsymbol X}, \boldsymbol K_{\boldsymbol X \boldsymbol X})\]

Em que \(\pmb{m}\) é da mesma dimensão de \(\pmb{X}\) e \(K\) tem dimensões \(XX^T\). Geralmente assumimos que \(\pmb{m}\) é zero. Isso se traduz para algumas poucas linhas de código Python.

def kernel(A, B, l=0.1, sigma=0.1):
    sqdist = np.sum(A**2,1).reshape(-1,1) + np.sum(B**2,1) - 2*np.dot(A, B.T)
    return np.exp(-.5 * (1/l) * sqdist) + sigma * np.kron(A,B.T)
    
plot_xs = np.reshape(np.linspace(-5, 5, 300), (300,1))
K_xx = kernel(plot_xs, plot_xs, l=1, sigma=1)
f_prior = np.random.multivariate_normal(np.zeros(len(plot_xs)), K_xx, size=10).T

A única coisa que talvez não seja muito obvia acima é np.kron(A,B.T), que é simplesmente a função Delta Kronecker. Apesar do nome pomposo, ela nada mais é do que uma forma de ver se duas coisas são iguais, retornando 1 se sim e 0 c.c..

Algo muito conveniente sobre distribuições gaussianas é que é possível obter a distribuição condicional a partir da distribuição conjunta de maneira bastante simples. Digamos que você tenha dados de treino \(\pmb{X}\) e \(\pmb{f}=\pmb{y}\) e queria prever para um dado de teste \(\boldsymbol X_*\) a variável resposta \(\boldsymbol f_* = y_*\). Você pode concatenar essas peças em uma gaussiana da seguinte forma.

\[\begin{pmatrix} \boldsymbol y \\ \boldsymbol y_* \end{pmatrix} \sim \mathcal N \left( \begin{pmatrix} \boldsymbol 0 \\ \boldsymbol 0 \end{pmatrix}, \left(\begin{matrix} \boldsymbol K \\\boldsymbol K_{*}\end{matrix} \begin{matrix} \boldsymbol K_{*}^T \\ \boldsymbol K_{**}\end{matrix}\right)\right).\]

Note que \(\boldsymbol K\) é a matriz covariância obtida ao aplicar o kernel em \(\boldsymbol X\) com \(\boldsymbol X\), \(\boldsymbol K_*\) é obtida aplicando o kernel em \(\boldsymbol X\) com \(\boldsymbol X_*\) e \(\boldsymbol K_{**}\) é obtida aplicando o kernel em \(\boldsymbol X_*\) com \(\boldsymbol X_*\). Com isso, podemos sair da distribuição conjunta acima para a distribuição condicional, mostrada abaixo.

\[p(\boldsymbol y_*\vert \boldsymbol X_*, \boldsymbol X, \boldsymbol y) = \mathcal N(\boldsymbol K_{*} \boldsymbol K^{-1}\boldsymbol y, \boldsymbol K_{**} - \boldsymbol K_{*} \boldsymbol K^{-1} \boldsymbol K_{*}).\]

Provar esse resultado envolve bastante matemática e não é o propósito deste post. Você pode achar várias provas desse teorema online, como por exemplo essa aqui no StackExchange.

Código

Antes de qualquer coisa, como vamos trabalhar com as matrizes de covariância obtidas a partir do kernel, precisamos obtê-las dos dados de treino e teste.

K_xx = kernel(X_test, X_test, l, sigma_y)
K_ss = kernel(X_train, X_train, l, sigma_y)
K_sx = kernel(X_train, X_test, l, sigma_y)

Olhando a fórmula acima podemos notar a inversão de \(\boldsymbol K\), uma matriz NxN. Por questões de instabilidade numérica, implementar a formula acima não é muito recomendado. Por isso, usamos algo chamado de Decomposição de Cholesky, que pode ser entendido como uma espécie de raiz quadrada para matrizes. Assim, se \(\boldsymbol K = \boldsymbol L^T \boldsymbol L \), então \(\boldsymbol L = \texttt{Cholesky}(\boldsymbol K)\). O algoritmo final pode ser descrito nas seguintes linhas

\[\boldsymbol L = cholesky(\boldsymbol K + \boldsymbol \sigma_n^2 I) \\ \boldsymbol \alpha = \boldsymbol L^T \texttt{\\} \boldsymbol L \texttt{\\} \boldsymbol y \\ \mathbb{E}[\boldsymbol y_*] = \boldsymbol K_*^T \boldsymbol \alpha \\ \boldsymbol v = \boldsymbol L \texttt{\\} \boldsymbol K_* \\ Var [\boldsymbol y_*] = \boldsymbol K_{**} - \boldsymbol v^T \boldsymbol v\]

Que se traduz para as seguintes linhas de código Python

L = np.linalg.cholesky(K_xx + sigma_y*np.eye(len(X_train)))
alpha = np.linalg.solve(L.T, np.linalg.solve(L, y_train))
mu = K_sx.T.dot(alpha).squeeze()

v = np.linalg.solve(L, K_sx)
cov = K_ss - v.T.dot(v)

Com a média e covariância, podemos retirar amostrar do nosso Processo Gaussiano e até plotá-las com um intervalo de confiança.

np.random.seed(42)
f_post = np.random.multivariate_normal(mu, cov, size=10).T
stdv = np.sqrt(np.diagonal(cov))

plt.plot(X_test, f_post)
plt.gca().fill_between(X_test.flat, mu-2*stdv, mu+2*stdv, color="#dddddd")
plt.title('Amostras A Posteriori de um Processo Gaussiano')
plt.plot(X_train, y_train, 'bs', ms=8)
plt.show()

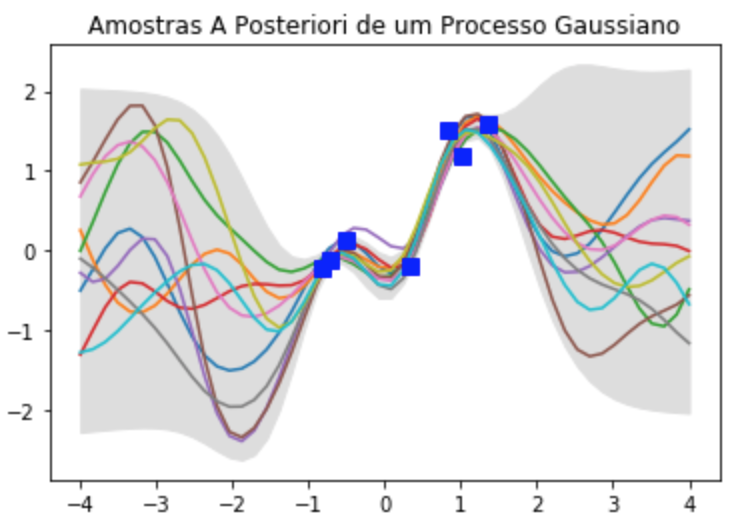
Além de bonita, essa imagem mostra como o GP capta bem a intuição bayesiana de colocar mais incerteza onde há menos dados.

Referências

Este tutorial foi amplamente inspirado na aula de Processos Gaussianos do professor Nando de Freitas, bem como nas suas notas de aula. Cada aula de Nando é uma pérola e recomendo fortemente que você assista todo o seu curso de Aprendizado de Máquina, lecionado na University of British Columbia.

Além disso, muitas ideas foram tiradas do tutorial sobre Processos Gaussianos de Keyon Vafa, e do tutorial Gaussian Processes for Dummies, de Katherine Bailey.

Caso queria se aprofundar mais no assunto, sugiro que comece com o artigo de M. Ebden, Gaussian Processes for Regression: A Quick Introduction. Por fim, recomendo o livro de Kevin P. Murphy, Machine Learning: A Probabilistic Perspective

Como de costume, o código deste tutorial está disponível no meu GitHub.