Modelos Lineares Generalizados

Existem situações ao se fazer uma modelagem que o objeto de estudo central não é uma variável quantitativa, impossibilitando a tradicional regressão linear. Para solucionar esse problema, os modelos lineares generalizados surgiram para contornar esse problema e utilizam distribuições que são da família exponencial e possuem determinadas propriedades em comum. Um caso particular dessa família é a distribuição normal, por isso o nome de generalizado.

Existem várias aplicações, mas basicamente existem 3 grandes subgrupos de aplicações:

O primeiro são dados de contagens, como número de carros que passam em uma rodovia a cada minuto, número de homicídios por dia em determinada cidade e número de reclamações de uma determinada seguradora por cliente;
O segundo grupo são para dados categóricos que são os mais conhecidos, algumas aplicações são as transações bacárias fraudulentas, uso ou não de um seguro de carro durante o período contratado, a oscilação positiva ou negativa de uma ação;
O terceiro grupo, menos conhecido, são dados assimétricos positivos, uma aplicação seria dados de precipitação ou temperatura de determinada cidade.

Dividiremos o post nas seguintes etapas: (1) explicaremos os modelos mais comuns em MLG; (2) aplicabilidade em um problema de contagem, utilizando uma base real.

Modelagem

Os modelos lineares generalizados (mlg) são uma classe de modelos que aumentam as possibilidades de análises para outras distribuições que não seja apenas a distribuição normal, portanto a regressão linear tradicional é um caso particular de MLG, esse fato será discutido mais a frente. Os MLGs são utilizados quando o objetivo do estudo é fazer uma análise sobre uma variável resposta que seja principalmente uma:

Contagem;
Categórica;
Assimetria (com valores positivos).

Uma abordagem sobre esse tema já foi introduzido no post do Cayan Portela (Modelo Tweedie Poisson Compound para dados de sinistros de veículos), é recomendada a leitura para compreender uma outra extensão desses modelos.

Por definição, para ser um MLG é necessário que a distribuição de probabilidade seja da família exponencial (abordaremos apenas a família exponencial unidimensional, um parâmetro apenas), ou seja, a distribuição pertence a uma classe de distribuições que possuam alguns aspectos em comum, como: satisfazem o lema da fatoração de neyman (estatística suficiente), possuam estatística suf. minimal, média \((\bar{x})\) é suficiente, possa ser escrita no seguinte formato:

\[f(y_i;\theta_i,\phi) = \mbox{exp}\left\{\phi^{-1} [y_i a(\theta_i) - b(\theta_i)] + c(y_i,\phi)\right\}\]

No qual, \(\theta\) é o parâmetro do modelo, \(y\) os dados observados e \(\phi\) um parâmetro de dispersão, que pode ser unitário em casos de distribuições que não possuem ele explicitamente (Poisson é um exemplo). A família exponencial é muito importante porque possui características comuns a várias distribuições famosas como Normal, Poisson, Exponencial, Binomial, Gama, Normal Inversa, Binomial Negativa. Além disso, é chamada de familia exponencial canônica quando a função \(a(\theta_i) = \theta_i\) não ocorre naturalmente, mas pode ser feita uma reparametrização.

Duas propriedades muito importantes dos MLG’s é a relação que a função \(b(\theta_i)\) possui com a média e variância dos dados. \(E(Y_i) = b'(\theta_i) = {\mu_i}\)

\[Var(Y_i) = \phi b''(\theta_i) = \phi V(\mu_i)\]

No qual \(b’\) e \(b’’\) se referem a primeira e segunda derivada em relação ao parâmetro \(\theta_i\). Note que o parâmetro de dispersão possui um papel importante na variância, podendo inflar a variância dos dados caso seja necessário e, caso não seja, ocorre a equivalência das variâncias indicando que a variância do próprio modelo já consegue capturar toda a dispersão.

No caso da regressão, os MLG’s possuem a seguinte forma:

\[g(\boldsymbol{\mu_i}) = \boldsymbol{x_i\beta_i}\]

No qual, \(\beta_i\) são os coeficientes do modelo, \(x_i\) as observações e a função g é chamada de função de ligação, quando \(\theta_i = g(\mu_i)\) dizemos que \(g\) é a ligação canônica. Um caso particular é quando consideramos a função \(g\) como identidade e a distribuição normal com média e variância desconhecida, dessa forma obtemos o equivalente a regressão linear comum e os métodos de estimação coincidem.

Outro fato relevante é que não existe explicitamente na construção um termo de erro, isso não quer dizer que o modelo não possui erro, apenas que o termo não é nítido como na regressão linear. Em MLG ainda é necessário análise de resíduos para verificar o ajuste e qualidade do modelo.

Na prática, existem alguns modelos considerados baseline e alguns candidatos que podem ter ajuste melhor, além de alguns fatos estilizados conforme cada categoria do MLG listada anteriormente. Cada categoria será análisada a seguir e indicado um roteiro de possíveis variações.

Contagem

Para dados de contagem, o modelo principal se baseia na distribuição de poisson (na forma canônica \(\theta_i = log(\mu_i)\)). Ele tem a carácterística de que \(E(Y_i) = Var(Y_i) = \mu_i\), ou seja, a média é igual a variância, conhecido como equidispersão. As ligações mais comuns são logaritmica, raiz e identidade.

Portanto, em situações em que os dados possuem muita variabilidade e é esperado que a igualdade não seja atendida pode ser interessante ajustar modelos que levam isso em consideração. A primeira opção seria o modelo Poisson com disperssão, Poi(\(\mu_i\),\(\phi\)), que insere o parâmetro para capturar a variabilidade. Outra opção, é o modelo Binomial Negativo (com ou sem parâmetro de dispersão) que pela definição não é MLG mas possui características muito semelhantes e possui uma boa capacidade de capturar um efeito \(E(Y_i) < Var(Y_i)\) e além disso consegue, de certa forma, lidar bem com um problema chamado de inflação de zeros que é exatamente uma alta frequência de contagens 0. Outros modelos que podem trabalhar a inflação de zeros são poisson inflacionada de zeros (ZIP), binomial negativa inflacionada de zeros (ZINB) e modelos com barreira (hurdle).

De forma sucinta, para dados de contagem é necessário observar o excesso de zeros e a dispersão. Dessa forma temos a seguinte sugestão de modelos.

Sem excesso de zeros e sem dispersão: Poisson;
Sem excesso de zeros e com dispersão: Poisson com dispersão e Binomial negativa sem/com dispersão;
Com excesso de zeros e sem dispersão: Binomial negativa sem/com dispersão, ZIP, ZINB e hurdle.

Categórica

Para dados categóricos, o modelo principal se baseia na distribuição binomial, o que fornece a regressão logística.Possui a característica de estimar facilmente a razão de chances, uma medida importante e comumente utilizada para mensurar efeitos das variáveis. As ligações mais comuns nessa classe de MLG são logaritmica, exponencial, identidade, normal acumulada e log log complementar.

Geralmente, os modelos são utilizados quando a variável categórica possui apenas duas categorias, mas possuem adaptações para quando possuem 3 ou mais. Quando são mais de duas categorias, é necessário verificar se a relação entre as categorias é nominal (dias da semana por exemplo) ou ordinal (opinião de um filme: gostou, indiferente, não gostou), ou seja, se as categorias possuem ou não uma relação de intensidade. Caso não exista essa relação de intensidade a regressão logística nominal pode ser utilizada e, caso exista, a regressão logística ordinal.

Como já mencionado, para estimar a razão de chance o modelo mais recomendado é a regressão logística, mas isso não impede que outros modelos possam estimar também, mas nesse modelo o resultado é obtido imediatamente exponenciando os coeficientes \(\beta_i\) do modelo. Para se estimar o risco relativo que é outra medida muito utilizada, é usualmente ajustado o modelo log-binomial. Outras medidas como risco absoluto e dose letal podem ser obtidas usando o mesmo modelo binomial mas com ligação identidade e a acumulada da normal (F).

Assimétria (com valores positivos)

Modelos para dados assimétricos positivos podem ser modelados por regressão linear caso a assimetria não seja acentuada. O modelo mais usado para esse tipo de dado é o modelo gama, que possui uma distribuição muito flexível para ajuste. As ligações mais comuns são identidade, inversa e logaritmica. Caso existam muitos outliers, o modelo com a normal invertida é uma sugestão para melhorar o ajuste. A regressão Skew-Normal também é competitiva com as demais modelagens, mas possui a vantagem de aceitar dados negativos e também uma flexibilidade para ajuste.

Essa classe de modelo é menos conhecida e estudada, uma vez que para corrigir a assimetria são feitas transformações como a logaritmica para normalizar os dados e efetuar a regressão linear. Independente da abordagem, é necessário verificar os objetivos da análise e qual modelo consegue de forma mais efetiva cumpri-los.

Banco de dados

O banco de dados utilizado será o mesmo do post feito pelo Cayan sobre o Tweedie-Poisson. Os dados referem-se ao número de sinistros e total de pagamento (valores monetários) gerados, por grupo e número de reclamções que será o objetivo da modelagem nesse post.

O número de reclamações (Claims) é uma variável de contagem que representa quantas reclamações foram feitas. Portanto, o valor 0 significa que não ocorreu reclamação e é algo que pode influenciar na análise como mencionado nos fatos estilizados de modelos de contagem. Além disso, o número de reclamação assume valores elevados, entretanto foi feito um corte na base de dados para permanecer apenas as observações que tiverem no máximo 20 reclamações, uma vez que os valores acima disso são escassos e não possuem tanta relevância no estudo.

Considerando que o objetivo é modelar o número de reclamações, os modelos de contagens são os mais indicados. Portanto, serão analisados 4 modelos (mencionados na seção anterior) como propostas e verificados seu ajuste e erro. Para verificar a qualidade do modelo, foi utilizado o gráfico QQ-norm para verificar a normalidade dos resíduos, distância de Cook para observar a existência de valores influentes no modelo e o gráfico Rootograma que é um gráfico que é semelhante ao histograma mas “pendura” as barras do histograma no valor observado de forma que fica visualmente mais explicito a distância do valor ajustado e observado. Todos esses conceitos serão melhor compreendidos no decorrer da análise.

Análise de dados

Para a análise foi utilizado o banco de dados de sinistros de automóveis na Suécia, no ano de 1977, utilizando o ambiente R de computação estatística.

A base de dados pode ser obtida no link a seguir: StatiSci. A descrição das variáveis está disponível no link.

Primeiramente, serão lidos os dados, uma filtragem para manter apenas reclamações inferiores ou iguais a 20 e o histograma da variável resposta de interesse.

library(dplyr)
library(MASS)
library(pscl)
library(vcd)
dados <- read.table("http://www.statsci.org/data/general/motorins.txt", sep = "\t", head = TRUE) 
dados$Make <- as.factor(dados$Make)

dados <- dados %>% filter( Claims <= 20 ) # 1622 observações, 74% da base original

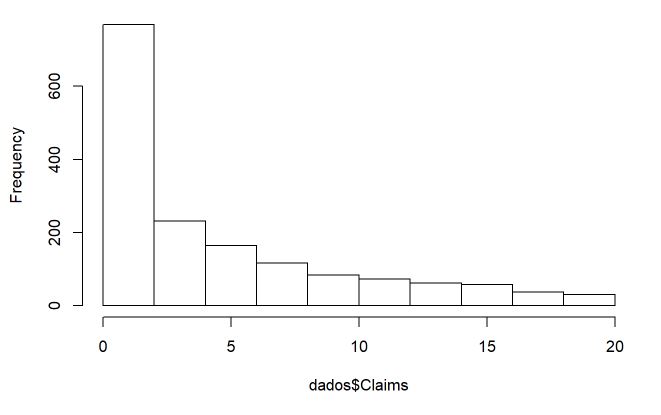
hist(dados$Claims)
sum(dados$Claims==0)/nrow(dados)

Pelo histograma, verifica-se uma quantidade consideravel de contagens baixas, o que pode ser um indício que modelos que possuem a característica de zeros inflados possam ter vantagem (23% das observações possuem contagem 0).

Modelagem

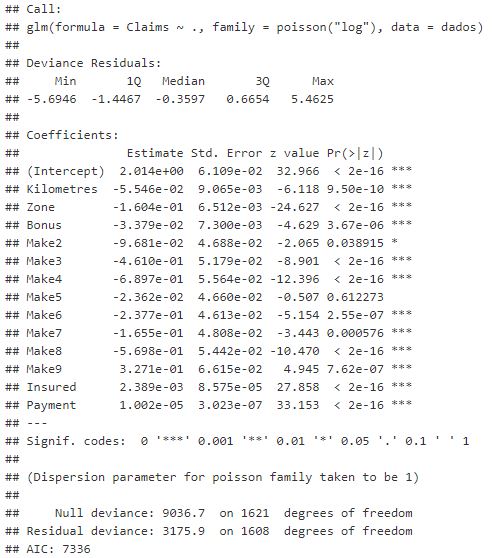
Como mencionado, o modelo benchmark inicial pela sua simplicidade e aceitação na literatura é o modelo Poisson. Observando as estimativas do modelo ajustado, é verificado que as variáveis são significativas em sua maioria e seus coeficientes muito pequenos, isso se deve a magnitude de algumas variáveis como Payment.

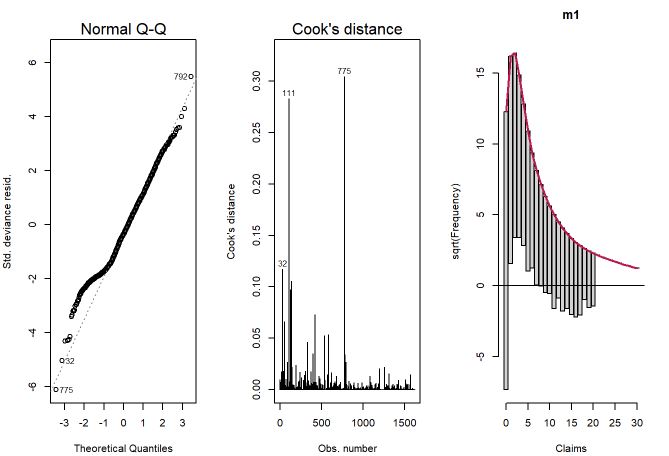
Ao analisar os gráficos, primeiramente se tem o gráfico QQplot que representa o ajuste dos resíduos do modelo em uma distribuição normal, ou seja, os quantis empíricos dos resíduos são comparados com os quantis teóricos de uma distribuição normal, quanto mais próximo for essa comparação teremos uma reta linear perfeita indicando que o quantil teórico e empirico são iguais, conforme ocorre uma distorção nessa reta existem indícios de que nessa região os resíduos empíricos ‘fogem’ da distribuição teórica. O segundo gráfico remete a distância de Cook para cada observação da amostra, essa distância é uma medida baseada na matriz hessiana (H, hat) levando em consideração a informação de fisher, conforme aumenta essa distância a influência de alguma observação sobre o modelo é grande, indicando que seus coeficientes podem estar estimados de forma equivocada e ter grande variabilidade ao mudar a base de dados. Para valores acima de 0,5 a distância é considerada como ‘alta’, esse valor é muito utilizado na literatura mas sem um rigor matemático para definição.

A partir desse esclarecimento sobre os gráficos, percebe-se uma cauda um pouco pesada no QQplot, mas não distorcendo muito do ideal (ser uma reta linear), além disso não existem observações que sejam influentes nos parâmetros porque a distância de Cook é inferior a 0,5 para todas observações. Com relação ao terceiro gráfico, percebe-se que as barras das contagens mais baixas (de 0 a 5) se distanciam muito da reta das obscissas, ou seja, ocorre um resíduo maior maior nessa faixa, principalmente na contagem 0, que possui a maior discrepância. Conforme as contagens aumentam, as barras se aproximam mais do eixo x, o valor ajustado (comprimento da barra) e observado (linha vermelha) se tornam mais próximos.

m1 <- glm(Claims ~ ., family = poisson('log'), data = dados)
summary(m1)

par(mfrow=c(1,3))
plot(m1, which=c(2,4))
countreg::rootogram(m1)

Pelos gráficos do primeiro modelo, percebe-se que é necessário encontrar um modelo que consiga melhorar o ajuste. Para isso, a distribuição binomial negativa deve conseguir ajustar melhor pela sua capacidade de captar sobredispersão e também, de certa forma, a inflação dos zeros, mas antes disso ajustaremos a Poisson com dispersão.

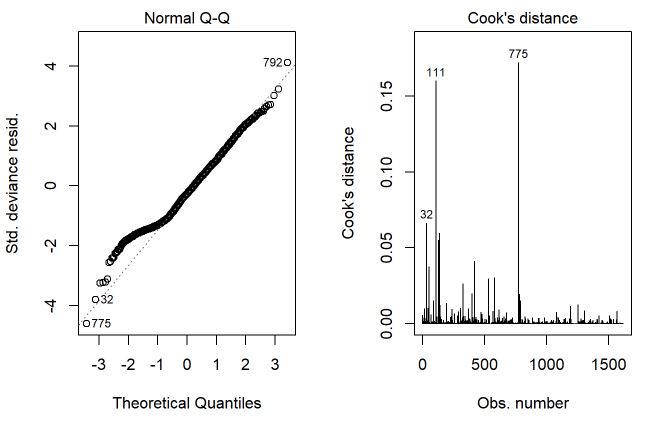
Ao observarmos os gráficos, verificamos uma diminuição das distâncias de cook e uma leve melhora no QQplot. O gráfico rootograma não foi ajustado por conta da incompatibilidade dos pacotes

m2 <- update(m1, family=quasi(link='log', variance='mu'))
summary(m2)

par(mfrow=c(1,2))
plot(m2, which=c(2,4))

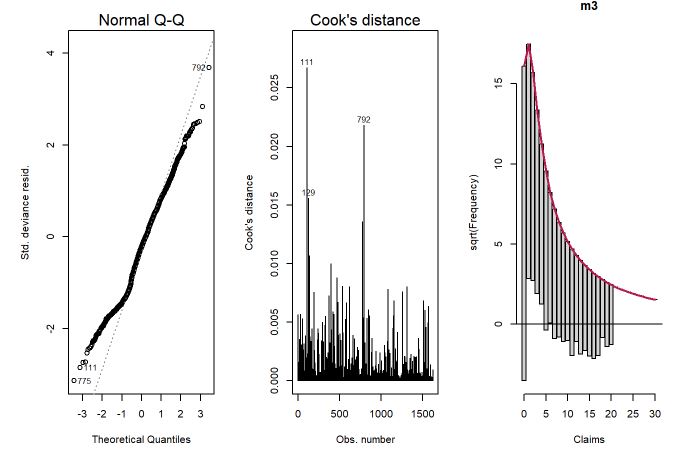
Ajustando o modelo binomial negativo, percebe-se novamente uma melhora nos 3 gráficos. As contagens mais baixas que não tiveram um ajuste muito bom melhoraram o ajuste no modelo binomial negativo. O ajuste no 0 também melhorou, mas ainda será ajustado o modelo binomial negativo com inflação no zero para verificar se melhora o ajuste. O QQplot também teve uma melhora na cauda (exatamente por conta do ajuste melhor) e a distância de Cook reduziu novamente, mostrando que as observações individualmente não influenciam erroneamente o modelo.

m3 <- glm.nb(Claims ~ ., data=dados)
#summary(m3)

par(mfrow=c(1,3))
plot(m3, which=c(2,4))
countreg::rootogram(m3)

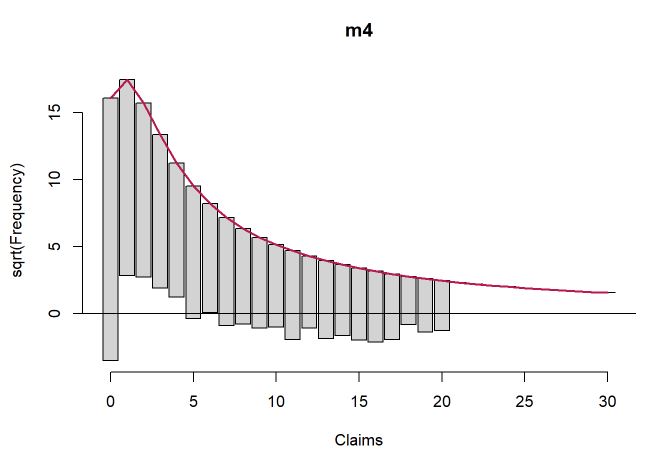
Para finalizar, foi ajustado o modelo binomial negativo com inflação nos zeros. Os modelos com inflação no zero colocam uma massa pontual específica no zero, ou seja, uma mistura que assume um modelo específico para o zero e outro modelo para as demais contagens. Mais uma vez os ajustes melhoraram e, especialmente na contagem 0, melhorou a estimativa.

Colocando o erro quadrático médio (EQM) como medida de comparação dos modelos, percebe-se uma redução do EQM conforme aumenta a complexidade do modelo. Portanto, o modelo com menor EQM é o binomial negativo com inflação nos zeros seguido pelo binimoial negativo sem inflação, ambos são bons candidatos, a definição final de qual seria o escolhido seria um trade off entre facilidade de interpretação (no modelo com inflação são dois modelos em 1) e erro.

m4 <- zeroinfl( Claims ~  . | 1, dist="negbin", data = dados)
#summary(m4)

par(mfrow=c(1,1))
countreg::rootogram(m4)


cat(" Poisson EQM                  :",mean(residuals(m1)^2),'\n',
    "Poisson Dispersão EQM        :",mean(residuals(m2)^2),'\n',
    "Binomial Negativa EQM        :",mean(residuals(m3)^2),'\n',
    "Binomial Negativa inflada EQM:",mean(residuals(m4)^2))

Não foi feita uma seleção de variáveis e outras análises pertinentes como validação de um possível modelo final pois o objetivo era expor o conhecimento e modo de usar de cada um, mas são etapas muito importantes e imprescindíveis de uma boa modelagem.

Referências

Dobson, Annette J., 1945- An introduction to generalized linear models / Annette J. Dobson and Adrian G. Barnett. – 3rd ed.

Gilberto A. Paula, MODELOS DE REGRESSÃO com apoio computacional.Instituto de Matemática e Estatística Universidade de São Paulo.