Diagnóstico em Regressão

Existem situações ao se fazer uma modelagem que o objeto de estudo é a interpretabilidade do modelo, impossibilitando modelos como Suport Vector Machine, Redes Neurais e outros. Para solucionar esse problema, os modelos estatísticos tradicionais como regressão linear e modelos lineares generalizados conseguem captar o efeito das variáveis explicativas sobre a variável resposta. Contudo, cada um desses modelos possui seus pressupostos específicos e para que se possa fazer inferência nos resultados, é necessário que os pressupostos estejam sendo respeitados. Esse post tem como objetivo ensinar técnicas que vão além de retirar valores discrepantes detectados pelo boxplot (acima (abaixo) de 1,5 x 3°(1°) quartil) para melhorar o ajuste de um modelo.

Existem métodos gráficos e testes estatísticos para diagnóstico. Esses métodos tentam identificar basicamente:

Outliers, Valores influentes, Pontos de alavanca
Normalidade (ou outra distribuição que seja considerada nos pressupostos)
Homocedasticidade (variância constante)
Outros pressupostos que variam conforme o modelo

Dividiremos o post nas seguintes etapas: (1) explicaremos as técnicas mais utilizadas, sua importância, interpretação e quando deve ser utilizada; (2) aplicabilidade em um problema de regressão, utilizando uma base real do próprio software R (Iris).

Diagnóstico

Métodos de diagnóstico são utilizados para que desvios entre as observações e os valores ajustados do modelo sejam analisados e verificados o seu grau de influência sobre a análise.

Essa diferênça entre o real e o previsto podem surgir por vários motivos, pela função de variância, função de ligação, ausência ou não parâmetro de dispersão, parâmetro de inflação nos zeros, ou ainda pela definição errada da escala da variável ou mesmo porque algumas observações se mostram dependentes ou possuem correlação serial. Discrepâncias pontuais podem ocorrer porque as observações estão nos limites observáveis da variável, erros de digitação, algum fator não controlado (mas relevante) influenciou a sua obtenção ou até mesmo multicolinearidade entre variáveis (correlação alta entre variáveis).

As técnicas de diagnóstico podem ser formais ou informais. As informais baseiam-se em gráficos para detectar padrões visualmente e ver o comportamento dos dados. As formais envolvem especificar o modelo sob pesquisa em uma e verificar via testes, intervalos de confiança e outras medidas específicas para cada modelo, as mais usadas são baseadas nos testes da razão de verossimilhanças e escore.

Esse post terá como foco o modelo de regressão linear na apresentação de fórmulas por simplicidade, a extensão do conteúdo acontece de forma natural para modelos lineares generalizados e outras classes de modelo acrescentando os parâmetros pertinentes.

No modelo de regressão linear, que tem forma \(Y=X\beta + e\), os elementos \(e_i\) do vetor e são as diferenças entre os valores observados y_i e aqueles esperados \mu_i pelo modelo. Essa diferença é chamada de resíduo e considera-se como pressuposto do modelo que os resíduos sejam independentes e que tenham distribuição normal (a distribuição esperada pode mudar conforme o modelo), cabe ressaltar que a normalidade deve ser verificada nos resíduos e não na variável resposta Y.

Os resíduos indicam a variação natural dos dados, um fator aleatório (ou não) que o modelo não capturou. Se as pressuposições do modelo são violadas, a análise será levada a resultados duvidosos e não confiáveis para inferência. Essas falhas do modelo nos pressupostos podem ser oriundas de diversos fatores como não linearidade, não-normalidade, heterocedasticidade, não-independência e isso pode ser causado por pontos atípicos (observações discrepantes), que podem influenciar, ou não, no ajuste do modelo.

Depois de ajustado um modelo algumas medidas básicas de pressuposições sempre devem ser verificadas como

valores estimados (ou ajustados) \(\hat{\mu}_i\);
Resíduos ordinários \(r_i = y_i - \hat{\mu}_i\) (existem outros tipos de resíduos mas partindo da mesma premissa de diferença de valores);
Variância residual estimada (ou quadrado médio residual) \(\hat{\sigma}^2 = s^2 = \sum(y_i - \hat{\mu}_i)^2/(n - p)\);
Elementos da diagonal (Leverage) da matriz de projeção \(H = X(X^TX)^{-1}X^T\)

A diagonal principal da matriz de projeção \(H = X(X^TX)^{-1}X\), em que X denota a matriz modelo, também conhecido como pontos de alavanca, que receberam esse nome por terem um peso desproporcional no próprio valor ajustado. Esses pontos em geral são remotos no subespaço gerado pelas colunas da matriz X, ou seja, têm um perfil diferente das demais observações no que diz respeito aos valores das variáveis explicativas, conforme o seu afastamento das outras observações esses pontos podem exercer forte influência nas estimativas dos coeficientes da regressão.

Agora serão apresentados algumas métricas usadas para diagnóstico de forma geral.

Resíduos

Resíduos ordinários

Os resíduos por mínimos quadrados são definidos por \(r_i = y_i - \hat{\mu}_i\). Pela definição as observações do vetor do termo de erro do modelo são independentes e têm a mesma variância, os resíduos (o erro observavel) obtidos com ajuste do modelo tem a seguinte variância

\(Var(R) = Var[(I - H)Y] = \sigma^2(I - H)\).

Os resíduos ordinários podem não ser adequados devido à heterogeneidade das variâncias e falta de independência. Então, foram construídas padronizações nos resíduos para minimizar esse problema.

Resíduos estudentizados internamente (Studentized residuals)

Um estimador não viesado para a variância dos resíduos é expresso por \(\hat{Var}(r_i) = (1 - h_{ii})s^2\) Como \(E(r_i) = E(Y_i - \hat{\mu}_i) = 0\), o resíduo estudentizado internamente (ou seja, retirando a média e dividindo pelo desvio padrão) é igual a

\[rsi_i = \frac{ri}{s \sqrt{(1 - h_{ii})}\]

Esses resíduos são mais sensíveis do que os anteriores por considerarem variâncias distintas. Ainda assim, um valor discrepante pode mudar drasticamente a variância residual dependendo do modo como se afasta da maioria das observações. Para corrigir esse problema é feita uma pequena alteração na fórmula, que será mostrada a seguir.

Resíduos estudentizados externamente (jackknifed residuals, RStudent)

Define-se o resíduo estudentizado externamente, como

\[rse_{(i)} = \frac{ri}{s_{(i)} \sqrt{(1 - h_{ii})}\]

sendo \(s^2_{(i)}\) o quadrado médio residual livre da influência da observação i, ou seja, é estimado a variância sem a observação i (por isso a ideia de Jackknife).

A vantagem de usar o resíduo \(rse_{(i)}\), além de ser mais robusto, é que, sob normalidade, tem distribuição t de Student com \((n - p - 1)\) graus de liberdade.

Pontos discrepantes

Pontos atípicos são caracterizadas por terem \(h_{ii}\) e/ou resíduos grandes, serem inconsistentes e/ou influentes. Uma observação inconsistente é aquela que se afasta da tendência geral das demais. Quando uma observação está distante das outras em termos das variáveis explicativas, ela pode ser, ou não, influente. Uma observação influente é aquela cuja omissão do conjunto de dados resulta em mudanças substanciais nas estatísticas de diagnóstico do modelo. Essa observação pode ser um outlier (observação aberrante), ou não. Uma observação pode ser influente de 3 maneiras:

Ajuste geral do modelo;
Conjunto das estimativas dos parâmetros;
Estimativa de um determinado parâmetro;

As estatísticas mais usadas para verificar pontos atípicos são:

Leverage: \(h_{ii}\) (já comentado);
\(rse_{(i)}\) (já comentado);
Influência sobre o parâmetro \(\beta_i : DFBetaS(i)\) para \(\beta_i\);
Influência geral: DFFitS(i), D(i).

Existem alguns critérios para classificação das observações como discrepantes, contudo cada autor possui o seu critério. De uma forma geral, pode-se classificar uma observação como:

Inconsistente: ponto com \( rse_{(i)} \) grande, isto é, tal que \( rse_{(i)} > t_{(1-\alpha)/(2n);n-p-1}\);
Alavanca: ponto com h_{ii} grande, isto é, tal que h_{ii} - 2p/n, no qual p é o número de parâmetros e n o tamanho da amostra. Pode ser classificado como bom, quando consistente, ou ruim, quando inconsistente;
Outlier: ponto inconsistente com leverage pequeno, ou seja, com \(rse_{(i)}\) grande e \(h_{ii}\) pequeno;
Influente: ponto com DFFitS(i), C(i), D(i) ou DFBetaS(i) grande.

Essas medidas de influência são descritas abaixo.

DFBeta e DFBetaS

São usados quando o coeficiente de regressão tem um significado prático. A estatística DFBeta(i) mede a alteração no vetor estimado \hat{\beta} ao se retirar a i-ésima observação da análise, isto é,

\[DFBeta(i) = \hat{\beta} - \hat{\beta}_{(i)} = \frac{ri}{(1 - h_{ii})}(X^TX)^{-1}x_i\]

Portanto, é possível verificar o tamanho da influência nos parâmetros que a ausência de determinada observação pode causar

DFFit e DFFitS

A estatística DFFit e sua versão estudentizada DFFitS medem a alteração no valor ajustado pela eliminação da observação i, é basicamente o DFBeta ajustado em x_i. São expressas como

\[DFFit(i) = x^T_i(\hat{\beta} - \hat{\beta}_{(i)}) = \hat{\mu}_i - \hat{\mu}_{(i)}\]

Distância de Cook

É a mais utilizada, é uma medida de afastamento do vetor de estimativas resultante da eliminação da observação i. Tem uma expressão muito semelhante ao DFFitS mas que usa como estimativa da variância residual aquela obtida com todas as n observações, considera o resíduo estudentizado internamente.

\[D_{(i)} = \frac{(\hat{\beta} - \hat{\beta}_{(i)})^T (X^TX)(\hat{\beta} - \hat{\beta}_{(i)})}{p s^2}\]

Multicolinearidade

Para finalizar, outro grande problema ocorrido nos modelos é a multicolinearidade no qual as variáveis independentes possuem relações lineares exatas ou aproximadamente exatas (correlação alta) entre elas mesmas, indicando que duas ou mais variaveis fornecem a mesma informação sobre a variável resposta. Um índício da existência da multicolinearidade é quando o R^2 é bastante alto (acima de 0,7), mas nenhum dos coeficientes da regressão é estatisticamente significativo segundo a estatística t convencional. A importância de se verificar a existência de multicolinearidade é que podem alterar as estimativas dos parâmetros e fornecer erros-padrão elevados no caso de multicolinearidade moderada ou alta.

Além de verificar a alteração dos parâmetros e seu desvio padrão ao se retirar uma observação, existe uma medida chamada de VIF (fator de inflação da variância) que é utilizada para verificar a partir das correlações o impacto da variância em cada parâmetro. Conforme o VIF aumenta maior o indício de multicolinearidade, entretanto não existem um ponto de corte bem definido, alguns autores recomendam valores acima de 10 como limiar. O cálculo do VIF é dado pela seguinte fórmula

\[VIF_k = (1-R_k^2)^{-1}\]

Banco de dados

O banco de dados utilizado será a base Iris que possui observações acerca de três espécies de plantas e é uma base muito utilizada e conhecida para análises iniciais por ser um banco pequeno, de fácil entendimento e ajuste do modelo.

O objetivo será modelar o comprimento da sépala usando a largura da pétala e sépala, espécie e comprimento da pétala. Depois do ajuste do modelo, será verificado cada pressuposto e se está de acordo com o esperado.

Análise de dados

Para a análise foi utilizado o banco de dados Iris utilizando o ambiente R de computação estatística.

A base de dados pode ser obtida no próprio repositorio do R, é necessário apenas chamar o banco de dados. A descrição das variáveis está disponível no help do R.

Primeiramente, serão lidos os dados e depois ajustado o modelo de regressão linear.

library(car)
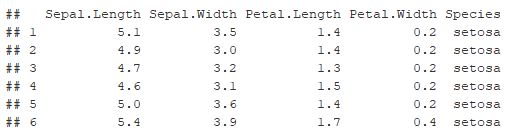
head(iris)
m <- lm(Sepal.Length~., data=iris)

summary(m)

Pelo ajuste do modelo, verificamos que as variáveis são significativas e que o mínimo e máximo dos resídos são inferiores a 1, já sendo um indício que as medidas usando resíduos studentizados devem apresentar valores baixos. Além disso, é necessário verificar a correlação entre as variáveis do modelo.

library(corrplot)
correlacao=cor(iris[,-5])
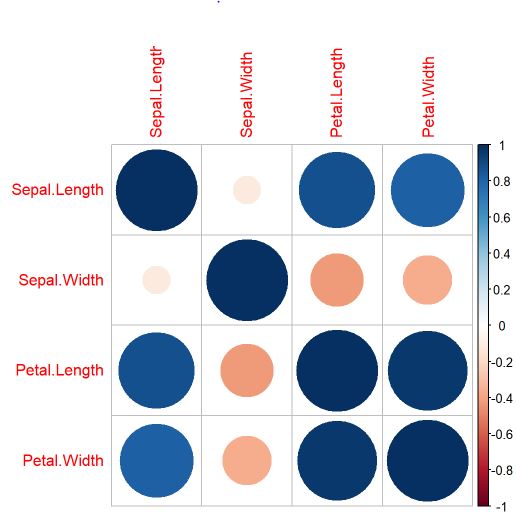
corrplot(correlacao)

Por meio do gráfico de correlação entre as variáveis explicativas é possível verificar que existem algumas variáveis relacionadas e que podem causar multicolineariedade. Essa análise será feita mais adiante.

Primeiramente, será verificado a normalidade dos resíduos studentizados por meio do qqplot e histograma.

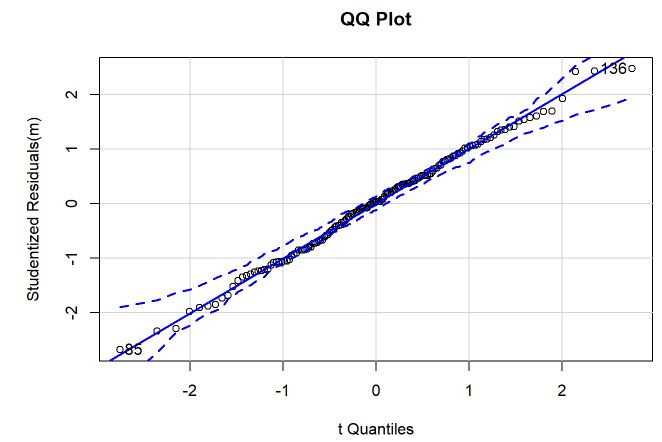
qqPlot(m, main="QQ Plot") #qq plot for studentized resid 

# distribution of studentized residuals
library(MASS)
sresid <- studres(m) 
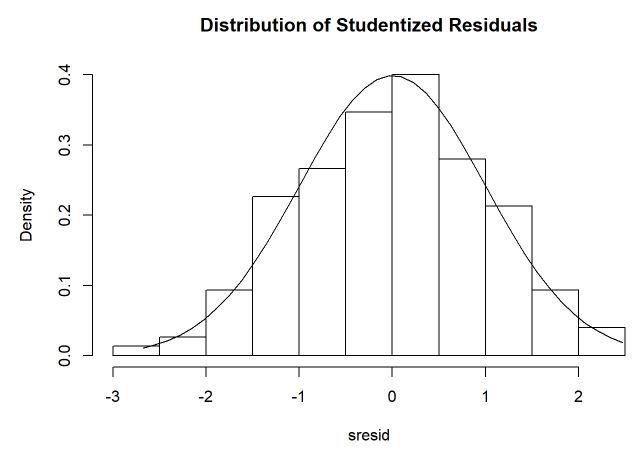
hist(sresid, freq=FALSE, 
     main="Distribution of Studentized Residuals")
xm<-seq(min(sresid),max(sresid),length=40) 
ym<-dnorm(xm) 
lines(xm, ym)

Pelo QQplot, não encontramos indícios de que não existe normalidade nos resíduos porque o comportamento está bem linear e dentro das faixas. As faixas tracejadas são o intervalo de confiança enquanto que o eixo x é o quantil teórico enquanto que o eixo vertical é o empírico. Pelo histograma, é possível ver que os resíduos estão simétricos em torno de 0 e que uma distribuição normal está se ajustando bem aos dados.

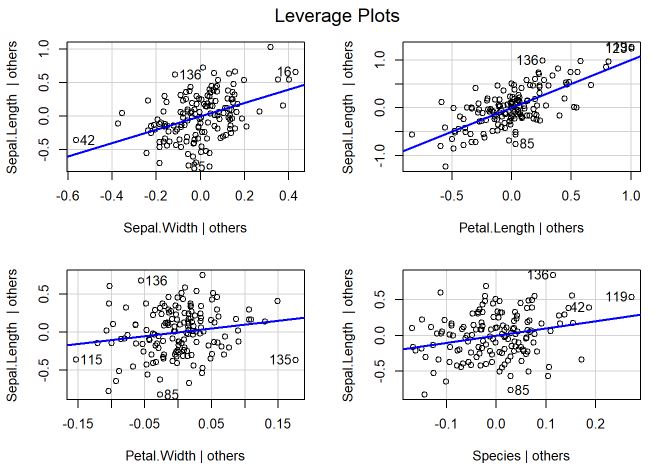
O gráfico do leveragePlots é um gráfico de alavancagem para um efeito fixo que mostra o impacto da adição desse efeito ao modelo, dados os outros efeitos já existentes no modelo. Ou seja, são mostrados os resíduos da regressão usando determinada variável desconsiderando as demais, a reta azul é a regressão e quanto mais distante a observação maior a falta de ajuste.

leveragePlots(m) # leverage plots

Pelos gráficos, é possível analisar que os pontos estão bem próximos da reta e que as distâncias praticamente não ultrapassam 1 nos resíduos, indicando que tem um leverage controlado.

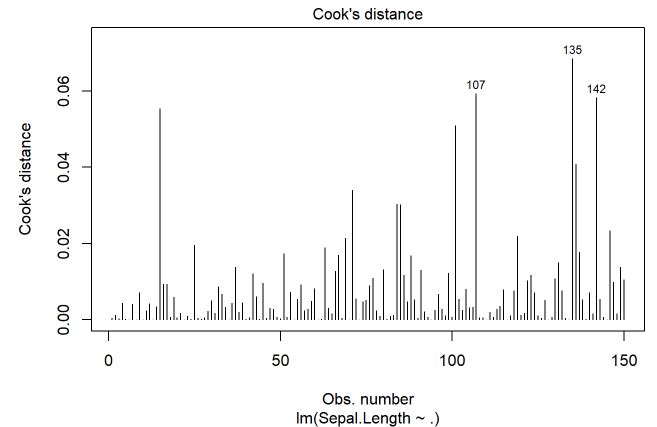
Na sequenência, será feito o gráfico da distância de Cook

# Influential Observations
# Cook's D plot
# identify D values > 4/(n-k-1) 
cutoff <- 4/((nrow(mtcars)-length(m$coefficients)-2)) 
plot(m, which=4, cook.levels=cutoff)

Pelo gráfico não existem indícios de alguma observação (número da observação no eixo horizontal) que esteja acima de 0,50 (considerando uma distância grande), pelo contrário, todas estão abaixo de 0,10.

Dado que não existem valores influêntes, o próximo gráfico verifica os pontos de leverage, outliers e discrepantes conjuntamente.

# Influence Plot 
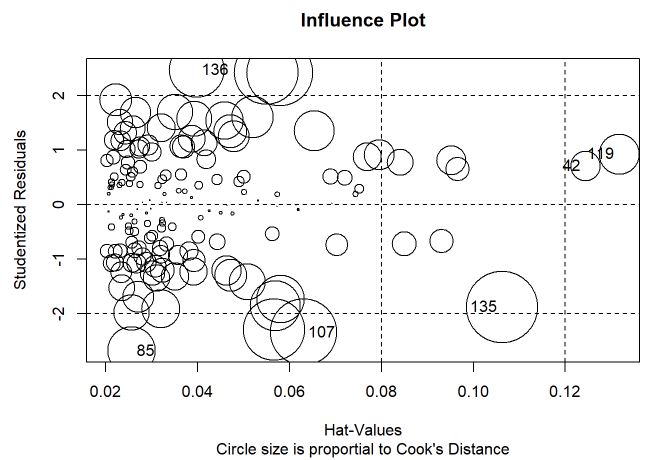
influencePlot(m, id.method="identify", main="Influence Plot", sub="Circle size is proportial to Cook's Distance" )

As linhas acima de 2 e abaixo de -2 indicam os resíduos studentizados mais elevados enquanto que as linhas verticais indicam valores de leverage mais elevados e o tamanho do círculo é proporcional a distância de Cook. Esse gráfico faz a união de diversas medidas e é um ótimo indicativo para quais observações podem se destacar das demais. Nesse estudo, mesmo as observações 42,119 e 135 estarem um pouco afastadas, os valores absolutos de cada medida indicaram que não são observações influentes e que devem atrapalhar de forma geral o ajuste do modelo.

Com relação ao pressuposto da homocedasticidade (variância constante), foi realizado o teste de Breuch-Pagan e NCV que possuem como hipotese nula a homocedasticidade dos resíduos e se baseiam na verossimilhança. Ao realizar os testes, ambos falham em rejeitar a hipotese nula ao nível de 5%, ou seja, não existem indícios de que o pressuposto de homocedasticidade não é respeitado.

# Evaluate homoscedasticity
lmtest::bptest(m)
# non-constant error variance test
ncvTest(m)

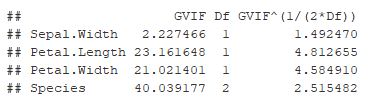
Pela matriz de correlação foi verificado algumas relações entre as variáveis, para verificar o grau de significância disso foi calculado o VIF para cada variável. Pelos resultados, algumas variáveis como comprimento e largura da pétala possuem um valor de VIF que podem influenciar no ajuste, por isso seria interessante refazer o modelo retirando elas e refazer as medidas de diagnóstico para verificar se tem uma alteração brusca nos valores.

# Evaluate Collinearity
vif(m) # variance inflation factors 
vif(m) > 10 # indício

Para verificar independência dos resíduos foi ajustado o teste de Durbin Watson que possui hipótese nula de ausência de correlação serial e sua estatística do teste é construída somente com os resíduos. Ao nível de 5% de significância não encontramos indícios para rejeitar a hipótese de correlação, portanto é mais um pressuposto atendido.

# Test for Autocorrelated Errors
durbinWatsonTest(m)

Para finalizar, a função GVLMA fornece estimativas do ajste do modelo e também verifica automaticamente alguns pressupostos. Ela pode ser útil para uma validação rápida, contudo existem outros pressupostos que são necessários verificar conforme o modelo utilizado.

# Global test of model assumptions
library(gvlma)
gvmodel <- gvlma(m) 
summary(gvmodel)

De forma geral os resultados de diagnóstico foram adequados e apenas a medida do VIF que deveria ser verificada com a retirada de uma variável do modelo.

As técnicas aqui expostas não esgotam o assunto e são apenas algumas das mais utilizadas, existem diversos outros testes e gráficos alternativos para se diagnosticar um modelo. A parte de diagnóstico é imprescindivel para validação de um modelo que possua como objetivo a interpretabilidade e entendimento dos resultados.

Referências

Dobson, Annette J., 1945- An introduction to generalized linear models / Annette J. Dobson and Adrian G. Barnett. – 3rd ed.

Cordeiro, Gauss Moutinho; Demétrio, Clarice Garcia Borges; Moral, Rafael de Andrade. Modelos Lineares Generalizados e Extensões. Piracicaba, setembro de 2016.

Gilberto A. Paula, MODELOS DE REGRESSÃO com apoio computacional.Instituto de Matemática e Estatística Universidade de São Paulo.