Introdução
Tratando-se de problemas de alta complexidade, sobretudo aqueles que envolvem a otimização de certos parâmetros, estão disponíveis diversas metodologias de programação que podem facilitar tanto o entendimento quanto o desenvolvimento da solução. Numa breve revisão, sabe-se que os problemas de otimização possuem geralmente os seguintes aspectos:
- Função objetivo;
- Restrições.
Para exemplificar, vamos supor que trabalhamos em uma empresa de transportes e precisamos levar uma encomenda da cidade D para a cidade C de acordo com o grafo ilustrado na figura 1.

Figura 1: Grafo (obtido em: https://pt.wikipedia.org/wiki/Problema_do_caminho_m%C3%ADnimo)
Os pesos dos arcos representam o custo para ir de uma cidade a outra e queremos gastar o mínimo possível neste trajeto. Logo,
- Função Objetivo: \(min(\sum Custo_{D,C})\).
- Restrições: \(\sum In_i = \sum Out_i\), sendo \(In_i\) as arestas que entram no vértice \(i\) e \(Out_i\) as arestas que saem. Essa restrição, porém, não vale para os vértices de entrada e saída do caminho. Para esses, tem-se que
e
\[In_C = 2, Out_C = 0\]Uma das formas de resolução deste problema seria listarmos todos os caminhos possíveis entre D e C e, ao final, escolhermos a combinação que gerasse o menor custo. Esses são os chamados algoritmos de força bruta. Contudo, note que usá-los poderia tornar o algoritmo computacionalmente dispendioso à medida que o número de vértices e arcos do grafo aumentam. A segunda maneira para encontrar a solução de tal problema seria perceber que para chegarmos em C necessariamente devemos passar por B ou E. Portanto, encontrar a solução ótima partindo da cidade C seria encontrar, antes, a solução ótima da cidade D para a cidade B ou E que são os vértices vizinhos de C. Seguindo o raciocínio, teríamos as possibilidades expressas pela árvore da figura 2.
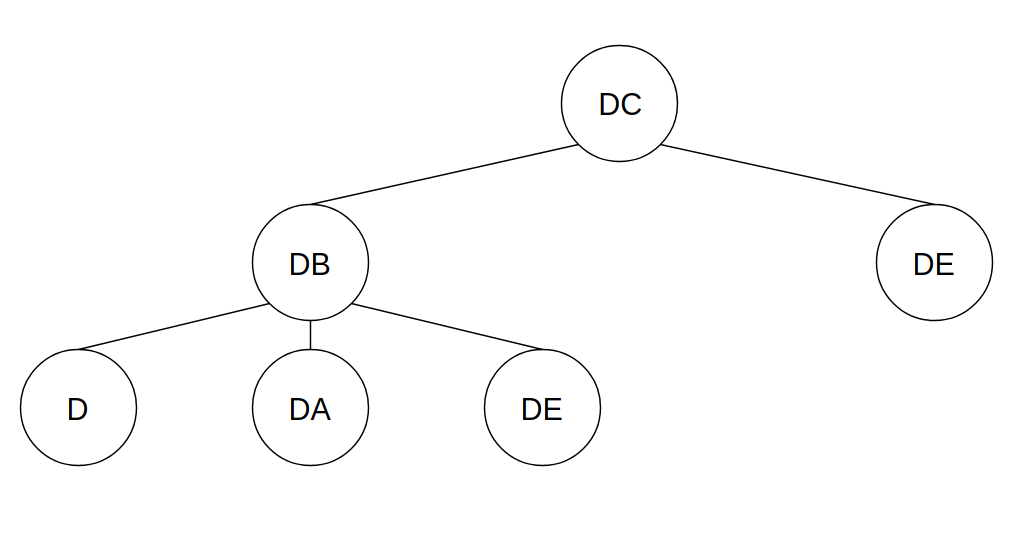
Figura 2: Árvore de possibilidades.
Veja que a solução do caminho ótimo entre a cidade D e E é requisitada por duas vezes caso utilizássemos um algoritmo recursivo. Mas, e se armazenássemos essa solução na memória? Certamente o programa ficaria mais veloz já que estaríamos evitando procedimentos repetidos. Este processo é exatamente o que chamamos de Programação Dinâmica. Dessa forma, a programação dinâmica é um método que busca encontrar a solução de vários subproblemas para, então, encontrar a solução do problema geral. A grande diferença dessa metodologia é que os subresultados são armazenados em memória já que eles são utilizados em diversos momentos dentro do cômputo da solução.
Caracterizando o problema
Nesta seção, vamos utilizar a Sequência de Fibonacci para introduzir alguns aspectos importantes da programação dinâmica. Primeiramente, é sabido que tal série possui o seguinte comportamento:
0, 1, 1, 2, 3, 5, 8, 13,…
em que,
f[n] = f[n - 1] + f[n - 2], para n > 1;
f[0] = 0; f[1] = 1.
A maior dificuldade para usar programação dinâmica não está nas construção dos algoritmos em si, mas em discernir quando ou em que tipo de situação adotar a técnica. Além disso, por muitas vezes a especificação da solução não é trivial. Contudo, de um modo geral, existem quatro passos fundamentais para resolvermos problemas com essa metodologia, a saber:
1 - Identificar o problema como sendo de programação dinâmica
Duas são as características principais para a primeira etapa, a saber:
-
Subestrutura ótima: a solução ótima do problema provém das soluções de subproblemas dependentes. Note que já na especificação do problema vê-se que para poder encontrar o termo n, é necessário encontrar antes o termo n-1 e n-2, ou seja, a solução ótima depende da melhor resultado de outros dois subproblemas. Para fins de conhecimento, o exemplo anterior também apresentava essa estrutura uma vez que, para se chegar em C, era necessário encontrar o caminho de menor custo para E e B e assim sucessivamente.
-
Sobreposição de soluções: a solução ótima passa pela resolução de subproblemas que aparecem duas ou mais vezes. Pela estrutura ilustrada na Figura 3 - tomando como exemplo n = 4 - perceba que o cálculo de fib(2) é requisitado por duas vezes. Assim, encontrar termos dessa série possui sobreposição de soluções.
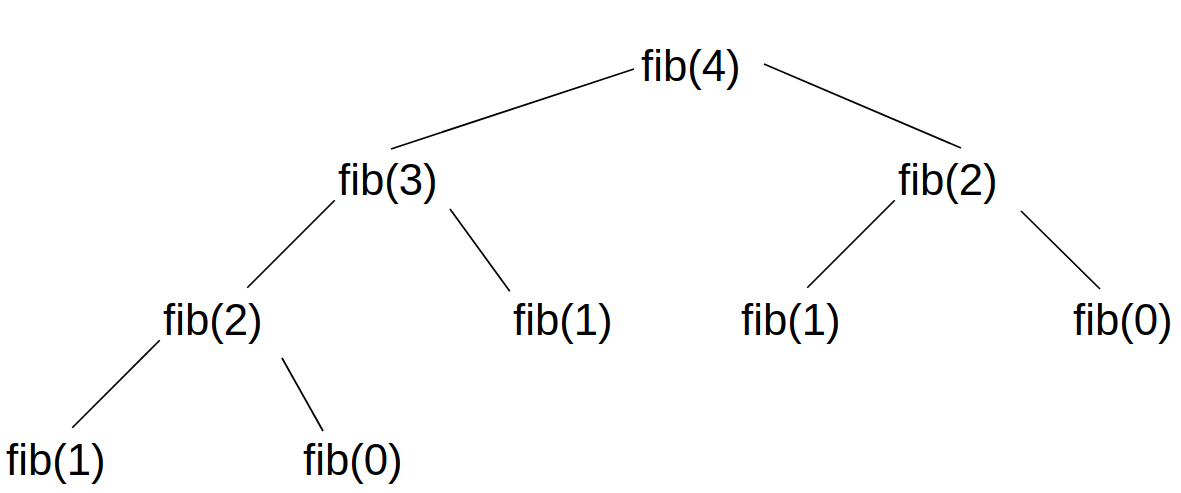
Figura 3: Chamadas recursivas para cálculo de termo da série de Fibonacci.
Entendendo que realmente se trata de um problema cuja solução pode ser encontrada por meio da programação dinâmica, vamos para a segunda etapa.
2 - Definir o valor da solução ótima recursivamente
Para o caso da série de Fibonacci, esta etapa é relativamente simples já que na própria especificação do problema observa-se que a própria função é demandada novamente para descoberta dos termos n-1 e n-2. Levando isso para o python, tem-se:
def fibonacci(n):
if n == 1 or n == 0:
return n
return fibonacci(n-1) + fibonacci(n-2)
3 - Calcular valor da solução ótima da forma “bottom-up” ou “top-down”
Aqui está a diferença no uso de programação dinâmica. Como visto, a ideia da técnica é evitar cálculos repetidos na busca da solução ótima de um problema recursivo. Para isso, cria-se uma estrutura na memória a fim de guardar tais resultados. Há duas abordagens para alcançar tal objetivo as quais serão exploradas a seguir.
Abordagem “Top-Down”
Na abordagem “top-down” (ou memoization, termo inglês), partimos da solução geral ótima que se deseja encontrar e, então, analisa-se quais subproblemas são necessários resolver até que se chegue em um subproblema com resolução trivial. Importante lembrar que ao longo dos cálculos os resultados são armazenados para que sejam reutilizados. Dessa forma, o algoritmo observa primeiramente na tabela se a solução ótima do subproblema já foi computado. Caso positivo, simplesmente extrai o valor. Caso negativo, resolve e salva o resultado na tabela. O código abaixo mostra a solução para a série de Fibonacci usando essa abordagem:
def fibonacciTopDown(n, table = {}):
if n == 1 or n == 0:
return n
try:
return table[n]
except:
table[n] = fibonacciTopDown(n-1) + fibonacciTopDown(n-2)
return table[n]
Abordagem “Bottom-up”
Na abordagem “bottom-up” (ou tabulation, termo inglês), diferente da anterior, a solução ótima começa a ser calculada a partir do subproblema mais trivial. No caso da série de Fibonacci, basta entender que para se calcular o termo n,a resolução sempre inicia pelo fib(0), depois fib(1), fib(2) e assim sucessivamente até chegar em fib(n). O código abaixo mostra a implementação dessa abordagem.
def fibonacciBottomUp(n, table = {}):
table[0] = 0
table[1] = 1
for cont in range(2, n + 1):
table[cont] = table[cont - 1] + table[cont - 2]
return table[n]
Abordagem top-down x bottom-up
Mas afinal, qual a vantagem de se utilizar uma forma ou outra de implementação? A tabela abaixo lista características importantes de cada metodologia.

Figura 4: Top-Down x Bottom-up.
Analisando o Desempenho
Entendidas as características e vantagens de cada abordagem, vamos testar o desempenho de cada uma delas na resolução da série de Fibonacci. Para isso, verificou-se o tempo de execução de cada uma das implementações de acordo com o código a seguir.
import time
for n in range(35, 40):
start = time.time()
result = fibonacci(n)
finish = time.time()
print("===========================================================================")
print("Fibonacci(", n, ")")
print("Resultado - Fibonacci 1 (Original): ", result)
print("Tempo Total de Execução - Fibonacci 1: ", round(finish - start, 2), "segundos")
start = time.time()
result = fibonacciTopDown(n)
finish = time.time()
print("Resultado - Fibonacci 2 (Top-Down): ", result)
print("Tempo Total de Execução - Fibonacci 2: ", round(finish - start, 20), "segundos")
start = time.time()
result = fibonacciBottomUp(n)
finish = time.time()
print("Resultado - Fibonacci 3 (Bottom-Up): ", result)
print("Tempo Total de Execução - Fibonacci 3: ", round(finish - start, 20), "segundos")
print("===========================================================================")
Abaixo encontra-se a saída do código acima.
===========================================================================
Fibonacci( 35 )
Resultado - Fibonacci 1 (Original): 9227465
Tempo Total de Execução - Fibonacci 1: 6.13 segundos
Resultado - Fibonacci 2 (Top-Down): 9227465
Tempo Total de Execução - Fibonacci 2: 3.57627868652344e-06 segundos
Resultado - Fibonacci 3 (Bottom-Up): 9227465
Tempo Total de Execução - Fibonacci 3: 1.740455627441406e-05 segundos
===========================================================================
===========================================================================
Fibonacci( 36 )
Resultado - Fibonacci 1 (Original): 14930352
Tempo Total de Execução - Fibonacci 1: 9.84 segundos
Resultado - Fibonacci 2 (Top-Down): 14930352
Tempo Total de Execução - Fibonacci 2: 3.33786010742188e-06 segundos
Resultado - Fibonacci 3 (Bottom-Up): 14930352
Tempo Total de Execução - Fibonacci 3: 1.454353332519531e-05 segundos
===========================================================================
===========================================================================
Fibonacci( 37 )
Resultado - Fibonacci 1 (Original): 24157817
Tempo Total de Execução - Fibonacci 1: 15.9 segundos
Resultado - Fibonacci 2 (Top-Down): 24157817
Tempo Total de Execução - Fibonacci 2: 5.48362731933594e-06 segundos
Resultado - Fibonacci 3 (Bottom-Up): 24157817
Tempo Total de Execução - Fibonacci 3: 3.743171691894531e-05 segundos
===========================================================================
===========================================================================
Fibonacci( 38 )
Resultado - Fibonacci 1 (Original): 39088169
Tempo Total de Execução - Fibonacci 1: 26.14 segundos
Resultado - Fibonacci 2 (Top-Down): 39088169
Tempo Total de Execução - Fibonacci 2: 3.33786010742188e-06 segundos
Resultado - Fibonacci 3 (Bottom-Up): 39088169
Tempo Total de Execução - Fibonacci 3: 2.574920654296875e-05 segundos
===========================================================================
===========================================================================
Fibonacci( 39 )
Resultado - Fibonacci 1 (Original): 63245986
Tempo Total de Execução - Fibonacci 1: 49.29 segundos
Resultado - Fibonacci 2 (Top-Down): 63245986
Tempo Total de Execução - Fibonacci 2: 7.15255737304688e-06 segundos
Resultado - Fibonacci 3 (Bottom-Up): 63245986
Tempo Total de Execução - Fibonacci 3: 2.717971801757812e-05 segundos
===========================================================================
Escolheu-se o cálculo de termos maiores (35 a 39) para mostrar como o código, usando apenas a recursividade, começa a se tornar extremamente lento à medida que n cresce. Por outro lado, com programação dinâmica, tanto a abordagem top-down quanto bottom-up consegue um desempenho muito superior como pôde ser visto. Além disso, observe também que, nesses casos, a abordagem top-down mostrou-se superior.
Conclusão
Neste post foi apresentada uma introdução sobre programação dinâmica e sua utilidade para a busca de soluções ótimas em problemas de otimização que possuem subestrutura ótima e sobreposição de soluções. Apresentou-se também duas metodologias de implementação da programação dinâmica - abordagem top-down e bottom-up - bem como suas vantagens e desvantagens. Vimos o quão lento a resolução pode se tornar com o uso apenas da recursividade e a grande eficiência alcançada no que tange ao tempo de execução dos códigos provindos do uso de tais metodologias. Caso o leitor se interesse, sugere-se o estudo de questões mais avançadas como:
-
Multiplicação de matrizes encadeadas [1];
-
Problema do Troco [4];
-
Aplicações em Economia para apreçamento de ativos usando Equações de Euler [5].
Referências
-
CORMEN, Thomas H. et al. Introduction to algorithms. MIT press, 2009.
-
Geeks for Geeks: https://www.geeksforgeeks.org/dynamic-programming/#concepts
-
Introduction to Computational Thinking and Data Science (MIT Course): https://www.edx.org/course/introduction-to-computational-thinking-and-data-science-2