Clusterização de texto de reclamação não supervisionada usando K-means com python
fonte: Kreatives Denken steigern mit NLP München
Antes de começarmos, é importante deixar clara a diferença entre classificar um texto e clusterizar um texto. A classificação de texto envolve atrelar categorias já conhecidas aos textos em análise. Já a clusterização envolve agrupar textos em grupos que mais façam sentido, em um número k de grupos. O número k de grupos pode ser conhecido previamente, ou não. Mas como veremos, quando não sabemos o número de k e estamos trabalhando com texto, quase sempre caímos na maldição da dimensionalidade e necessitamos de correção humana para validar o melhor k.
Como nosso objetivo aqui será agrupar textos de reclamação em k categorias, usaremos o recurso de clusterização com k-means.
Os dados e bibliotecas usadas
Os dados usados nessa análise estão em formato .csv e utilizaremos apenas uma coluna chamada “Reclamacao”. Como estamos usando python, nada mais natural que usarmos um DataFrame do Pandas para lidar com nossos dados.
As bibliotecas usadas ao longo de toda a análise são dispostas abaixo:
import pandas as pd
import numpy as np
from sklearn.cluster import MiniBatchKMeans
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import nltk
from sklearn.metrics import silhouette_samples, silhouette_score, v_measure_score
from sklearn.datasets import load_files
import re
from unidecode import unidecode
from mpl_toolkits import mplot3d
Preparando os dados
Antes de iniciarmos o processo de clusterização dos textos, é importante prepararmos os dados adequadamente. Isso nos ajudará a reduzir nossa Matriz Esparsa, eliminando palavras desnecessárias e aglomerando aquelas de mesmo significado. Primeiro, iremos transformar todas as letras do texto para minúsculo. Assim, palavras como “Carro”, “carro” e “CARRO” ficam todas como “carro”.
#converte todas as letras para minúsculo
data["Reclamacao"] = data["Reclamacao"].apply(lambda x: x.lower())
Em seguida removemos quaisquer caracteres que não sejam letras e acentos da língua portuguesa, convertendo as strings para unicode.
#remove números e caracteres especiais
data["Reclamacao"] = data["Reclamacao"].apply(lambda x: re.sub('[0-9]|,|\.|/|$|\(|\)|-|\+|:|•', ' ', x))
#remove acentos
data["Reclamacao"] = data["Reclamacao"].apply(lambda x: unidecode(x))
Por último, aplicamos o método chamado Stemming, o qual reduz as palavras ao seu radical (e.g. enviar, enviado, envio .. viram envi).
#converte as palavras para seu radical
stemmer = nltk.stem.RSLPStemmer()
data["Reclamacao"] = data["Reclamacao"].apply(lambda x: stemmer.stem(x))
Por fim, nossos dados devem estar semelhantes a esse exemplo:

fonte: Chapter 4. Text Vectorization and Transformation Pipelines
Esse tipo de representação de texto é chamado de bolsa de palavras, ou Bag-of-words.
Bag-of-words
Para convertermos o texto analisado em uma linguagem que o computador seja capaz de interpretar, precisamos criar nossa Bag-of-Words. Nessa Bag-of-words, separamos cada palavra em uma coluna, a qual passa a contar o número de aparições daquele termo.
Podemos usar uma frase como exemplo: “The book is on the table” fica:
| The | book | is | on | the | Table |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 |
e “The key is not on the table” fica:
| The | key | is | not | on | the | Table |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Juntando os dois casos temos:
| The | key | book | is | not | on | the | Table |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
Assim, podemos considerar que cada palavra se transforma em uma dimensão representada por um vetor. Esse vetor, embora por um lado tenha eficiência computacional elevada, pode crescer em tamanho muito rapidamente e se tornar um obstáculo. Isso é, porém, facilmente contornado com as configurações adequadas do modelo.
Essa representação geralmente leva em conta alguma forma de significância. Aqui, analisa-se a frequência simples dos termos (apenas para a frase em destaque):

fonte: Chapter 4. Text Vectorization and Transformation Pipelines
Podemos perceber uma fragilidade nessa abordagem, já que algumas palavras como “the” e “can” provavelmente não são tão importantes para compreender o sentido da frase, embora a frequência dela seja a mesma de “echolocation” (para a frase em questão). Esses e outros termos precisam ser considerados, e a simples análise de frequência não é suficiente.
TF-IDF - Importância relativa das palavras.
É importante fazermos uma análise de importância das palavras para identificar aquelas que realmente podem agregar significado à uma sentença. Para isso, é usual empregarmos a técnica da frequência inversa. Com o TF-IDF (term frequency — inverse document frequency), consideramos a frequência de uma palavra na sentença, dividido pelo número de documentos em que ela aparece.

fonte: Can TFIDF be applied to Scene Interpretation?
Assim, uma palavra que aparece muito em uma frase poderia parecer importante, mas se aparecer em 100% dos textos analisados, se tornando uma informação irrelevante.
Alguma palavras, como conectores, podem ter alta correlação com certos assuntos, não representando porém significância, como é o caso das Stopwords. Stopwords são conectores textuais, como “mas”, “porem”, “assim”, os quais podem dificultar nossa análise (já que podem deslocar a média, e nosso modelo é sensível a isso).
Para criarmos nossa bag-of-words, considerando os stopwords, e analisando a frequência inversa dos documentos, usamos os seguintes comandos:
# nltk.download('stopwords')
stopwords = nltk.corpus.stopwords.words('portuguese')
stopwords.extend(["nao"])
vec = TfidfVectorizer(stop_words=stopwords)
vec.fit(data.Reclamacao.values)
features = vec.transform(data.Reclamacao.values)
Assim, um exemplo do resultado final dessa análise seria:

fonte: Chapter 4. Text Vectorization and Transformation Pipelines
Podemos perceber que a palavra “the”, apesar de aparecer na frase em análise, não tem importância para a terceira frase já que aparece em todos os documentos.
O modelo k-means e os desafios da dimensionalidade
O modelo k-means funciona de maneira razoavelmente simples.
Para exemplificar esse funcionamento, usaremos o exemplo da classificação de cães e gatos postado pela computer vision for dummies:
Se tivermos cães e gatos separados em uma dimensão, talvez aconteça de não sermos capazes de perceber nenhuma padrão. Matematicamente (e computacionalmente), isso se traduz em uma dificuldade de se traçar uma reta (ou plano, hiperplano…) que separe os animaizinhos domésticos em questão.

fonte: Computer vision for dummies
Se adicionarmos mais uma dimensão, porém, podemos começar a ter uma visão mais claro do que está acontecendo.

fonte: Computer vision for dummies
Continuando o processo, chegará um momento no qual atingiremos o estado ótimo (significando apenas que não há melhoria possível) e teremos algo como o abaixo:

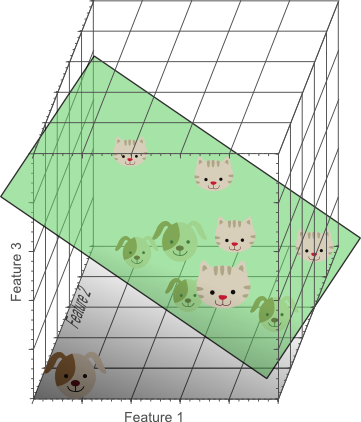
fonte: Computer vision for dummies
Analisamos os resultados para 1, 2 e 3 dimensões para separar os gatinhos dos cachorros. E se continuarmos acrescentando dimensões? Nosso resultado continuará melhorando? A resposta curta é não, devido a dimensionalidade. Mas voltaremos nesse assunto (e pets) mais abaixo.
Assim, utilizando-se as dimensões geradas na vetorização das sentenças (lembrando que cada palavra é uma dimensão) e sua relativa frequência (TFIDF), tenta-se separar os clusters maximizando as distâncias entre a média da distância dos pontos (reclamações, no caso). Matematicamente, essa expressão fica:
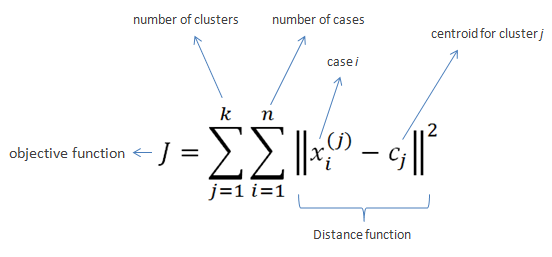
Como não sabemos o número de clusters que iremos usar, iremos testar algumas opções. Aqui, começaremos a testar k variando entre 2 e 29. Para começar criamos um loop que roda uma vez para cada opção, classificando todos os textos em clusters: 1, 2, …:
for cluster in range(2,30):
cls = MiniBatchKMeans(n_clusters=cluster, random_state=random_state)
cls.fit(features)
# predict cluster labels for new dataset
cls.predict(features)
# to get cluster labels for the dataset used while
# training the model (used for models that does not
# support prediction on new dataset).
cls.labels_
Em seguida, analisamos uma métrica estatística que avalia a distância de cada grupo. Em regra, quanto maior a distância entre os grupos, melhor é o resultado. Para isso, usamos o indicador Silhouete. O valor -1 significa classificação totalmente imperfeita, 1 totalmente perfeita, e valores no meio representam sobreposições.
O código para isso fica:
silhouette_avg = v_measure_score(X, cluster_labels)
print("For n_clusters =", w,
"The average silhouette_score is :", silhouette_avg)
E o resultado para os primeiros clusters:
Para número de clusters = 2 o valor médio do silhouette_score foi : 0.02266700210191528
Para número de clusters = 3 o valor médio do silhouette_score foi : 0.005991902728057088
Para número de clusters = 4 o valor médio do silhouette_score foi : 0.005276593705042646
Para número de clusters = 5 o valor médio do silhouette_score foi : 0.005690178439257757
Para número de clusters = 6 o valor médio do silhouette_score foi : 0.004483731771877256
Para número de clusters = 7 o valor médio do silhouette_score foi : 0.004786106699286532
Para número de clusters = 8 o valor médio do silhouette_score foi : 0.005219537391930194
Para número de clusters = 9 o valor médio do silhouette_score foi : 0.005530513106476973
Para número de clusters = 10 o valor médio do silhouette_score foi : 0.005672599203188975
Os valores, como observados, estão longe do ideal (1). Isso, porém, se deve a maldição da dimensionalidade, que implica que se utilizarmos dimensões além do necessário, estaremos causando overfitting em nossos dados, criando um caso artificialmente positivo, capaz apenas de funcionar para o cenário de treinamento.
Além disso, podemos citar a dificuldade inerente desse processo, já que as variáveis (então tratadas como independentes) são influenciadas por muitas outras variáveis, mas nenhuma em especial.
Como referencial dos nossos dados, eles já contam com duas labels que os dividem em 12 grupos e 120 subgrupos. Isso poderia nos indicar que existe uma divisão lógica nesses pontos. Analisamos, então, os clusters até 150.
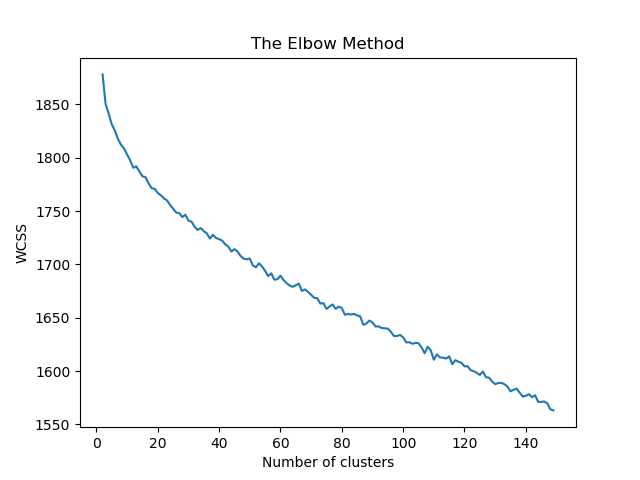
Uma forma de se julgar esses números, é analisar a técnica do cotovelo. Nela, procura-se o número de clusters que faz com que o ganho se torne marginal. Como nossa curva se aproxima de uma reta, não é possível visualmente escolher qualquer número de clusters (para o nossa caso, tratando de textos).
Dessa forma, considerando que processamentos de texto lidam com milhares de dimensões em uma mesma análise, já era esperado que os resultados sofressem dessa maldição.
Isso, porém, não significa que os clusters não sejam relevantes ou tenham qualquer prejuízo interpretativo. Na prática, a maldição da dimensionalidade implica apenas que é necessário input humano para decidir o melhor número de clusters.
Resultados gráficos
Embora os resultados anteriores já sejam suficientes para compreendermos o que está acontecendo, podemos plotar os resultados em duas e três dimensões para podermos visualizar o que está acontecendo. Precisamos, então, plotar os pontos individuais (cada reclamação), de acordo com a cor de cada grupo, e identificarmos o centro desses grupos numericamente.
Para isso precisamos, antes de mais nada, converter nossas informações de cluster para 2 e 3 dimensões para sermos capazes de visualizar esses dados:
fig = plt.figure(figsize=plt.figaspect(0.5))
ax = fig.add_subplot(1, 2, 1)
#Visualização gráfica 2D
# Converte as features para 2D
pca = PCA(n_components=2, random_state= 0)
reduced_features = pca.fit_transform(features.toarray())
# Converte os centros dos clusters para 2D
reduced_cluster_centers = pca.transform(cls.cluster_centers_)
#Plota gráfico 2D
ax.scatter(reduced_features[:,0], reduced_features[:,1], c=cls.predict(features))
ax.scatter(reduced_cluster_centers[:, 0], reduced_cluster_centers[:,1], marker='o', s=150, edgecolor='k')
#Plota números nos clusters
for i, c in enumerate(reduced_cluster_centers):
ax.scatter(c[0], c[1], marker='$%d$' % i, alpha=1,
s=50, edgecolor='k')
#Adiciona informações no gráfico
plt.title("Análise de cluster k = %d" % cluster)
plt.xlabel('Dispersão em X')
plt.ylabel('Dispersão em Y')
#Visualização gráfica 3D
ax = fig.add_subplot(1, 2, 2,projection="3d")
# ax = plt.axes(projection="3d")
# Adiciona informações no gráfico
plt.title("Análise de cluster k = %d" % cluster)
plt.xlabel('Dispersão em X')
plt.ylabel('Dispersão em Y')
#converte dados para 3D
pca = PCA(n_components=3, random_state=0)
reduced_features = pca.fit_transform(features.toarray())
#Plota dados em 3D
ax.scatter3D(reduced_features[:,0], reduced_features[:,1], reduced_features[:,2], marker='o', s=150, edgecolor='k', c=cls.predict(features))
# Converte os centros dos clusters para 3D
reduced_cluster_centers = pca.transform(cls.cluster_centers_)
#Salva arquivo de imagem 3D
plt.savefig("imagens/grafico_cluster_k=%d" % cluster)
plt.show()
E os resultados para os primeiros cluster podem ser vistos abaixo:
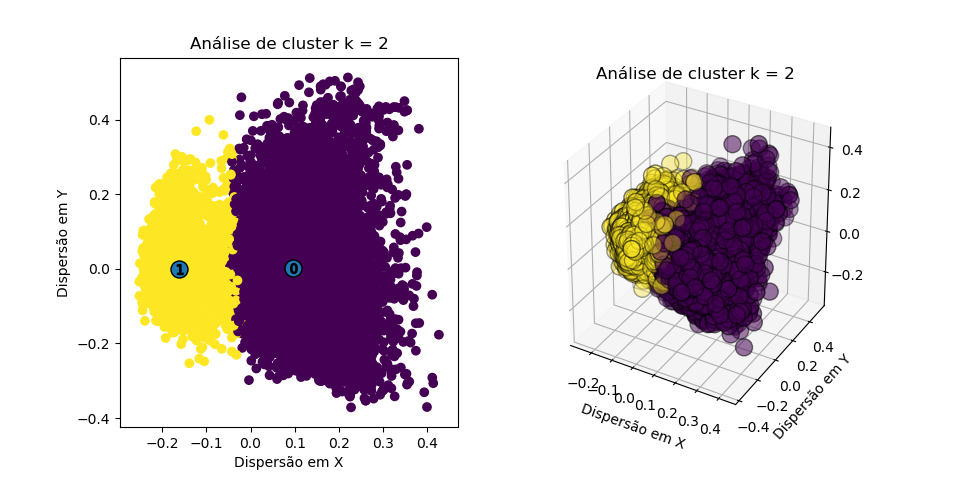
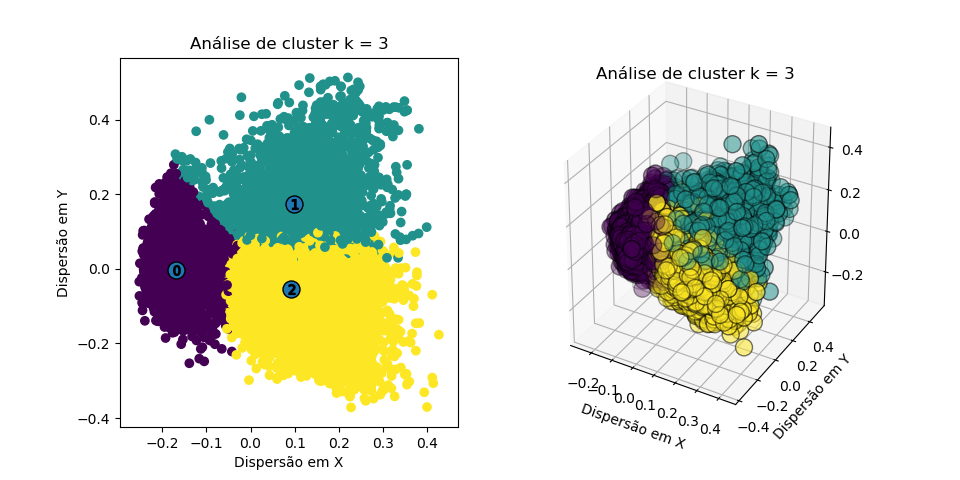
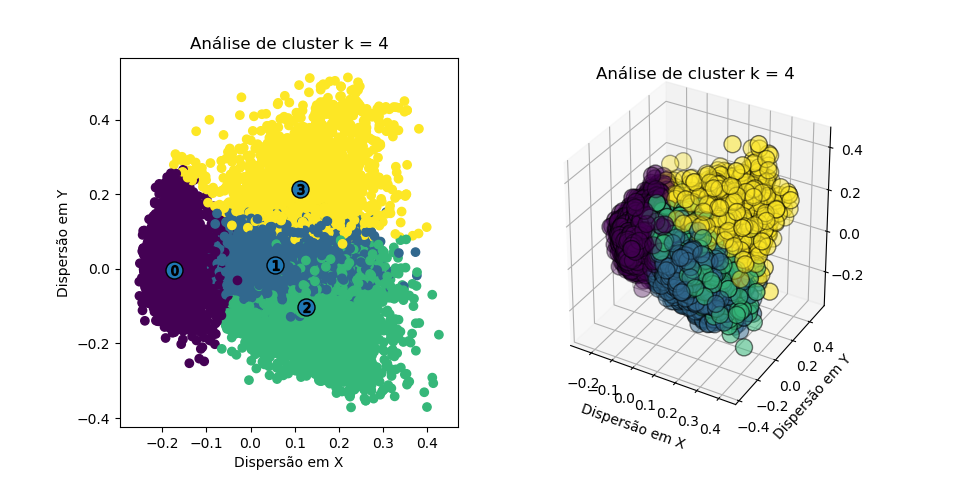
Podemos perceber, então, que os clusters se formam de maneira clara, com fronteira razoavelmente bem definida. Contudo, devido a dimensionalidade, não podemos definir qual número de clusters faz mais sentido apenas pelos resultados (as fronteiras estão se sobrepondo).
Precisamos, então, de uma verificação humana.
Validando os resultados
Com os resultados acima identificados, podemos perceber que o silhouete não pode nos dar pistas sobre o melhor número de clusters, mas isso não tem relação alguma com a qualidade dos grupos que estão sendo formados, como mostram os gráficos de clusters. Resta, assim, que seja feita uma validação humana para decidir quais clusters fazem mais sentidos, dependendo da intenção que exista com essa classificação.
O código a seguir exporta as palavras mais importantes de cada cluster, para cada opção de número de cluster.
writer = pd.ExcelWriter('Output/resultados_classificacao.xlsx', engine='xlsxwriter')
#Estrutura os dados em uma lista por cluster para exportar ao excel
resultado = list()
header = list()
for i in range(true_k):
header.append("Cluster " + str(i)) # Nome das colunas
principais_palavras_cluster = [terms[x] for x in order_centroids[i, : 21]] # listas com palavras ordenadas
resultado.append(principais_palavras_cluster) # exporta resultados para uma lista de listas
#Junta os resultados em um DataFrame
resultados = pd.DataFrame(resultado, index = header)
resultados = resultados.T
# print(resultados)
#salva cada analise em uma aba do excel
resultados.to_excel(writer, sheet_name= "K = " + str(true_k))
wcss.append(model.inertia_)
# Salva os resultados no Excel
writer.save()
A primeira aba da planilha deverá se parecer com a seguir:
| Cluster 1 | Cluster 2 |
|---|---|
| Palavra 1 | Palavra 1 |
| Palavra 2 | Palavra 2 |
| … | … |
| Palavra n | Palavra n |
Com essas informações em mãos, é possível usar input humano para decidir as categorias que mais fazem sentido, para em seguida etiquetar automaticamente cada reclamação como sendo pertencente de um grupo, ou outro.
Após decidirmos o número k de clusters, podemos definir a seguinte função:
def categoriza(input):
X = vec.transform(input)
predicted = cls.predict(X)
return predicted
Input:
clusteriza(["qual o grupo dessa frase?"])
Output:
cluster = [1]
Conclusão
Com o uso da planilha gerada no passo anterior, podemos coletar input humano que nos auxilie a definir o k que mais gere valor para nossa análise. Embora o uso de k-means seja uma técnica considerada não-supervisionada, o uso com NLP nos força a usar de recursos que exigem uma forma de supervisionamento.
Treinamos a máquina a aprender os critérios que fariam mais sentido servirem como separador dos grupos, preparamos os dados para análise, convertemos esses dados em uma linguagem que o computador possa interpretar, e criamos um classificador que recebe qualquer texto e o classifica como pertencendo a algum dos grupos.