Análise Discriminante Linear

1. Introdução

A Análise Discriminante Linear (em sua sigla em inglês, LDA) é uma ferramenta usada para classificação, redução de dimensão e visualização de dados. A meta em se aplicar técnicas de redução de dimensões é remover aquelas características redundantes e dependentes ao transformar características de um espaço dimensional maior para um espaço dimensional menor.

O método foi introduzido em sua forma inicial para problemas com duas classes por Robert Fisher em 1936, mas é particularmente útil com amostras de dados multivariados. Tem aplicações em diversos campos do conhecimento, como na biologia (para classificações taxonômicas), nas finanças (o Z-score de Altman para previsão de falências) e na tecnologia (para reconhecimento de dígitos), entre outros.

2. Classificação por análise de discriminante

Temos o seguinte problema: uma variável aleatória $\mathbf{X}$ pode ser incluída em uma de $\mathbf{J}$ classes, com densidade de probabilidade $f_{j}(\mathbf{x})$. A regra discriminatória tenta dividir o espaço de dados em $\mathbf{J}$ regiões que representam as classes. A análise de discriminante tem como objetivo alocar $\mathbf{x}$ à classe $j$ se $\mathbf{x}$ está na região de $j$.

Podemos seguir duas regras de alocação:

1. Regra de máxima verossimilhança: a hipótese é de que cada classe pode ocorrer com a mesma probabilidade. Então alocamos $\mathbf{x}$ para $j$ se $j = arg\, max_i\,f_i(\mathbf{x})$
2. Regra Bayesiana: nesse caso, já temos as probabilidades de ocorrência $\pi_1,…,\pi_{\mathbf{J}}$ de cada classe; alocamos $\mathbf{x}$ a cada classe $j$ se $j = arg\,max\,\pi_{i}f_{i}(\mathbf{x})$

2.1 Análise discriminante linear vs. quadrática

Assumindo que os dados seguem uma distribuição Gaussiana multivariada, em que $\mathbf{X} \thicksim N(\mu, \Sigma)$, podemos obter funções de alocação. Seguindo a regra Bayesiana, classificamos $\mathbf{x}$ na classe $j$ se $j = arg\,max\,\delta_i(\mathbf{x})$ onde a função discriminatória $\delta_i(\mathbf{x})$ é dada por

O LDA aparece no caso em que assumimos igual covariância entre as $\mathbf{J}$ classes – isso implica que assumimos igual grau de interdependência numérica entre as classes; a fronteira de decisão entre os pares de classes será uma função linear em $\mathbf{x}$. Assim, podemos obter a seguinte função discriminatória, usando a função de verossimilhança com distribuição Gaussiana:

Sem a hipótese de mesma covariância entre as classes, a função discriminante resultante é uma função quadrática em $\mathbf{x}$, conhecida como análise discriminante quadrática (QDA):

Comparando ambas as análises podemos observar que, enquanto o QDA acomodaria fronteiras de decisão mais flexíveis em relação ao LDA, a quantidade de parâmetros a serem estimados na análise quadrática cresce a um ritmo mais rápido, com impactos sobre o desempenho da análise.

Outras extensões do LDA incluem a Análise Discriminatória Flexível (FDA), onde combinações não-lineares dos inputs são usadas, e a Análise Discriminatória Regularizada (RDA), que introduz regularização à estimação da covariância.

2.2 Computação para LDA

Podemos transformar os dados para deixá-los mais próximos a uma distirbuição Gaussiana, e padronizá-los para que apresentem média zero e desvio padrão unitário, de forma a facilitar a análise.

Além disso, podemos simplificar a computação de funções discriminatórias se diagonalizarmos as matrizes de covariância. O que faremos é transformar os dados de modo a obter uma matriz identidade de covariância (sem correlação e com variância unitária).

1. Aplicamos auto-decomposição na matriz de covariância: $\mathbf{\hat{\Sigma} = UDU^{T}}$
2. Esferizamos os dados: $\mathbf{X^{*} \rightarrow D^{-\tfrac{1}{2}}U^{T}X}$
3. Obtemos as médias das classes no espaço transformado: $\hat{\mu}_1,…,\hat{\mu}_J$
4. Classificamos $\mathbf{x}$ segundo $\delta_j(\mathbf{x^{*}})$:

Vamos ver o princípio de alocação do LDA em termos matemáticos. Suponha que existam duas classes, $k$ e $l$, e queremos classificar os dados $\mathbf{x}$. Classificaremos em $k$ se:

Onde

\begin{split} \delta_k(\mathbf{x^{}}) - \delta_l(\mathbf{x^{}}) &= \mathbf{x^{}}^{T}\hat{\mu}_k-(1/2)\,\hat{\mu}_k^{T}\hat{\mu}_k + log\,\hat{\pi}_k - \mathbf{x^{}}^{T}\hat{\mu}_l-(1/2)\,\hat{\mu}_l^{T}\hat{\mu}_l + log\,\hat{\pi}_l
&= \mathbf{x^{*}}^{T}\,(\hat{\mu}_k-\hat{\mu}_l) -(1/2)\,(\hat{\mu}_k^{T}\hat{\mu}_k-\hat{\mu}_l^{T}\hat{\mu}_l) + log\,\hat{\pi}_k/\hat{\pi}_l
&> 0 \end{split}

Isto é, classificamos $\mathbf{x}$ em $k$ se:

Na equação à esquerda, temos o comprimento da projeção ortogonal de $\mathbf{x}^{*}$ na linha de segmento que une as médias das classes. No lado direito, temos a locação do centro do segmento corrigida pelas probabilidades das classes.

Essencialmente, o LDA compara distâncias entre as médias dos dados e as médias das classes, e os classifica junto àquela que apresenta a média mais próxima.

3. Redução de dimensão com LDA

A redução de dimensionalidade tem como objetivo facilitar a visualização e tratamento de dados com várias dimensões. Essa redução é inerente à técnica do LDA. Comparando a distância no subespaço dado pelas $J$ médias das classes, nota-se que distâncias ortogonais a esse subespaço não adicionam novas informações pois contribuem de igual forma para cada classe. Assim, podemos transformar um problema $p$-dimensional para um problema com $J-1$ dimensões ao projetar os dados ortogonalmente nesse subespaço.

Podemos ir além, e construir um subespaço $L$-dimensional $H_L$ (onde $L < J$). Esse subespaço é ótimo quando as médias das classes dos dados esfericizados têm máxima separação em termos de variância. As coordenadas do subespaço ótimo são encontradas aplicando um Principal Component Analysis (PCA) nas médias das classes esfericizadas, porque o PCA encontra a direção da variância máxima.

1. Encontramos a matriz das médias das classes, $\mathbf{M}{(J \times p)}$, e variância-covariância agrupada, $\mathbf{W}{(p \times p)}$

1. Esferizamos as médias, usando uma auto-decomposição de $\mathbf{W}$: $\mathbf{M^{*}} = \mathbf{MW}^{-1/2}$

2. Computamos $\mathbf{B^{}} = cov(\mathbf{M}^{})$, a covariância entre classes das médias esfericizadas das classes:

1. PCA: obtemos $L$ autovetores $\mathbf{v}_l^{*}$, correspondendo aos $L$ maiores autovalores, que definem as coordenadas do subespaço ótimo

2. Obtemos as novas $L$ variáveis discriminantes $Z_l - (\mathbf{W}^{-1/2}\,\mathbf{v}_l^{*})^{T}\,X$, para $l = 1,…,L$

Através desse procedimento, reduzimos nossos dados de $\mathbf{X}{(n \times p)}$ para $\mathbf{Z}{(n \times L)}$, reduzindo a dimensão do problema de $p$ para $L$.

O LDA cria um novo eixo e projeta os dados ortogonalmente de forma a minimizar a variância e maximizar a distância entre as médias das classes. No exemplo acima, a simples projeção ortogonal no eixo horizontal não é ótima pois as informações atreladas à separação dos dados em classes foi perdida. No segundo caso, com a aplicação de um LDA, corrige-se esse problema.

O que se espera com a aplicação de um LDA é que a variância entre classes seja maximizada relativamente à variância intra-classe.

4. Exemplo

Pode-se separar elementos de uma amostra em subgrupos no R utilizando o pacote MASS, como veremos no exemplo abaixo.

4.1 Carregar Pacotes necessários

#o primeiro passo é instalar e chamar as bibliotecas necessárias

#esse pacote contém a base de dados utilizada
install.packages("ISLR")
library("ISLR")

#esse pacote contém a função lda

install.packages("MASS")
library("MASS")

4.2 Preparar a base de dados

Nesse exemplo, utilizaremos a base de dados Smarket, que apresenta os retornos percentuais diários para o índice de ações S&P 500 entre 2001 e 2005, para prever a direção do retorno do mercado.

$Direction$ ~ Um fator com níveis Down e Up que indica se o mercado teve um retorno positivo ou negativo em um determinado dia

As variáveis preditoras utilizadas são:

$Year$ ~ O ano em que a observação foi registrada

$Lag_i$ ~ Retorno percentual de i dias anteriores

$Volume$ ~ Volume de ações negociadas (número de ações diárias negociadas em bilhões)

$Today$ ~ Retorno percentual para hoje

#chamando a base de dados Smarket
data("Smarket")
?Smarket
#essa função permite chamar as colunas pelo seus respectivos nomes sem a necessidade de informar a base de dados
attach(Smarket)

Após chamar os dados, serão feitos breves análises e tratamentos da base de dados antes de realisar a análise discriminante.

# primeiro passo, dividir a base de dados em train e test
## note que não foi necessário colocar ISLR$Smarket, pois a função attach() simplificou o processo
Smarket_train <- Smarket[1:1000,]
Smarket_test <- Smarket[1001:1250,]

O algoritmo LDA começa encontrando direções que maximizam a separação entre as classes e, em seguida, usa essas direções para prever a classe de indivíduos. Essas direções, chamadas discriminantes lineares, são combinações lineares de variáveis preditoras.

4.3 Modelo

Abaixo será usada a regressão lda para explicar a variável $Direction$.

#Direction é uma dummy que pode ser up ou down
modelo_analise <- lda(Direction~Lag1+Lag2+Lag3+Lag4+Lag5+
                        Volume+Today, data=Smarket_train)
#ao plotar, vemos que tem uma interceção muito pequena o que é bom
modelo_analise

Call:
lda(Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume + Today,
    data = Smarket_train)

Prior probabilities of groups:
 Down    Up
0.493 0.507

Group means:
            Lag1        Lag2         Lag3         Lag4          Lag5   Volume      Today
Down  0.04069777  0.03350101 -0.009764706 -0.009119675  0.0049249493 1.370938 -0.9232049
Up   -0.03954635 -0.03132544  0.005834320  0.003110454 -0.0006508876 1.363210  0.8946864

Coefficients of linear discriminants:
               LD1
Lag1   -0.02753403
Lag2   -0.03289355
Lag3    0.01128884
Lag4    0.01327753
Lag5    0.04349531
Volume -0.12206753
Today   1.20995907

plot(modelo_analise)

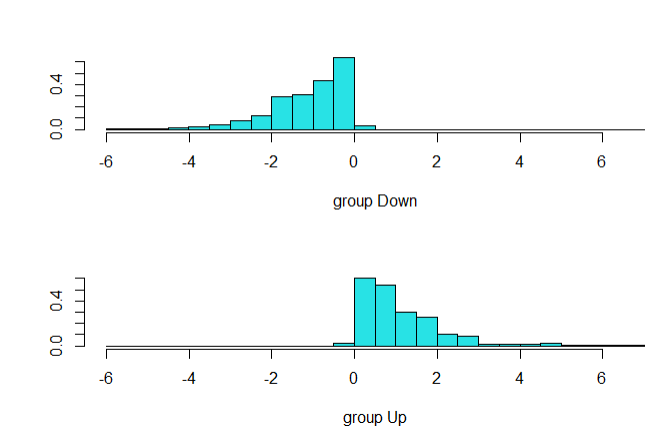
modelo_analise$means

            Lag1        Lag2         Lag3         Lag4          Lag5   Volume      Today
Down  0.04069777  0.03350101 -0.009764706 -0.009119675  0.0049249493 1.370938 -0.9232049
Up   -0.03954635 -0.03132544  0.005834320  0.003110454 -0.0006508876 1.363210  0.8946864

O LDA determina as médias dos grupos e calcula, para cada indivíduo, a probabilidade de pertencer aos diferentes grupos. O indivíduo é então afetado ao grupo com a pontuação de probabilidade mais alta.

Coeficientes de discriminantes lineares : Mostra a combinação linear de variáveis preditoras que são usadas para formar a regra de decisão LDA.

Ao plotar o gráfico, pode-se observar que há uma pequena interseção entre os dados, o que representa que o modelo aparenta possuir uma boa acurácia, que será calculada posteriomente.

4.4 Previsões

Após utilizar o algoritmo de discriminante linear, pode-se usar o modelo para prever a probabilidade de uma observação x pertencer ao grupo $Down$ ou ao grupo $Up$.

A função $predict()$ retorna os seguintes elementos:

$class$ ~ classes previstas de observações.

$posterior$ ~ é uma matriz cujas colunas são os grupos, as linhas são os indivíduos e os valores são a probabilidade posterior de que a observação correspondente pertença aos grupos.

$x$ ~ contém os discriminantes lineares, descritos acima

#utilizar a função predict para prever  o modelo
modelo_predict <- predict(modelo_analise, Smarket_test[,-9])
names(modelo_predict)

[1] "class"     "posterior" "x"

#após prever o modelo, utiliza-se a função table para comparar os valores previstos com o valor da amostra de teste
lda.class <- modelo_predict$class
#table apresenta os acertos do modelo
table(lda.class, Smarket_test$Direction)

lda.class Down  Up
     Down  108   7
     Up     1   134

4.5 Acurácia do modelo

Por fim, as funções predict e table foram utilizadas para prever os valores do modelo e comparar com a amostra Smarket_test. Note que o resultado confimou a observação feita pelo gráfico.

#Cálculo da acurácia de 96,8%
1-(1+7)/(1+7+108+134)

[1] 0.968

Há 250 observações nos dados $Smarket_test$. Na matriz lda.class, observa-se que o modelo previu que 1 observação era Up, quando na realidade era Down, e outras 7 eram Down, quando na realidade deveria ser Up. De acordo com o gráfico, há uma interseção pequena entre os dados discriminados, o que foi confirmado pela acurácia de 96,8%.

5. Conclusão

As principais vantagens do LDA são relacionadas à sua simplicidade como método de classificação, com limites de decisão lineares robustos e propriedades de redução de dimensão, que produzem uma ferramenta de fácil interpretação, visualização e modelagem.

As principais desvantagens também estão ligadas a essa relativa simplicidade do método, na medida em que a linearidade pode não ser adequada para determinados tipos de classificação e modelagem, o que implicaria na necessidade de adoção de análises mais complexas como forma de complementação.

Referências

Linear and Quadratic Discriminant Analysis. Scikit Learn. Disponível em: https://scikit-learn.org/stable/modules/lda_qda.html

BROWNLEE, Jason. Linear Discriminant Analysis for Machine Learning. Machine Learning Mastery, 2016. Disponível em: https://machinelearningmastery.com/linear-discriminant-analysis-for- machine-learning/

SAWLA, Srishti. Linear Discriminant Analysis. Medium Data Sciene, 2018. Disponpivel em: https://medium.com/@srishtisawla/linear-discriminant-analysis-d38decf48105

SCHLAGENHAUF, Tobias. Linear Discriminant Analysis (LDA). Python Machine Learning Tutorial. Disponível em: https://www.python-course.eu/linear_discriminant_analysis.php

XIAOZHOU, Yang. Linear Discriminant Analysys, Explained. Xiaozhou’s Notes, 2019. Disponível em: https://yangxiaozhou.github.io/data/2019/10/02/linear-discriminant-analysis.html

• ← Previous Post
• Next Post →