Aprendizado Semi-Supervisionado para Detecção de Fraudes [Parte 3]

Esta é a continuação (final) da série de postagens sobre detecção de fraudes, post1, post2. Nesta última etapa apresentaremos mais algumas técnicas semi-supervisionadas para detecção de anomalia e uma breve conclusão. Vamos lá!

Modelo de Máquina de Suporte Vetorial

Máquinas de Suporte Vetoriais (MSV) são uma classe de modelos originalmente desenhadas para problemas supervisionados de categorização (ou classificação), em que o objetivo é separar dois tipos de observação. Intuitivamente, o que os MSVs fazem é achar o melhor plano de separação entre os dois tipos de dados. Isso pode parecer um pouco restritivo, já quem muitas vezes a superfície que separa duas classes de dados é composta por várias curvaturas, algo que um plano não conseguiria representar. Para superar essa limitação, as MSV fazer uso do truque do kernel, que representa os dados originais em um espaço dimensional maior, de forma que seja possível separar os dois tipos nesse novo espaço.

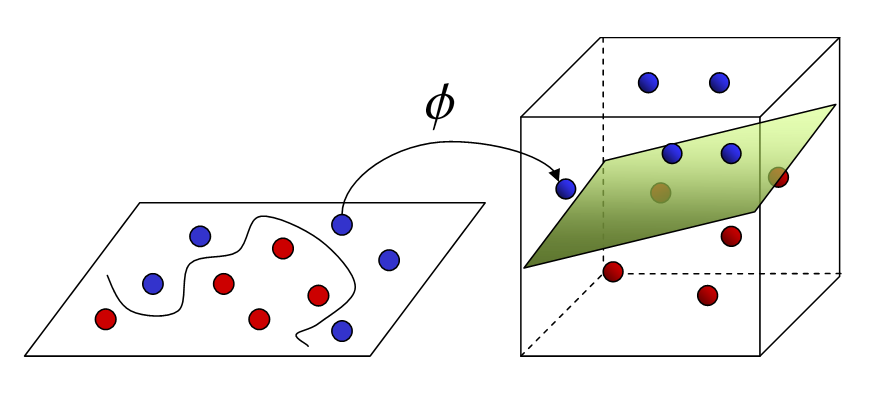
Na imagem acima, vemos como o truque do kernel representa dados em altas dimensões de forma que eles possam ser separados por um plano. As MSVs não são os únicos modelos que podem se beneficiar do truque do kernel, mas elas são especialmente otimizadas por ele. Na verdade, o truque do kernel é tão computacionalmente ineficiente que se torna praticamente proibitivo de ser utilizado com qualquer técnica que não as máquinas de suporte vetorial.

Na versão não supervisionada da MSV, não estamos interessados em separar dois tipos de dados, pois os dados sequer são nomeados com os tipos. Em vez disso, queremos achar a melhor esfera que encapsule todos os dados. É fácil ver como isso é útil no problema de detecção de anomalias: a esfera que contiver os dados normais será definida como nossa fronteira de normalidade, de forma que dados fora dela serão classificados como anomalias. Mas e se os dados normais não se agruparem em uma esfera, mas em uma forma mais complicada? Como talvez, duas esferas ou um ovo? Isso também não é um problema para a versão não supervisionada das MSV, pois podemos usar o truque do kernel e representar os dados em uma dimensão maior até que eles estejam contidos em uma esfera

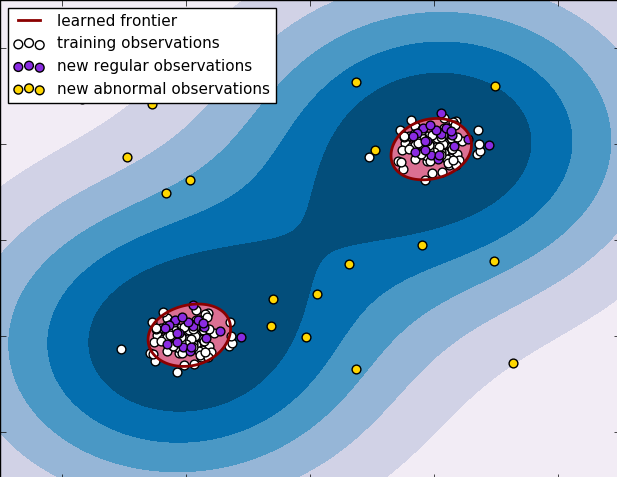
Na imagem abaixo, por exemplo, a região de normalidade é compreendida por duas esferas disjuntas, mas podemos ver como uma MSV consegue representar bem essas fronteiras. Na verdade, nós podemos dizer que o modelo não supervisionado de MSV é um aproximador universal de funções densidade de probabilidade, isto é, ele é capaz de aproximar qualquer distribuição possível. Uma severa desvantagem desse método é o fato dele ser extremamente ineficiente para treinar. Apenas para se ter uma ideia, dos modelos aqui avaliados, o segundo mais demorado de treinar é o de mistura de gaussianas, que leva aproximadamente 5min. O modelo MSV, por sua vez leva em torno de uma hora.

Após treinado, o modelo produz uma superfície de separação e nós podemos usar a distância entre uma observação e essa superfície como uma pontuação de anomalia para a observação. Distâncias negativas significam que a observação está fora da esfera definida pela superfície. Assim, quanto mais negativa a pontuação, maior a probabilidade da amostra ser uma anomalia. Usando a subamostra de validação, nomeada com tipos normais e anômalos, nós ajustamos um limiar para essa pontuação.

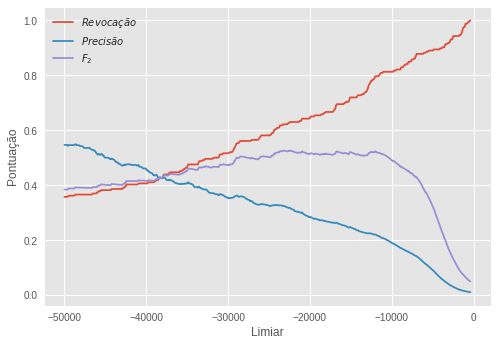
O limiar escolhido foi de -22466.53 e com essa regra de decisão conseguimos a seguinte pontuação:

\[R=0,630 \quad P=0,323 \quad F_2=0,529\]

Podemos notar que esse modelo não bate o nosso benchmark, mesmo sendo capaz de representar qualquer distribuição possível. Isso acontece porque todo esse poder vem a um custo de muitas vezes encontrar superfícies de separação mais complicadas do que elas de fato deveriam ser. Algumas vezes - e provavelmente essa é uma delas - a complexidade adicional tem um custo mais elevado do que o benefício que se ganha com capacidade. Isso é o que chamamos de dilema viés-variância em aprendizado de máquina. Para mais informações sobre isso, temos também esta excelente postagem que cobre de maneira intuitiva o assunto.

Por fim, também é interessante notar como esse modelo peca mais em precisão, tendo uma revocação aceitável.

Modelo de Floresta de Isolação

O modelo de floresta de isolação é outro modelo que podemos considerar como um aproximador universal de distribuições. Assim, não precisamos colocar nenhuma hipótese restritiva na forma como os dados são distribuídos. Esse modelo é baseado em estruturas de árvores, uma classe de métodos de aprendizado de máquina que se popularizou muito nos últimos anos devido a sua simplicidade intuitiva e rapidez de treinamento. O modelo de floresta de isolação ajusta várias árvores de isolação aos dados. Para construir cada árvore de isolação, primeiro selecionamos aleatoriamente uma das variáveis nos dados. Em seguida, selecionamos um valor aleatório entre o máximo e o mínimo dessa variável, que será utilizado para separar os dados. Nós continuamos fazendo essas segmentações aleatórias até que todas as observações estejam isoladas, isto é, separadas das demais. Á primeira vista, pode parecer estranho como essas decisões aleatórias vão nos ajudar a detectar anomalias, mas eis a ideia. Na imagem abaixo, \(X_1\) é uma observação normal e \(X_0\) é uma observação anômala.

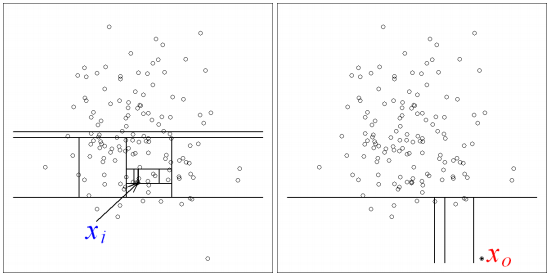
Nossa esperança é que as anomalias sejam distintas dos dados normais, sendo que esses se aglomeram em algum local do espaço, enquanto que aquelas ficam mais isoladas. Assim, será preciso muito menos segmentações aleatórias para isolar uma anomalia do que para isolar uma observação normal. Nós podemos usar o número de segmentações até uma observação ser isolada como uma pontuação de anomalia: quanto maior esse número, menor a probabilidade da amostra ser uma anomalia. Quando construímos várias dessas árvores e combinamos a pontuação de anomalia delas para conseguir uma pontuação final temos uma floresta de isolação. Após treinada, nós utilizamos a subamostra de validação para ajustar o limiar segundo essa pontuação.

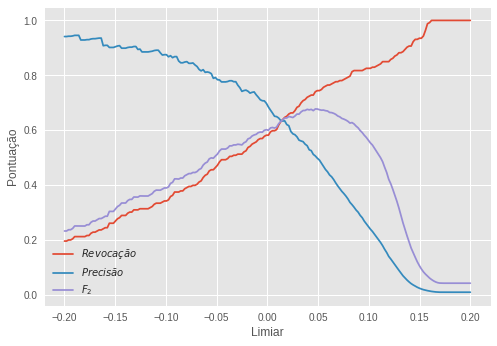
Nosso limiar ótimo foi de 0,049. Com essa regra de decisão, tornamos à subamostra de teste para produzir uma avaliação final. Os resultados foram os seguintes:

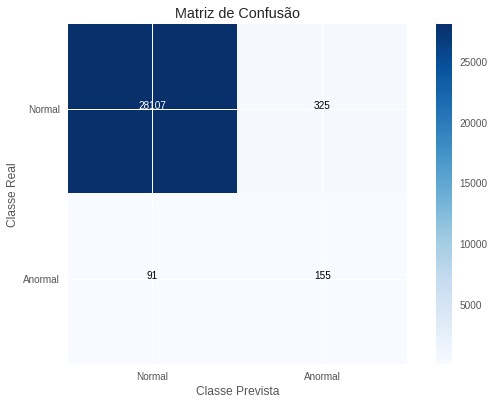
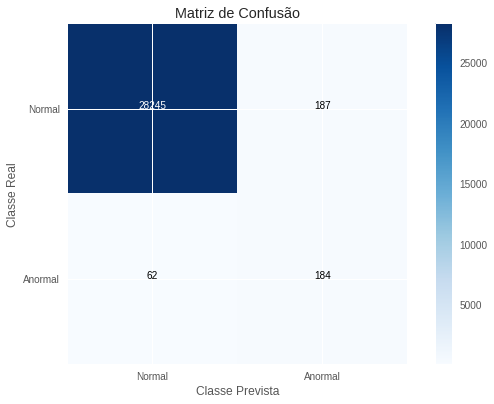
\[R=0,760 \quad P=0,482 \quad F_2=0,681\]

Esses resultados batem o nosso benchmark, mas por pouco. Mais uma vez, notamos que o modelo tem sua performance puxada para baixo pela precisão, sendo que a revocação é bastante boa. Cabe ainda ressaltar que vantagens dessa metodologia frente às máquinas de suporte vetorial são a velocidade de treinamento e a capacidade de fácil paralelização. Como o treinamento de cada árvore é independente das demais, podemos realizá-lo em processos ou máquinas separadas, o que aumenta significativamente a rapidez com que treinamos uma floresta. Para finalizar, colocamos abaixo a matriz de confusão com respeito a avaliação final, na subamostra de teste.

Modelo Neural

Nos últimos anos, redes neurais se tornaram o canivete suíço de aprendizado de máquina, tanto pela sua flexibilidade e efetividade na maioria dos cenários que envolvem problemas estatísticos de alta complexidade e não linearidade. Aqui, nós vamos utilizar um modelo neural chamado autocodificador, no qual pedimos que uma rede neural reconstrua o sinal que lhe é passado. No nosso caso, vamos pedir que ela reconstrua os dados da transação. Para impedir que a rede neural simplesmente copie o que lhe foi passado como reconstrução perfeita, nós colocamos uma camada de neurônios estreita no meio da rede neural. Essa cama terá apenas dois neurônios e como os nossos dados têm 30 variáveis, isso significa que a rede neural terá que aprender uma representação interna que condense 30 dimensões em apenas duas.

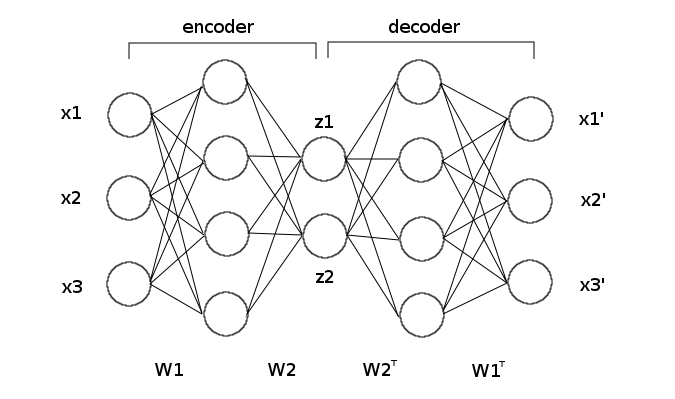
Nós vamos treinar um autocodificador utilizando apenas a subamostra de dados normais. Nossa esperança é que, ao não ser treinada para reconstruir as anomalias, a rede neural fará um péssimo trabalho reconstruindo-as, mas fará um ótimo trabalho reconstruindo observações normais. Assim, podemos usar o erro de reconstrução como uma pontuação para anormalidade: quanto maior o erro, maior a probabilidade da observação ser uma anomalia. Uma vez treinada a nossa rede neural, nós utilizamos a subamostra nomeada de validação para ajustar o limiar quanto à pontuação de anomalia.

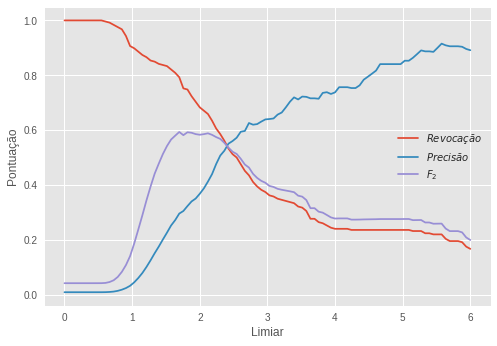
O limiar ótimo foi um erro de 1.69, o que nos deu os seguintes resultados:

\[R=0,813 \quad P=0,294 \quad F_2=0,601\]

Notamos que esse modelo não é melhor que o nosso benchmark e, mais uma vez, a precisão prejudicou a performance do modelo. É necessário observar que o autocodificador não é otimizado para detectar anomalias, mas para reconstruir sinais. Nós suspeitamos que ele seja tão bom nisso que esteja reconstruindo bem tanto o sinal normal quanto o anormal, tornando-o não muito bom para detecção de anomalia. Outro aspecto do autocodificador que merece atenção é que ele funciona como um método de redução de dimensões. Como utilizamos apenas dois neurônios na camada estreita, nós guardamos a atividade neural nessa camada como uma representação reduzida dos dados originais. Mais ainda, como temos apenas duas dimensões nessa versão reduzida, podemos colocá-la em um gráfico:

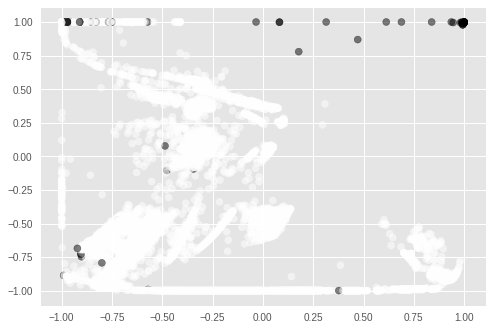
Acima, representamos em branco os pontos normais e em preto, os anormais. É interessante perceber como a maioria das anomalias se agrupam em regiões distintas das regiões de normalidade. Talvez, o autocodificador não devesse ser utilizado como um método de detecção de anomalias em si, mas como um estágio de pré-processamento, onde primeiro conseguiríamos a representação acima e então usaríamos ela em conjunto com algum outro método de detecção de anomalia. Entretanto, isso ficará para um trabalho futuro.

Abaixo, colocamos a matriz de confusão do método neural para detalhar os tipos de erros que ele comete.

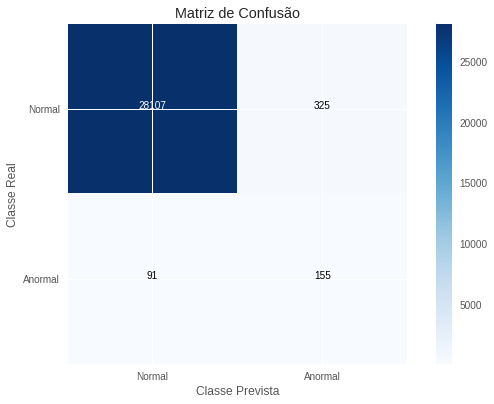
Conclusão

Métodos semi-supervisionados de aprendizado de máquina são excelentes em cenários de detecção de anomalias, em que há pouquíssimos exemplos do caso anômalo. Até agora, não encontramos nenhum projeto (no Kaggle) que apresentasse resultados melhores dos aqui apurados. O melhor modelo que desenvolvemos foi o de mistura de gaussianas com um F2-score de 79%. Entretanto, vale ressaltar que esse método não é universalmente superior. Em problemas de detecção de anomalias, bastante específicas de acordo com o domínio de interesse, é improvável que um algoritmo seja sempre melhor do que outro.

Esse post tratou de detecção de fraudes, mas as técnicas foram desenvolvidas de forma bastante geral para se estenderem a outras aplicações. Algumas delas são: detecção de cartéis, irregularidades em leilões, inadimplência, sonegação e corrupção.