Teste de Eventos

Olá pessoal! Essa semana o LAMFO traz para vocês a metodologia conhecida como Teste de Eventos, com uma breve introdução, referencial teórico e um exercício prático utilizando R.

Durante o dia, é comum ouvirmos ou lermos alguma notícia sobre acontecimentos ou mudanças no país e no mundo. A todo momento recebemos atualizações, novas informações e opiniões a respeito dos mais diversos temas que refletem em nosso comportamento e até planejamento para o futuro. Mas e o mercado? Será que ele também é afetado pela repercurssão desses eventos?

Para responder essa pergunta, foi criado o Teste de Evento (Event Study).

Metodologia

Os autores Campbell, Lo e Mackinley (1997) foram os primeiros a definir e escrever sobre esta metodologia. A idéia básica é observar se o valor de uma empresa é alterado com o aparecimento de um evento, ou seja, se o “retorno normal” esperado sofre alguma “anormalidade”. O desenvolvimento do Teste de Eventos tem como base a Teoria dos Mercados Eficientes de Fama (1970), em que se acredita que o mercado absorve as informações públicas disponíveis e realiza o ajuste do preço dos ativos.

Apresentaremos quatro passos simples para começar nosso Teste de Eventos!

Passo 1: Definição do Evento

Mas de que tipo de evento estamos falando?

Podemos estudar qualquer tipo de evento, contanto que tenhamos suficientes dados e que ele seja publicamente conhecido. Temos por exemplo eventos como:

Distribuição de dividendos;
Fusão e aquisições de outras empresas;
Recompra de ações;
Novas leis e regulamentações;
Privatização ou estatização;
Escândalos políticos.

Uma vez escolhido o evento, é preciso definir uma linha do tempo e as janelas de análise.

Janela de estimação: representa o período em que os retornos normais do ativo serão padronizados, de $T_0$ a $T_1$. Dessa forma, teremos uma base de comparação de retornos que não foram “contaminados” pelo aparecimento do evento.

Janela do Evento: intervalo de tempo em que o evento em questão apareceu. A data que o evento ocorreu é determinada como momento zero ($0$) e a partir desse marco é estabelecido um “intervalo de segurança” para verificar se houve vazamento de informações privilegiadas antes do acontecimento, $T_1$ a $0$, e para englobar o período de absorção do evento pelo mercado, de $0$ a $T_2$.

Um detalhe importante é que não existe um número fixo para esta janela. Podemos, por exemplo, ter três meses antes e depois do evento ou até mesmo quinze dias antes e depois para compor a janela. Uma saída seria realizar uma modelagem e avaliar o erro estatístico.

Janela Pós-Evento: momento após o acontecimento do evento e eventuais movimentações do mercado. É possível observar o impacto do acontecimento a longo prazo.

Passo 2: Empresas

Com as datas determinadas, agora precisamos selecionar quais empresas farão parte do estudo e porque. Normalmente o primeiro filtro é se a empresa que se deseja estudar possui ações na bolsa de valores, uma vez que utilizamos o retorno para nossos cálculos.

Uma ideia para o segundo filtro seria o setor de empresas, por exemplo, se usassemos o Teste de Eventos para verificar o impacto de novas leis ambientais. Nesse caso, seria interessante selecionar empresas do setor de mineração e petróleo.

Agora é preciso coletar os dados dos retornos da empresa ou empresas selecionadas. É importante ressaltar que a unidade temporal dos dados deve ser a mesma, por exemplo, se o evento estudado for registrado em um dia, as oberservações de retorno também devem ser diárias.

Passo 3: Estabelecendo Retornos Normais e Anormais

Como estabelecido na linha do tempo, primeiro estimamos o retorno normal do ativo para depois analisarmos a anormalidade.

Uma base de dado com os retornos da empresa escolhida é o suficiente para iniciar a composição da base de retornos normais. O importante é que a unidade temporal seja a mesma e que as observações se iniciem em $T_0$ e terminem em, pelo menos, em $T_2$.

Para verificar se existem ou não retornos anormais, usaremos a seguinte equação base:

\[Ra_{i,t}=R_{i,t} - \mathbb E[R_i|X_t ]\]

Sendo $Ra_{i,t}$ o retorno anormal, uma vez que será a diferença do retorno real em t ($R_{i,t}$) e do retorno normal esperado em determinado período ($$E[R_i

X_t ]$$).

Como já teríamos a base com os retornos da empresa de $T_0$ a $T_2$, precisamos escolher qual o melhor modelo para se estabelecer o retorno padrão:

Retorno Ajustado a Média
Retorno Ajustado ao Mercado
Modelo de Mercado
Modelos Econômicos

Retorno Ajustado a Média

O retorno normal esperado aqui será definido pela média simples dos retornos reais da janela de estimação ($T_0$ a $T_1$).

\[Ra_{i,t}=R_{i,t} - \overline R_i\]

Uma crítica a esse modelo é que se assume que os retornos terão retornos médios constantes ao longo do tempo. Dependendo da unidade temporal escolhida, este pressuposto por si só já apresenta uma grande margem de erro.

Retorno Ajustado ao Mercado

Neste caso, o retorno normal será definido como o retorno da cateira de mercado ($Rm$). Neste método será necessário obter uma base de dado com os retornos na mesma unidade temporal do ativo referência do mercado (benchmark).

\[Ra_{i,t}=R_{i,t} - Rm_i\]

Modelo de Mercado

A abordagem do Modelo de Mercado possui sua base na estatística, aprimorando as estimativas realizadas anteriormente pelos demais modelos.

Diferente do Modelo de Retorno Ajustado ao Mercado, o Modelo de Mercado não utiliza o retorno de uma carteira referência, mas sim índices como S&P500 para análises norte-americanas ou IBOVESPA para ações nacionais, sendo definido por:

\[Ra_{i,t}=R_{i,t} - \widehat \alpha_i - \widehat \beta_iR_{m,t}\]

No qual o retorno anormal ($Ra_{i,t}$) é definido pelo retorno real do ativo em um período t menos os parâmetros alpha ($\alpha$) e beta ($\beta$) estimados por uma regressão linear da janela de estimação para o índice de mercado.

Por utilizar regressão linear, o ganho e previsão do modelo depende do R$^2$. Quanto maior for este indicador, menor será a variância do do retorno anormal, garantindo uma maior estabilidade ao modelo.

Modelos Econômicos

Com base nas práticas do mercado, se desejamos estimar um valor para o retorno futuro de um ativo existem duas metodologias utilizadas (1) Capital Asset Pricing Model (CAPM) e (2) Arbitrage Pricing Theory (APT). Ambos podem ser utilizados para estimar o retorno normal, porém é preciso ficar atento para os requisitos de cada um, assim como o período da janela de estimação.

Capital Asset Princing Model (CAPM)

\[Ra_{i,t} = R_i - Rf_i - \beta (Rm_i - Rf_i)\]

Em que o retorno anormal é identificado pela diferença do retorno real com o retorno estipulado considerando a sensibilidade do ativo e elementos como retorno de mercado ($Rm$) e de ativos livre de risco ($Rf$).

Arbitrage Pricing Theory (APT)

\[Ra_{i,t} = R_i - R_f + \beta_1 R_1 + \beta_2 R_2 + \beta_n R_n\]

Neste modelo temos um prêmio pelo risco para fatores diferentes, considerando a sensibilidade do ativo ao fator específico. Para adquirir o Beta ($\beta_n$) será preciso realizar uma regressão linear para cada fator e o ativo.

Passo 4: Mensuração e Análise dos Retornos Anormais

Com o modelo definido, agora devemos calcular o comportamento dos retornos. Normalmente, usamos duas métricas para os retornos anormais, o retorno anormal médio da amostra e o retorno anormal acumulado.

Para aceitarmos os resultados, é preciso que o P-Valor do modelo esteja dentro da margem de aceitação ou que o $R^2$ seja o maior possível.

Aplicando o modelo

A aplicação do Teste de Eventos será realizada utilizando o R, com adicionais de alguns pacotes como:

quantmod : coletar os dados de retorno das empresas escolhidas.
eventstudies: pacote específico para utilizar o teste de eventos automaticamente.
zoo: tratamento dos dados da série financeira.
xts: tratamento de dados de séries temporais sem ajustes.

Estouro da Bolha Imobiliaria nos EUA (2008)

Usaremos o pacote de Teste de Eventos já existente no R e depois calcularemos o impacto do evento de maneira manual. Como analisamos um evento de caráter econômico e ligado ao setor imobiliário, procuraremos empresas que sejam cotadas na bolsa de valores brasileira (BM&FBOVESPA) e que atuem no setor. Selecionamos para análise as empresas Gafisa e Cyrela e como parâmetro para o modelo de mercado o índice IBOVESPA.

Teste de Eventos utilizando o pacote eventstudies

O pacote é dividido em etapas, a primeira delas é estabelecer o nome das empresas e a data em que o evento aconteceu. Como o evento é o mesmo para ambas, colocaremos a data “2008-03-13” referente aproximadamente ao dia em que a notícia da bolha veio a público.

#Passo 1: Listar os ativos e datas dos eventos
eventosDatas<-data.frame("name"=c("BVSP","GAFISA","CYRELA"),
                         "when"=c("2008-03-13","2008-03-13","2008-03-13"))

#Passo 2: Converter para texto
eventosDatas$name<-as.character(eventosDatas$name)
eventosDatas$when<-as.character(eventosDatas$when)

#Passo 3: Lista de retornos
BVSP<- read.csv("^BVSP.csv")
BVSP<-BVSP[,c(1,6)]
colnames(BVSP)<-c("Data","BVSP")

GAFISA<- read.csv("GFSA3.SA.csv")
GAFISA<-GAFISA[,c(1,6)]
colnames(GAFISA)<-c("Data","GAFISA")

CYRELA<- read.csv("CYRE3.SA.csv")
CYRELA<-CYRELA[,c(1,6)]
colnames(CYRELA)<-c("Data","CYRELA")

#Passo 4: Junta as bases de dados
dados<-merge(BVSP,GAFISA,by="Data",all=T)
dados<-merge(dados,CYRELA,by="Data",all=T)

#Passo 5: Calcula o retorno
dados$BVSP <- c(NA,diff(log(as.numeric(dados$BVSP)), lag=1))
dados$GAFISA <- c(NA,diff(log(as.numeric(dados$GAFISA)), lag=1))
dados$CYRELA <- c(NA,diff(log(as.numeric(dados$CYRELA)), lag=1))

#Passo 6: Converte em objeto zoo
dados.zoo<-read.zoo(dados)

#Passo 7: Teste de Eventos Market Model
es.mm <- eventstudy(firm.returns = dados.zoo,   #Base de retornos
                     event.list = eventosDatas, #Datas dos eventos
                     event.window = 5,          #Tamanho da janela   
                     type = "marketModel",      #Modelo utilizado
                     to.remap = TRUE,           #Recalculado os retornos usando cumsum
                     remap = "cumsum",          #Testa o evento para o retorno acumulado
                     inference = TRUE,          #Inferência acerca do evento
                     inference.strategy = "bootstrap",   #Boostrap para avaliar o erro-padrão
                     model.args = list(market.returns=dados$BVSP))  #Adiciona a base do índice do mercado IBOVESPA
#Passo 8: Plotar gráfico
plot(es.mm)

#Passo 9: Obersrevar resultados
summary(es.mm)

Como resultado temos:

Event outcome has 3 successful outcomes out of 3 events: 
[1] "success" "success" "success"

Aparentemente o estouro da bolha nos EUA apresentou um impacto no retorno das empresas brasileiras, mas será que o resultado é significante? Para isso vamos observar o gráfico gerado pelo pacote.

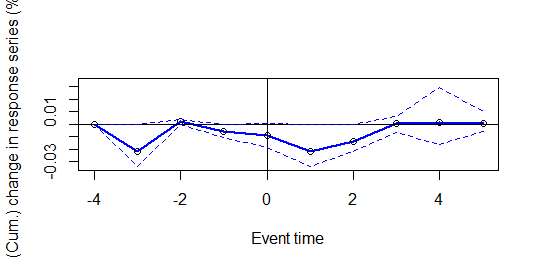
Como podemos constatar, a linha azul (que representa o retorno das ações) está dentro da área de anormalidade (linhas pontilhadas). Porém dentro da janela de 5 dias, os resultados encontram-se diversas vezes em zero. Isso significa que mesmo que o evento aparentemente cause uma anormalidade no retorno, não há comprovação estatística.

Agora vamos comparar o resultado com cálculos a mão!

Teste de Eventos calculado manualmente

rm(list=ls())
library(quantmod)
GFSA<-read.csv("GFSA3.SA.csv")
CYRE<-read.csv("CYRE3.SA.csv")
BVSP<-read.csv("^BVSP.csv")

#Converte para data
GFSA$Date<-as.character(GFSA$Date)
GFSA$Date<-as.Date(GFSA$Date,format="%Y-%m-%d")
GFSA <- xts(GFSA[,-1], order.by=GFSA[,1])

CYRE$Date<-as.character(CYRE$Date)
CYRE$Date<-as.Date(CYRE$Date,format="%Y-%m-%d")
CYRE <- xts(CYRE[,-1], order.by=CYRE[,1])

BVSP$Date<-as.character(BVSP$Date)
BVSP$Date<-as.Date(BVSP$Date,format="%Y-%m-%d")
BVSP <- xts(BVSP[,-1], order.by=BVSP[,1])

#Estouro da bolha imobiliária em 2008
startEvent = as.Date("2008-03-13") 

#Estabelecido intervalo da janela do evento
endEvent = as.Date("2008-03-18") 

#Início da série
startDate<-as.Date("2008-01-01")

#Plota a série temporal dos preços de fechamento ajustado
plot.xts(GFSA$Close,major.format="%b/%d/%Y",
         main="GAFISA",ylab="Adj.Close price.",xlab="Time")

plot.xts(CYRE$Close,major.format="%b/%d/%Y",
         main="CYRELA",ylab="Adj.Close price.",xlab="Time")

#Calcula o log-retorno.
diffGFSA<-diff(log(GFSA$Adj.Close))
diffCYRE<-diff(log(CYRE$Adj.Close))

#Plota a série temporal dos preços de fechamento ajustado
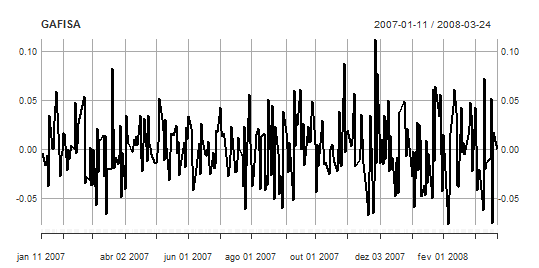
plot.xts(diffGFSA,major.format="%b/%d/%Y",
         main="GAFISA",ylab="Log-return Adj.Close price.",xlab="Time")

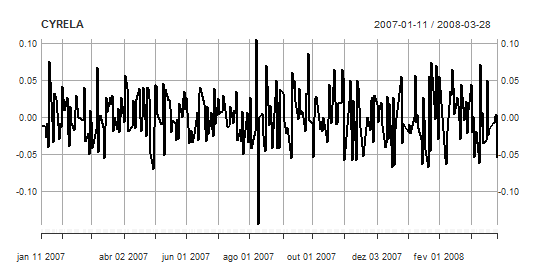
plot.xts(diffCYRE,major.format="%b/%d/%Y",
         main="CYRELA",ylab="Log-return Adj.Close price.",xlab="Time")

#Janela de estimação
GFSASubset<-  window(diffGFSA, start = startDate, end = startEvent-1)
CYRESubset<-  window(diffCYRE, start = startDate, end = startEvent-1)

#BVSP
diffBVSP<-diff(log(BVSP$Adj.Close))
BVSPSubset<-window(diffBVSP, start = startDate, end = startEvent-1)

#Estima o modelo de mercado
MarketModel<-lm(GFSASubset$Adj.Close~BVSPSubset$Adj.Close)
summary(MarketModel)

MarketModel2<-lm(CYRESubset$Adj.Close~BVSPSubset$Adj.Close)
summary(MarketModel2)

#Aplica o Market Model
epsilon<-diffGFSA-coef(MarketModel)[1]-coef(MarketModel)[2]*diffBVSP

epsilon2<-diffCYRE-coef(MarketModel2)[1]-coef(MarketModel2)[2]*diffBVSP

#Encontra a variância do epsilon
BVSPSubset1<-na.omit(window(diffBVSP, start = startDate+1,
                           end = startEvent-1))

X<-as.matrix(cbind(rep(1,length(BVSPSubset1$Adj.Close)),BVSPSubset1$Adj.Close))

BVSPSubset2<-window(diffBVSP, start = startEvent, end = endEvent)

Xstar<-as.matrix(cbind(rep(1,length(BVSPSubset2$Adj.Close)),BVSPSubset2$Adj.Close))

#Calculo para GAFISA
V<-(diag(nrow(X))*var(residuals(MarketModel)))+
  ((X%*%solve(t(Xstar)%*%Xstar)%*%t(X))*var(residuals(MarketModel)))

epsilonStar<-window(epsilon, start = startEvent, end = endEvent)
CAR<-sum(epsilonStar$Adj.Close)
SCAR<-CAR/sqrt(sum(V))

#Calculo para CYRELA
V2<-(diag(nrow(X))*var(residuals(MarketModel2)))+
  ((X%*%solve(t(Xstar)%*%Xstar)%*%t(X))*var(residuals(MarketModel2)))

epsilonStar2<-window(epsilon2, start = startEvent, end = endEvent)
CAR2<-sum(epsilonStar2$Adj.Close)
SCAR2<-CAR2/sqrt(sum(V2))

#Valor crítico da distribuição T
alpha<-0.05
df<-length(GFSASubset$Adj.Close)-2
qt(alpha/2,df)
qt(1-(alpha/2),df)

df2<-length(CYRESubset$Adj.Close)-2
qt(alpha/2,df)
qt(1-(alpha/2),df)

Os resultados para ambas as empresas são de -2.012896 e 2.012896. Como não foram observadas evidências em favor da rejeição da hipótese nula, o evento não possui efeito no retorno dos ativos.

Assim concluímos nosso exercício sobre teste de eventos! Em caso de dúvidas entre contato com o LAMFO!