Incerteza em Modelos de Deep Learning

Conteúdo

1. Introdução
2. Por que Incerteza é Importante
3. Monte-Carlo Dropout: um olhar Bayesiano para Deep Learning
4. Obtendo Incerteza
5. Incerteza em Regressão
6. Incerteza em Classificação
7. Resumindo os Pontos Importantes
8. Referências

Introdução

Acredito que muitos cientistas de dados (eu inclusive) já cometeram o pecado de negligenciar o rigor dos métodos estatísticos, supondo que validação cruzada seria suficiente para qualquer problema. Isso pode ser verdade em situações simuladas e dados de laboratório, mas a vida real é bem mais complexa. A dinâmica da realidade faz com que as distribuições geradoras de dados estejam sempre mudando. O resultado disso é que os dados que usamos durante o treinamento raramente coincidem perfeitamente com os dados onde o modelo deve fazer suas previsões; há quase sempre um ponto cego, uma nova região multidimensional na qual nosso modelo fica simplesmente perdido. Para piorar, a maioria dos modelos de aprendizado de máquina sequer tem um mecanismo para nos dizer quando algo está errado com suas previsões.

Recentemente, decidi dar um passo atrás e encarar os meus modelos sob uma perspectiva mais crítica. Como saber se meu modelo está aprendendo algo estatisticamente razoável? Quão confiável é o meu modelo? Mais importante ainda, como saber se meu modelo não vai quebrar diante de algo muito diferente de tudo que ele já viu? E como proceder diante dessas situações inusitadas? Este post fala principalmente sobre incerteza e sobre como injetá-la em modelos de redes neurais. Trata-se de um tópico ainda bastante obscuro, mesmo para a comunidade de aprendizado de máquina, mas que acredito que deveria ser encarado com mais atenção.

O que tentarei fazer aqui será lhe convencer de que não basta obter a melhor capacidade preditiva; também é preciso construir modelos que saibam nos dizer o nível de confiança de suas previsões. Em seguida, mostrarei uma técnica extremamente simples para obter incerteza em modelos de Deep Learning. Reconheço que este post trata de um conteúdo um pouco mais avançado, mas tentarei torná-lo o mais intuitivo possível. No entanto, ainda precisarei pressupor, por parte do leitor, conhecimento sobre o básico de redes neurais, Teorema de Bayes e conceitos de regularização.

Por que Incerteza é Importante

Digamos que eu treine um modelo de aprendizado de máquina para distinguir entre imagens de cães e gatos. Se eu então pedir que esse modelo classifique a imagem de um cocker spaniel, ele deve me dizer, com grande confiança, que há um cachorro naquela foto. Mas e se eu lhe pedir para classificar um homem? Bom, ele será forçado a prever um cão ou um gato, mas seria bom se também me dissesse que não está nada certo sobre essa previsão.

Troque o exemplo infantil acima por algo mais arriscado, como um carro autônomo, um modelo para diagnóstico de câncer ou um modelo que dá empréstimos automaticamente. Nesses exemplos, o custo de um erro pode ser altíssimo. Aqui, quando diante de um caso estanho, muito melhor seria se, em vez de decidir automaticamente, o modelo nos desse algum sinal sobre sua incerteza, de forma que possamos reagir de acordo, talvez passado a decisão para um humano ou especialista.

Em casos de previsão sobre o futuro, como por exemplo no mercado financeiro, a incerteza também exerce um papel fundamental nas decisões. Um modelo pode prever que uma ação vai subir 20% em 3 meses, mas antes de simplesmente comprá-la é importante saber quão certo o modelo está sobre essa previsão, o que é normalmente representado por um intervalo de confiança. Eu provavelmente tomarei decisões diferentes se meu modelo me disser que a ação vai subir 20%, mas pode ser que ela suba 15% ou 25% (baixa incerteza), ou se ele me disser que ela vai subir 20%, mas pode ser que ela suba 50% ou caia 25% (alta incerteza).

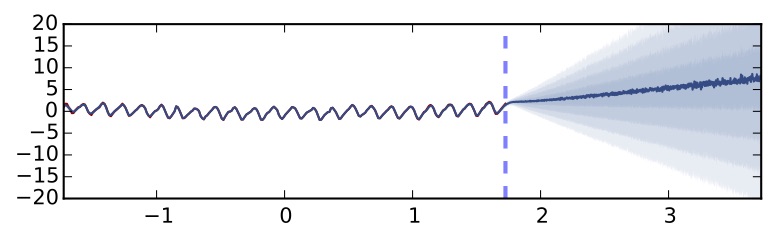
Saber a incerteza do modelo também permite algo que chamamos de Aprendizagem Ativa, onde o próprio modelo nos diz quais dados devemos nomear para retreiná-lo de maneira mais eficiente. Como exemplo, se eu tenho um modelo que atua com seguro de carro e que está muito incerto sobre quanto cobrar de idosos que dirigem sedãs, talvez seja uma boa eu incluir na minha base de treinamento mais exemplos de idosos que dirigem sedãs.

Colocando em termos mais gerais, tão importante quanto saber é saber o que se sabe, isto é, conhecer os limites do próprio conhecimento. É este tipo de meta conhecimento que estamos tentando dar aos nossos modelos quando falamos de muni-los com incerteza. Idealmente, queremos que os sistemas de inteligência que construirmos consigam também reconhecer, por si próprios, as fronteiras de seu conhecimento e responder de acordo com o seu nível de ignorância.

Monte-Carlo Dropout: um olhar Bayesiano para Deep Learning

Em 2015, Yarin Gal mostrou que é possível obter incerteza a partir de redes neurais quase que gratuitamente, se olhássemos técnicas de regularização estocásticas, como Dropout, sob uma perspectiva Bayesiana. Dropout (Srivastava et al, ‎2014) é uma técnica utilizada na maioria das redes neurais modernas para prevenir sobre-ajustamento. Durante o treinamento, Dropout funciona zerando aleatoriamente uma percentagens de neurônios nas camadas da rede neural. No momento de fazer previsões, todos os neurônios são mantidos e a rede neural atua como uma grande mistura de sub-redes menores.

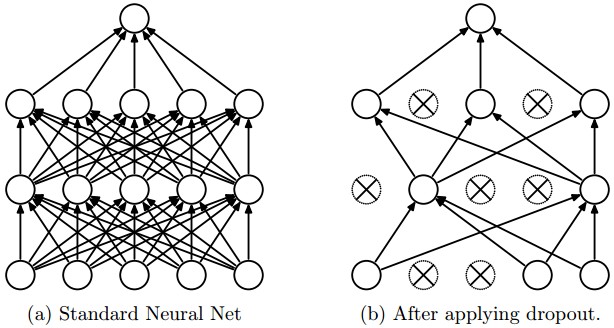
Quando Dropout foi lançado como técnica de regularização, ninguém sabia muito porque ele funcionava tão bem. Em 2015, Gal mostrou que Dropout essencialmente performa otimização Bayesiana na rede neural, marginalizando a incerteza do modelo. A seguir tentarei resumir um pouco dessa teoria. Cuidado! Matemática a frente! Se você não é muito fã de justificativas matemáticas, sugiro que pule para a próxima parte do post. Se fizer isso, você ainda verá como utilizar a técnica, mesmo sem saber porque ela funciona ou como justificá-la.

Sob a perspectiva Bayesiana, os parâmetros \(\pmb{W}\) do modelo são vistos como variáveis aleatórias. Podemos então definir uma distribuição de probabilidade \(P(\pmb{W})\) a priori para esses parâmetros. Sendo a verossimilhança \(P(\pmb{Y}|\pmb{W},\pmb{X})\), pelo Teorema de Bayes temos que a distribuição dos parâmetros dado o que foi observado nos dados é

Note que, desta forma, uma previsão é definida como uma distribuição e a incerteza pode ser entendida como a dispersão desta distribuição.

O problema é que a distribuição a posteriori \(P(\pmb{W}|\pmb{X}, \pmb{Y})\) é praticamente impossível de computar. Isso porque estimar o componente normalizador (também chamado de evidência do modelo) \(P(\pmb{Y}|\pmb{X})\) envolve computar uma integral que não pode estimada eficientemente.

Para lidar com esse problema, definimos uma nova probabilidade mais simples \(q_\theta(\pmb{W})\), parametrizada por \(\theta\), e minimizamos a divergência de Kullback-Leibler entre \(q_\theta(\pmb{W})\) e \(P(\pmb{W}|\pmb{X}, \pmb{Y})\). Isso é equivalente a maximização do limite inferior da evidência (ELBO)

Para facilitar, nós aproximamos o primeiro termo acima com integração de Monte-Carlo, retirando amostras \(\hat{\pmb{W}} \sim q_\theta(\pmb{W}) \)

Normalmente, definimos nossa probabilidade a priori como uma gaussiana centrada em zero \(P(\pmb{W}) \sim \mathcal{N}(0, \sigma)\), o que faz com que o segundo termo aja como um regularizador, mantendo os parâmetros pequenos. Mas e \(q_\theta(\cdot)\)? Uma forma de defini-la é por meio de uma distribuição Bernoulli, onde retiramos um vetor \(\pmb{z} \sim \mathcal{B(\theta)}\) com o mesmo número de elementos que colunas em \(\pmb{W}\). Então podemos definir uma amostra \(\pmb{\hat{W}}\) como a multiplicação de cada elemento de \(\pmb{z}\) por uma coluna de uma matriz de parâmetros \(\pmb{M}\), com as mesmas dimensões de \(\pmb{W}\). Em outras palavras, a nós estamos zerando algumas colunas de \(\pmb{M}\) para obter \(\pmb{\hat{W}}\). Isso soa familiar???

Toda a matemática acima é bastante complexa, mas se olharmos com calma podemos resumi-la em um algoritmo de otimização com dois passos bastante simples:

1. Aleatoriamente, zere colunas de \(\pmb{M}\) para obter \(\pmb{\hat{W}}\).
2. Minimize por uma iteração \(- \log P(\pmb{Y}|\pmb{X}, \pmb{\hat{W}}) - KL(q_\theta(\pmb{W})||P(\pmb{W}))\)

Caso você ainda não tenha percebido, isso é exatamente o que fazemos quando treinamos uma rede neural com Dropout e regularização \(L_2\). Alias, olhe novamente para o passo 2 e repare que o primeiro termo é a tradicional função custo que otimizamos com gradiente descendente e o segundo termo é análogo a regularização \(L_2\). Isso significa que qualquer rede neural treinada com Dropout é um modelo Bayesiano! Isso também explica porque Dropout costuma ser tão efetivo no treinamento de redes neurais: essa técnica equivale a integrar os parâmetros do modelo.

Obtendo Incerteza

Agora que temos um fundamento teórico sólido para seguir, resta ver como obter incerteza a partir de redes neurais treinadas com Dropout (e regularização \(L_2\)). Durante o treinamento do modelo, nada muda; mas, durante o teste mantemos a probabilidade de Dropout fixada durante o treino e realizamos \(T\) forward-pass pela rede, coletando assim \(T\) previsões \(\hat{y}\) para cada amostra. Assim para cada ponto teremos uma previsão para a média e uma previsão para a variância, que será nossa medida de incerteza.

Onde \(\tau = \frac{l^2 p}{2 N \lambda}\) é uma medida de precisão, \(p\) é a probabilidade de Dropout, \(\lambda\) é a força da regularização \(L_2\), \(l\) define a nossa crença a priori da escala de \(\pmb{W}\) e \(N\) é a quantidade de dados. Note que \(\tau\) é negligenciável quando há muitos dados, isto é, quando \(N \rightarrow \infty\). Em Python, isso se traduz para umas poucas linhas de código

l = 10
tau = l**2 * (1 - p_dropout) / (2 * X_train.shape[0] * lbd)

y_hat_mean = np.mean(y_hat, axis=1)

y_hat_variance = np.var(y_hat, axis=1)
y_hat_variance += tau**-1

Incerteza em Regressão

Vamos ver como a técnica apresentada acima lida com um problema de regressão. A seguir, vamos tentar prever a quantidade de bicicletas alugadas na hora seguinte, dada as quantidades de bicicletas alugadas nas últimas 10 horas. Para maior conveniência, coloquei o código todo aqui e focarei apenas nas parte mais interessantes para não estender demais este post.

Vamos usar o pacote Keras com TensorFlow para construir e rodar a rede neural do nosso experimento. Nossa rede neural terá apenas 2 camadas ocultas, cada uma com 100 neurônios. Utilizaremos uma camada de Dropout após cada camada oculta, zerando 50% das unidades. Também colocaremos uma camada de Dropout logo no começo da rede, mas como temos poucas variáveis, a probabilidade de zerar as unidade aqui será apenas 5%.

from keras import backend as K
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.optimizers import Adam
from keras.regularizers import l2

n_input = X.shape[-1] # n de variáveis
num_out = 1 # n de previsões

p_dropout = 0.5 # probabilidade de Dropout
lbd = 1e-4 # força da regularização L2

model = Sequential()
model.add(Dropout(.05, input_shape=(n_input,)))
model.add(Dense(100, activation='relu', input_shape=(n_input,), kernel_regularizer=l2(lbd)))
model.add(Dropout(p_dropout))
model.add(Dense(100, activation='relu', kernel_regularizer=l2(lbd)))
model.add(Dropout(p_dropout))
model.add(Dense(num_out, activation=None))
model.summary()

opt = Adam(lr=1e-3)
model.compile(loss='mean_squared_error',optimizer=opt)

Definido nosso modelo, podemos treiná-lo. Cada mini-lote terá \(\frac{1}{5}\) das amostras e assim treinaremos por 3000 épocas ou 15000 iterações.

epochs = 3000
model.fit(X_train, y_train,
            batch_size=X_train.shape[0] // 5,
            epochs=epochs,
            verbose=0)

Após o treinamento, a performance do nosso modelo no set de treino é \(R^2=0.73\) e no set de teste, \(R^2=0.77\).

from sklearn import metrics

y_hat_train = model.predict(X_train)
print(metrics.r2_score(y_train, y_hat_train))

y_hat_test = model.predict(X_test)
print(metrics.r2_score(y_test, y_hat_test))

0.729823
0.775525

Acima, a previsão é feita da forma tradicional, isto é, colocando a probabilidade de Dropout em 0%, usando assim toda a capacidade da rede. Esse é o padrão do Keras e precisaremos rescrevê-lo para implementar Monte-Carlo Dropout, no qual mantemos as probabilidades de Dropout de treino também durante as previsões. Abaixo, vamos definir uma função que retornará a última camada da rede, (as previsões) dada a camada de entrada (as variáveis). Além disso, vamos definir que está função será usada tal como durante o treinamento, passando K.learning_phase().

T = 1000
predict_stochastic = K.function([model.layers[0].input, K.learning_phase()], [model.layers[-1].output])

y_hat_mc = np.array([predict_stochastic([X_test, 1]) for _ in range(T)])

y_hat_mc = y_hat_mc.reshape(-1,y_test.shape[0]).T
y_hat_mc.shape

(500, 1000)

Como podemos ver, agora temos 1000 previsões para cada ponto no set de teste. Podemos então obter a média e a variância dessas previsões

l = 10
y_hat_test_mean = np.mean(y_hat_mc, axis=1)
y_hat_test_variance = np.var(y_hat_mc, axis=1)
tau = l**2 * (1 - p_dropout) / (2 * X_train.shape[0] * lbd)
y_hat_test_variance += tau**-1

metrics.r2_score(y_test, y_hat_test_mean)

0.91519

Note como a performance de teste melhorou com esse procedimento. Mais ainda, agora temos uma métrica de incerteza para cada ponto e podemos ver onde o modelo não sabe bem o que está acontecendo. Também podemos plotar as previsões contra os valores observados e colocar um intervalo de confiança em torno das previsões. Abaixo, mostramos as últimas 200 horas do set de teste. Em torno da linha de previsões, colocamos 4 tons de roxo, cada tom denotando meio desvio padrão.

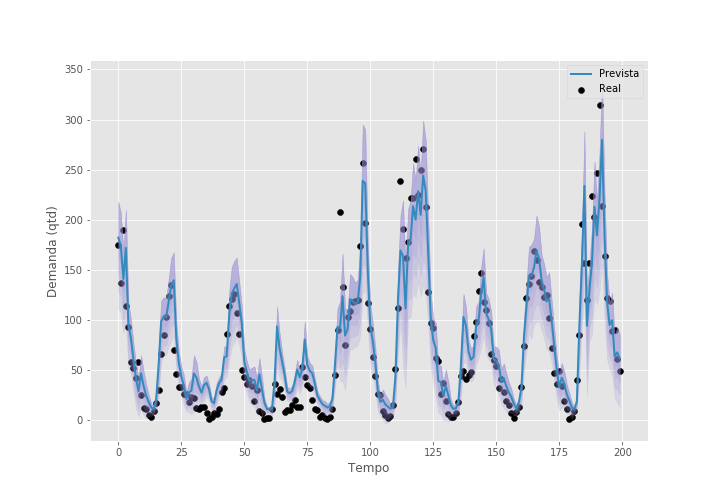
Incerteza em Classificação

Em problemas de classificação estamos tentando estimar a probabilidade de uma amostra \(\pmb{x}\) pertencer às classes \(\pmb{y}\). Um erro que muitos praticantes cometem é supor que a probabilidade de pertencer a classe \(c\), \(P(y = y_c)\), produzida pelo modelo é equivalente a sua confiança. O que devemos lembrar é que, assim como modelos de regressão prevem o valor esperado de uma amostra, condicionado nos seus covariantes \(\pmb{x}\), modelos de classificação prevem uma probabilidade esperada mas, normalmente, nada nos dizem sobre quão dispersa é essa estimativa.

Para melhor entender a diferença entre incerteza a probabilidade prevista, vamos usar parte da base MNIST, da qual vamos filtrar os números 3, 4 e 5. Vamos treinar uma rede neural para distinguir os 5s dos 3s. Será portanto, um problema de classificação binária, onde, nesse caso, 3 será a classe 1 e 5 será a classe 0. Depois disso, mostraremos ao modelo os 4s, nos quais ele não foi treinado. O código muda muito pouco do exemplo de regressão acima, por isso vou omiti-lo. Caso queira conferi-lo, todo esse experimento está disponível no meu GitHub.

A rede neural utilizada aqui foi de duas camadas densamente conectadas, cada uma com 512 neurônios e camadas Dropout após as camadas ocultas e de entrada. A probabilidade de Dropout em todas as camadas foi de 50%. Após treinada, realizamos 1000 forward-passes pela rede para obter as estimativas de Monte-Carlo Dropout. A probabilidade média dessas 1000 estimativas será nossa previsão final e o desvio padrão será nossa métrica de incerteza.

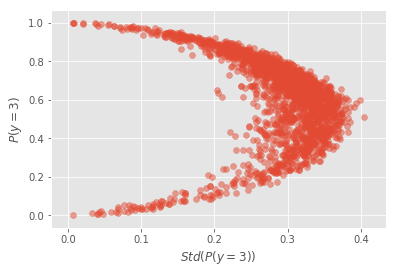
A incerteza média do modelo, computada nos 5s e 3s de teste, é de 0.05. Podemos também plotar \(P(y=3)\) conta o desvio padrão dessa probabilidade. Isso deixará claro que incerteza e probabilidade prevista, embora relacionadas não são a mesma coisa.

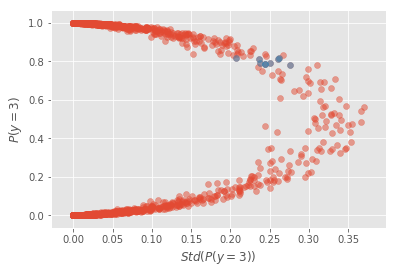
No gráfico acima, note como há pontos que o modelo prevê como sendo um 3 com 80% de chance, mas, para essa mesma probabilidade prevista, existem amostras com incertezas variando de 0.2 até 0.27 (pontos azuis). A variação na incerteza é ainda maior nas probabilidades previstas muito baixas ou altas. Note como há muitos pontos cuja probabilidade prevista é maior que 95% (ou menor que 5%) e como a incerteza nesses pontos varia de 0 até 0.1. Por fim, vale ressaltar que, embora diferentes, probabilidade prevista é incerteza estão relacionadas. Se não fosse o caso, não haveria nenhuma tendência no gráfico acima. O que podemos ver é que a incerteza tende a aumentar perto da fronteira de decisão, isto é, perto dos lugares onde a probabilidade prevista é 50%.

Acima, só analisamos a incerteza do modelo nas imagens de dígitos que ele viu durante o treinamento (3 e 5), mas o que aconteceria se lhe mostrássemos imagens com dígitos 4? Sabemos que ele terá que prever para essas imagens a probabilidade delas ser um 3, afinal é para isso que ele foi treinado, mas queremos que ele faça isso ao mesmo tempo que nos diz estar bastante incerto sobre essas previsões. Isso de fato acontece!

A incerteza média do modelo, quando computada nos 4s, é de 0.28, que é bem maior do que a média de 0.05 obtida no set de teste de 5s e 3s. Além disso, quando plotamos a probabilidade prevista contra o desvio padrão dessas probabilidades, podemos ver que a maioria dos pontos está mais para a direita, reforçando a incerteza geral do modelos ao tentar prever os 4s.

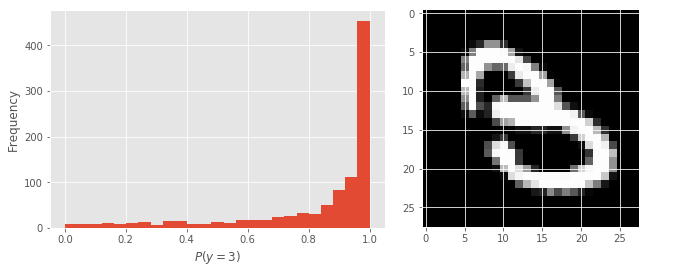
Outro aspecto interessante de Monte-Carlo Dropout é que podemos estudar as incertezas particulares a cada amostra. Por exemplo, abaixo pegamos uma amostra qualquer dos dados de teste (5s e 3s) e plotamos o histograma das probabilidades previstas. Note como na maioria das estimativas de Monte-Carlo Dropout o modelo dá a essa imagem uma probabilidade de 1, indicando que há uma alta chance dela ser um 3. Nesse exemplo particular, o desvio padrão é 0.12.

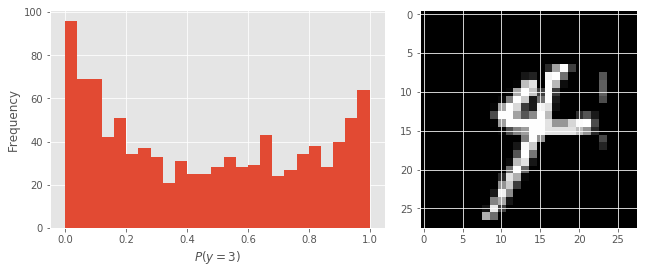
Podemos também ver o que acontece quando mostramos um 4 ao modelo. Note como, desta vez, as probabilidades previstas estão muito mais dispersas. O modelo acha que isso é um 5, já que a maioria das probabilidades previstas são menores que 0.5. Ao mesmo tempo, ele não está nem um pouco certo dessa previsão. Nesse caso particular, o desvio padrão das previsões é de 0.45.

Resumindo os Pontos Importantes

Métricas incerteza podem ser extremamente úteis no processo de tomada de decisão. Por exemplo, é possível estabelecer um limite máximo de incerteza que se está disposto a tolerar. Além disso, com informações sobre incerteza por amostra podemos definir quando é necessário ir atrás de mais informações antes de tomar uma decisão. Também podemos utilizar incerteza para realizar aprendizagem ativa, na qual o modelo nos diz quais dados devem ser nomeados e colocados no set de treino.

Além de saber o que o modelo prevê para uma amostra, Monte-Carlo Dropout nos permite saber qual a certeza que o modelo tem sobre essa previsão. Em aplicações de regressão, isso nos permite traçar um intervalo de confiança em torno do valor previsto. Nos casos de classificação, vimos que incerteza e probabilidade prevista são diferentes, embora relacionadas. A primeira deve ser entendida como uma média de centralidade das previsões enquanto a segunda nos mostra como é a dispersão das probabilidades em torno desta previsão.

Referências

Este post é baseado no trabalho de Yarin Gal sobre incerteza em modelos de Deep Learning. Para este post, usei informações de sua tese de doutorado, Uncertainty in Deep Learning (Gal, 2015), seu artigo Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning (Gal & Ghahramani, 2015) e um post fantástico do seu blog, What my deep model doesn’t know….

Se você está interessado em saber mais sobre abordagens Bayesianas para Deep Learning, o curso Bayesian Methods for Machine Learning acabou se ser lançado no Coursera. Além disso, no NIPS de 2016 houve um workshop dedicado exclusivamente a Deep Learning Bayesiano. Por fim, sugiro que de uma olhada na biblioteca de programação Edward. Ela é construída em cima do TensorFlow e conta com a maioria dos modelos Bayesianos usados atualmente.

O código utilizado neste post pode ser integralmente conferido no meu GitHub.

• ← Previous Post
• Next Post →