Otimização de Estruturas de Filas
As filas são onipresentes, as pessoas assumem os seus lugares e esperam a sua vez. Essa forma de organização tão comum e onerosa é necessária para organizar demandas que são maiores que a capacidade de prestação do serviço. A Teoria das Filas, tenta através de análises matemáticas detalhadas encontrar um ponto de equilíbrio que satisfaça o cliente, e seja viável economicamente para o provedor do serviço de atendimento.

A teoria fornece ferramentas de análise que permitem avaliar, por exemplo, se o tempo médio de espera por atendimento está acima do suportável, o tempo médio de ociosidade dos atendentes, tamanho médio da fila, tempo médio de atendimento. Com variáveis de controle é possível criar benchmarks com o cenário planejado, e realizar melhores tomadas de decisões e alocação de recursos. Existem muitos trabalhos atuais aplicando a teoria das filas, a maioria das quais tem sido documentadas na literatura de probabilidade, pesquisa operacional, controle de qualidade e engenharia industrial. Alguns exemplos são fluxo de tráfego (veículos, pessoas, comunicações, etc), escalonamento de leitos em hospitais, etc.
Historia da Teoria das Filas
Os estudos das filas foram iniciados pelo dinamarquês Erlang que publicou seu primeiro trabalho em 1909 aplicando a teoria de probabilidade ao problema de tráfego de linhas telefônicas. O objetivo inicial foi estudar o congestionamento e os tempos de espera que ocorriam no momento em que as ligações telefônicas eram realizadas. Com a análise dos problemas de tráfego de ligações e utilizando a teoria de probabilidades nesse estudo, Erlang prova o Processo de Poisson para a distribuição aleatória dos tempos entre as chegadas ao sistema.
Passados os anos, os trabalhos de Kendall e Lindley tiveram grande destaque sobre a teoria das filas. Os objetivos eram determinar o tamanho máximo admissível para a fila, a disciplina e o tempo de espera adequados. Para isso, o sistema seguia pressupostos Markovianos, cujo modelo admite que a entrada de dados são independentes e aleatórios.
Na decada de 60 Little criou sua lei. A lei de Little prova matematicamente que uma estrutura de espera é um processo markoviano de tempo continuo em que as transições de estado são de apenas dois tipos: “nascimentos”, que aumentam a variável de estado em um, e “mortes”, que diminuem o estado em um. Ou seja, um novo cliente no sistema representa um nascimento, e a saída do sistema representa uma morte. Um sistema é dito em equilibrio quando o número de entradas é igual a saída de individuos.
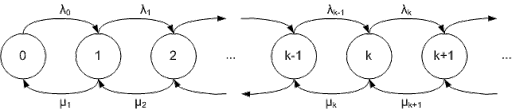
Entendendo a Metodologia
Os tipos de modelos de filas é definido a partir da Notação de Kendall, que representa cada cadeia de filas pelos símbolos \(A\), \(B\), \(c\), \(K\), \(N\), \(Z\) da seguinte forma:
$$A/B/c/K/N/Z$$
- \(A\): distribuição do tempo entre chegadas;-
- \(B\): disciplina de serviços;
- \(c\): número de servidores;
- \(K\): capacidade total de usuários no sistema;
- \(N\): número de usuários potenciais em uma população fonte;
- \(Z\): disciplina de atendimento.
Usualmente, quando não declarado a capacidade máxima do sistema (\(K\)), e o número de clientes a serem atendidos (\(N\)), estes serão considerados como ilimitados.
A disciplina de atendimento pode admitir duas politicas. First In First Out (primeiro que entra primeiro a sair), ou fila, é a estrutura de atendimento que bancos e hospitais utilizam pois sequem a ordem de chegada em que os primeiros a chegarem serão os primeiros a serem atendidos. Last In First Out (último que entra primeiro a sair) é a estrutura habitualmente chamada de pilha e amplamente utilizada na estacagem de produtos. Caso o modelo não declare qual a disciplina de atendimento, entende-se que será utilizada a disciplina FIFO.
Equações de Little
Little utilizando o conceito do processo de nascimento e morte desenvolveu equações teóricas que calculam o desempenho de uma estrutura de espera. Para o modelo $m/m/c$, o número de atendentes é restrito igual a c. Para simplificar a visualização utilizei a notação \(r = \frac{\lambda}{\mu}\) e \(p = \frac{\lambda}{c\mu}\):
Probabilidade do sistema estar vázio
\[P_0=\left ( \sum^{c-1}_{n=0} \frac{r^n}{n!} + \frac{r^c}{c!(1-p)} \right ) ^{-1} , p<1.\]Probabilidade do sistema possuir n clientes
\[P_n= \frac{\lambda^n}{n!\mu^n}P_0, \quad 1 \leq c,$\] \[P_n = \frac{\lambda^n}{c^{n-c}\mu^n}, \quad n \geq c.\]Tempo médio de cada cliente na fila
\[W_q = \frac{r^c}{c!(c\mu)(1-p)^2}P_0\]Número médio de clientes na fila
\[L_q = \frac{r^cp}{c!(1-p)^2}P_0\]Número médio de clientes no sistema
\[L = \frac{r^cp}{c!(1-p)^2}P_0+r\]Tempo médio de cada cliente no sistema
\[W = \frac{1}{\mu}+\frac{r^c}{c!(c\mu)(1-p)^2}P_0\]O modelo \(M/M/1\) da notação de Kendall é a parametrização mais simples, e mais utilizada para um modelo de fila Markoviana. Neste caso, a distribuição do tempo entre novas chegadas de clientes ao sistema é suposta exponencial (\(M\)). O tempo necessário para realizar cada serviço também segue uma distribuição exponencial (\(M\)). A capacidade máxima do sistema e a população fonte são supostamente infinitas. Nas aplicações desse modelo, denotamos por $\lambda$ e $\mu$ a taxa média de chegada e de atendimento, respectivamente. Além disso, supomos que há apenas um servidor e que a disciplina da fila é FIFO.
A relação entre o tempo médio de chegada e de serviço são as medidas de desempenho do sistema. O pressuposto necessário para a validade da teoria de filas , \(\frac{1}{\mu}$ $\leq\) \(\frac{1}{\lambda}\), torna o modelo convergente.
Aplicação
Via linguagem R, veja também outros artigos [1], [2], é possível entender como a teoria se comporta com em relação a dados empíricos. Elaborei um algoritmo que simule um sistema real de filas utilizando a parametrização m/m/1.
options(scipen=999)
library('tidyverse')
#T: período total de simulação;
#tci: instante de tempo em que ocorre a i-ésima chegada;
#tce: tempo entre as chegadas
#tai: instante de tempo em que ocorre o i-ésimo atendimento;
#to: tempo total de ociosidade do servidor;
#te: tempo total de espera na fila;
#tme: tempo médio de espera na fila;
#i: contador;
#t: variável de controle (tempo)
#lambda - Numero medio de clientes que entram/tempo (Poisson)
#1/lambda - Tempo entre clientes (Exponencial)
#mu - Numero de atendimentos desejados/h (Poisson)
#1/mu - Tempo de cada atendimento (Exponencial)
# mi>lambda para que o modelo seja convergente.
simula <- function(tempo,lambda,mu,seed=round(runif(1,min=1,max=2000))){
set.seed(seed)
T <- tempo
t=0
i=1
tc=NULL
tec=NULL
#Gera o vetor, dist.exponencial ,tempo entre as chegadas
while (t < T){ # o algoritmo simula uma linha temporal
tec[i] = (-(1/lambda))*log(runif(1)) #gerador de numeros pseudo-aleatrios
tc[i] = sum(tc[i-1]) + tec[i]
t=tc[i]
i=i+1
}
ta <- NULL
#Gera o vetor, dist.exponencial ,tempo de atendimento
for(i in 1:length(tc)) {ta[i] <- (-(1/mu))*log(runif(1))}
to = tc[1]
te = 0
i = 1
t = tc[1]
n=length(tc)-1
m=0
while (i < n){
if((t+ta[i]) < tc[i+1]){
to=to+tc[i+1]-(t+ta[i])
t=tc[i+1]
if(m >= 0){
m=m-1
}
}
else{
te=te+(t+ta[i])-tc[i+1]
t=t+ta[i]
m=m+1
}
i=i+1
}
tp_espera <-te/n;
prop_ocioso <-to/T;
return(list(W_q=tp_espera,
P_0=prop_ocioso,
L_q=n/tempo))
}
Escrevendo as equações de Little na linguagem R
equacoes_little <- function(m,lambda,mu){
# taxa de eficiencia
p = lambda / (m * mu)
# probabilidade do sistema estar sem clientes
i = c(0:(m-1))
first = sum( (m * p) ^ i / factorial(i) )
p_0 = 1 / ( first + (m * p) ^ m / ( factorial(m) * (1-p) ) )
# tamanho medio da fila de espera
L_q = p_0 * ( ((m^m) * p^(m+1)) / (factorial(m) * (1-p)^2) )
# tempo medio gasto na fila de espera
W_q = L_q / lambda
# tempo medio gasto pelo cliente no sistema
W = W_q + 1 / mu
# Numero medio de clientes no sistema
L = L_q + lambda / mu
return(list(eficiencia=p,
p_0=p_0,
L_q=L_q,
W_q=W_q,
W=W,
L=L))
}
Análise da simulação do modelo \(m/m/1\)
Supondo uma situação real em que um gestor necessita de auxilio de dados nas tomadas de decisões sobre uma estrutura de filas. Por exemplo, coletando os dados da fila de atendimento ele quer avaliar o desempenho do sistema. As variáveis preliminares escolhidas são: o tempo médio que cada cliente passa na fila, a probabilidade do atendente estar ocioso e o tamanho médio da fila durante 60h e 120h de funcionamento. Pelos cálculos, a taxa média de chegada de novos clientes é igual 10/h e tempo médio de serviço igual a 11/h, com apenas 1 atendente.
Parâmetros:
\(\lambda = 10/h;\)
\(\mu = 11/h;\)
\(c = 1\) servidor.
| Variáveis | Simulação (60,10,11) | Simulação (120,10,11) | Teórico (10,11,1) |
|---|---|---|---|
| \(W_q\) | 1.1148517 | 0.878 | 0.909 |
| \(P_0\) | 0.0620553 | 0.0841 | 0.090 |
| \(L_q\) | 10.1500000 | 10.080 | 9.090 |
Além disso, o gestor deseja análisar a distribuição de probabilidade da quantidade de clientes no sistema. Ele deseja ajustar o sistema para que a fila seja em torno de 5 pessoas.
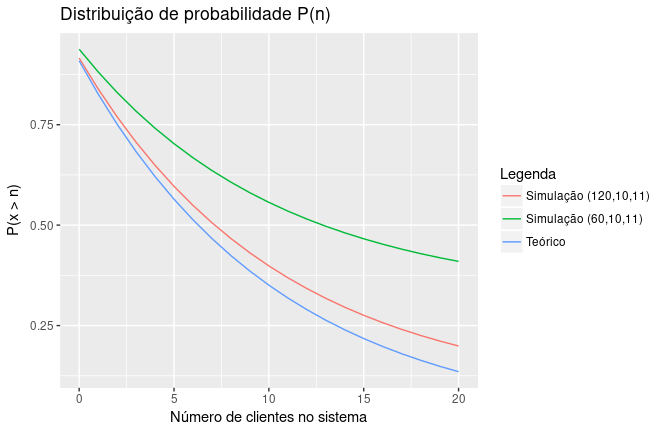
A probabilidade do sistema possuir mais de 5 clientes está acima dos padrões aceitaveis, então percebeu a necessidade de aumentar a quantidade de atendentes. Utilizando as equações de Little, é possível simular qual seria a melhora na performance caso contratasse novos atendentes. Os resultados obtidos considera que todos atendentes apresentam a mesma eficiência no atendimento.
| 1 Atendente (atual) | 2 Atendentes | 3 Atendentes | |
|---|---|---|---|
| eficiencia | 0.909 | 0.455 | 0.303 |
| \(P_0\) | 0.091 | 0.375 | 0.400 |
| \(L_q\) | 9.091 | 0.237 | 0.031 |
| \(W_q\) | 0.909 | 0.024 | 0.003 |
| \(W\) | 1.000 | 0.115 | 0.094 |
| \(L\) | 10.000 | 1.146 | 0.940 |
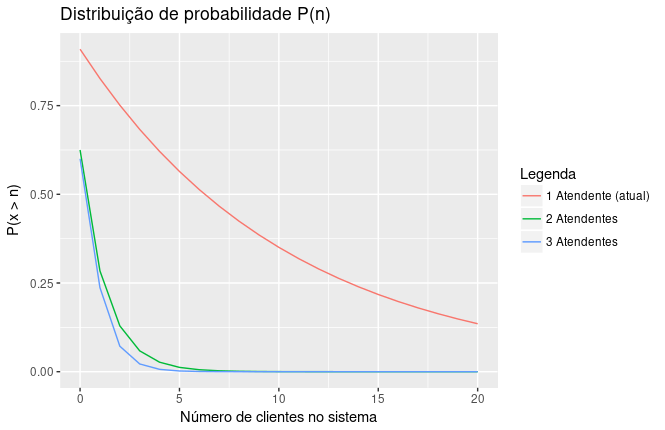
O sistema com dois atendentes torna o sistema dentro dos padrões desejados e deixa claro a não necessidade de possuir 3 atendentes. O novo sistema apresenta a probabilidade do sistema estar vázio no momento da chegada de novos clientes de 0,45%, a chance do sistema atingir 5 pessoas é baixa, e o tempo de espera médio próximo de 0.
Referências
D.G Kendall - Stochastic processes occurring in the theory of queues and their analysis by the method of the imbedded Markov chain
D.V Lindley - The theory of queues with a single server
N. K. Jaiswal - Priority queues