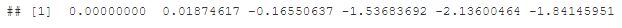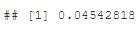Cálculo Estocástico

O cálculo estocástico fornece uma teoria de integração a ser definida para integrais de processos estocásticos em relação a processos estocásticos. É a parte de cálculo dos processos estocásticos que consiste em um evento de interesse que se desenvolve no tempo de uma maneira que (pelo menos) uma componente do processo é aleatória. Portanto, trata-se de uma coleção de variáveis aleatórias indexadas pelo tempo. É usado para modelar sistemas e processos que se comportam aleatoriamente ao longo do tempo.

A maioria dos problemas reais são modelados utilizando processos estocásticos de tempo contínuo (a variável pode mudar o seu valor em qualquer momento de tempo) com variável contínua. Esse tipo de processo exige o uso do cálculo para a resolução de equações diferenciais estocásticas que modelam tais processos. Além disso, eles podem ser aproximados através de processos discretos, cuja modelagem é mais simples.

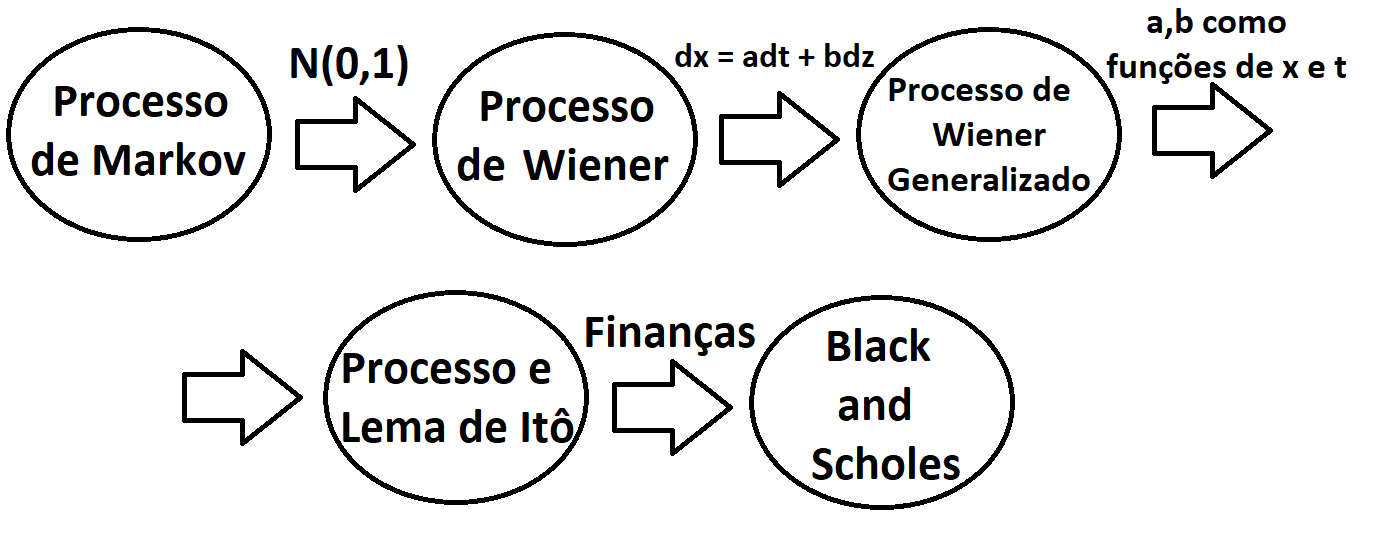
Existem diversos processos e vamos explorar os mais conhecidos e utilizados que irá desde o random walk até a aplicação de Itô na fórmula de Black and Scholes amplamente utilizada e conhecida em finanças. O post segue com a seguinte estrutura.

Processo de markov;
Random walk;
Processo de Wiener;
Processo de Wiener Generalizado;
Lema e Cálculo de Itô;
Black and Scholes;
Aplicação e simulação dos Processos.

Processo de markov

O Processo de Markov é um processo estocástico onde somente o valor atual da variável é relevante para predizer a evolução futura do processo (depende apenas de 1 momento já realizado). Valores históricos (caminho realizado) através do qual a variável atingiu o seu valor atual são irrelevantes para a determinação do seu valor futuro. Nesse modelo, assumimos que o preço atual de uma ação reflete todas as informações históricas bem como as expectativas a respeito do preço futuro desta ação.

Definição: Um processo estocástico discreto é um processo de Markov se

\[P(X_{t+1} = S / X_0, X_1, \cdots, X_t) = P(X_{t+1} = S /X_t)\]

para todo $t ≥ 0$ e $S$.

Geralmente, o processo é totalmente descrito pela matriz de probabilidade de transição A que indica todas as probabilidades de sair de um estado i para j, em 1 passo. A partir da matriz A é possível calcular as probabilidades de transição em mais passos até a sua convergência no limite.

Random walk

Random Walk é um processo de Markov em tempo discreto que tem incrementos independentes e estacionários na forma de:

\[S_{t+1} = S_{t} + \epsilon_t\]

no qual $S_0= 0$, $S_t$ é o valor da variável no tempo t e $\epsilon_t$ é uma variável aleatória com probabilidade P($\epsilon_t$= 1) = P($\epsilon_t$= -1) = 0.5.

O Random Walk pode incluir um termo de crescimento/decrescimento, ou “drift”, que representa um crescimento/decrescimento de longo prazo. Sem o termo de drift, a melhor estimativa do próximo valor da variável $S_{t+1}$ é o seu valor atual (markov), uma vez que o termo de erro é normalmente distribuído com média zero. Com o termo de drift os valores futuros da variável tendem a crescer de maneira proporcional a taxa de crescimento.

Processo de Wiener (Movimento Browniano)

O processo de Wiener é um processo estocástico de tempo contínuo, chamado também de movimento browniano pela a sua relação com o processo físico observado por Robert Brown. É um processo de Lévy que ocorre frequentemente em matemática pura e aplicada, economia, finanças (Black and Scholes é baseado nesse conceito) e física.

Esse processo é um caso particular do processo markoviano no qual considera que a única informação necessária para determinar o estado futuro é o estado atual (não é necessário a memória do restante do processo), em que a distribuição é normal com média 0 e variância 1.

Além disso, um movimento browniano x é caracterizado pelas seguintes propriedades:

$P(x(0) = 0) = 1$;
Estacionário Para todo $0 \le s \le t, x(t) - x(s) \sim N(0, t-s)$;
Incremento independente Se o intervalo $(S_i, t_i)$ não são sobrepostos, então $x(t_i) - x(S_i)$ são independentes;
É um processo contínuo. Pode-se dizer que é um Random Walk com amostras infinitesimais;
Não é diferenciável (a prova pode ser encontrada em Choongbum Lee, MIT open course ware).

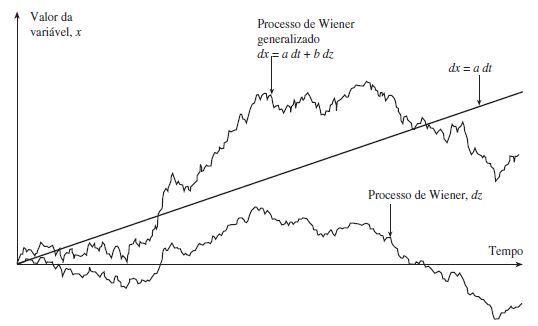
Processo de Wiener Generalizado

A generalização do processo de Wiener ocorre quando se considera que a variação não é constante em delta z. No caso do processo simples, a taxa de variância é 1 e significa que a variância da mudança em z em um intervalo de tempo delta t é igual a delta t (constante para todas as diferenças). Portanto, para incorporar no processo, denotado agora por $dz$, essa variabilidade é definida pela seguinte equação:

\[dx = adt + bdz\]

no qual $a$ e $b$ são constantes.

Para entender a equação é útil considerar os dois componentes no lado direito separadamente. O termo adt implica que $x$ tem uma taxa de derivação esperada de a por unidade de tempo. Sem o termo $bdz$ a equação é $dx=adt$ que implica que $\frac{dx}{dt}=a$. Integrando com relação ao tempo, obtemos: $x=x_0+at$, onde $x_0$ é o valor de $x$ no tempo 0. Em um período de tempo de duração $T$, a variável $x$ aumenta na quantidade $aT$. O termo $bdz$ no lado direito da equação pode ser considerado como um ruído ou variabilidade no caminho seguido por $x$. O nível desse ruído ou variabilidade é $b$ vezes um processo de Wiener. Um processo de Wiener, por sua vez, tem uma taxa de variância por unidade de tempo 1. Logo, $b$ vezes um processo de Wiener tem uma taxa de variância por unidade de tempo de $b^2$.

Lema e Cálculo de Itô

O processo de Itô acontece quando a generalização do processo de Winer assume que os termos $a$ e $b$ da equação são funções do valor do ativo (x) e do tempo (t), fornecendo a seguinte fórmula:

\[dx = a(x,t)dt + b(x,t)dz\]

A taxa de derivação e a taxa de variância esperadas de um processo de Itô podem mudar com o tempo. Em um pequeno intervalo entre t e $t + \Delta t$, a variável muda de $x$ para $x + \Delta x$, onde, $\Delta x = a(x,t)\Delta t + b(x,t)\epsilon\sqrt{\Delta t}$.

Essa equação envolve uma pequena aproximação. Ela pressupõe que a taxa de derivação e de variância de $x$ permanecem constantes, iguais a seus valores no tempo t, durante o intervalo de tempo entre $t$ e $t + \Delta t$.

O lema de Itô parte de uma expansão de Taylor para resolver o problema da não diferenciação (variação quadrática $dx^2 = dt$) do movimento Browniano para chegar em uma fórmula analítica. O lema de Itô para uma função qualquer G de x e t segue o processo:

$dG = (\frac{dG}{dx}+\frac{dG}{dt}+\frac{1}{2}\frac{d^2G}{dx^2}b^2)dt + \frac{dG}{dx}bdz$,

No qual $dz$ é o mesmo processo de Wiener que na equação. Assim, G também segue um processo de Itô, com taxa de derivação de: $\frac{dG}{dx}a+\frac{dG}{dt}+\frac{1}{2}\frac{d^2G}{dx^2}b^2)dt$. E a taxa de variância de: ${\frac{dG}{dx}}^2 b^2$.

A partir desse lema de Itô que o modelo Black and Scholes é elaborado, mostrando a relação entre preço do ativo, taxa livre de risco, volatilidade e suas gregas.

Black and Scholes

O modelo de Black and Scholes surgiu na década de 70 e até hoje é utilizado como modelo padrão para precificação de opções. Ele foi feito para opções europeias seja compra (call) europeias com tempo contratado definido (fixo) e considera que a taxa de juros livre de risco (Taxa Selic) seja constante e conhecida e o preço segue um movimento Browniano geométrico com tendência e volatilidade constantes, sua fórmula é dada por:

\[dS(t) = \mu Sdt + \sigma SdW(t)\]

No qual $S(t)$ é valor do ativo subjacente no tempo $t, \mu$ é a tendência, $\sigma$ é a volatilidade (constante) de $S$ e $dW(t)$ é processo estocástico em relação ao ativo $S$.

Portanto, é uma aplicação que possui as características de um processo de Itô.

A partir da fórmula de black and Scholes é possível chegar nas seguintes fórmulas de Call e Put para as opções:

$C(S,t) = SN(d_1) - K e^{-r(T-1)} N(d_2)$ $P(S,t) = X e^{-r(T-1)}N(-d_2) - SN(-d_1)$ $d_1 = \frac{ln(\frac{S}{K})+(r+\frac{\sigma^2}{2})(T-t)}{\sigma\sqrt{(T-t)}}$ $d_2 = d_1 - \sigma\sqrt{(T-t)}$

No qual $K$ é o preço de exercício da opção (Strike) e N(.) é a distribuição normal acumulada padronizada.

A partir da equação de Black and Scholes é possível calcular as gregas, que são as derivadas parciais em relação ao preço, volatilidade, tempo e a taxa livre de risco. A interpretabilidade de cada grega é:

Delta (derivada no preço): o quanto o preço da opção irá se alterar conforme o preço do ativo subjacente altera;
Gamma (segunda derivada no preço, aceleração): a velocidade de mudança do Delta;
Theta (derivada no tempo): sensibilidade do preço da opção conforme o tempo passa ao longo dos dias;
Vega (derivada na volatilidade): como o preço da opção se move dado o tamanho da volatilidade do ativo;
Rho (derivada na taxa livre de risco): mudanças na taxa de juros livre de risco.

Análise e simulação de dados

Para a análise foi utilizado apenas simulações de dados, uma vez que estamos estudando os processos teóricos é pertinente observar as caracteristicas mencionadas de cada um. Para estimar o valor da opção e das gregas pelo Black and Scholes foram utilizados valores arbitrários mas que representam a realidade, para expandir o uso para determinado ativo real basta substituir os valores pelos valores do próprio ativo de interesse.

O software R de computação estatística foi utilizado.

O primeiro processo simulado é a cadeia de markov. Foi criado uma matriz com 3 estados, chamados de estados 1, 2 e 3. São colocados os valores de transição entre cada zona de forma que a matriz mc_zona indica na linha os estados iniciais e as colunas os estados finais com as probabilidades de transição de um passo ao longo da matriz.

Para calcular a transição a nível de 2 passos, basta elevar a matriz ao quadrado, ou seja, sair de determinado estado e ir para outro estado em 2 movimentos. Para os demais passos basta repetir o processo.

A última matriz gerada são os valores de convergência dos estados, ou seja, no limite (depois de muito tempo) qual a probabilidade de estar em cada estado independente do estado de partida. Assim, pelo exemplo o primeiro estado é o mais provável com 38,8% e o terceiro o menos provável com 27,7%.

# cadeias de markov
library(markovchain)

zona <- c("1","2","3")
zona_transicao <- matrix(c(0.3,0.3,0.4,0.4,0.4,0.2,0.5,0.3,0.2),nrow = 3, byrow = T)
dimnames(zona_transicao) <- list(zona,zona)
zona_transicao

mc_zona <- new('markovchain',
               transitionMatrix = zona_transicao, # These are the transition probabilities of a random industry
               states = zona, byrow=T)

# Matriz de transição em 1 passo
mc_zona

# 2 passos
mc_zona^2

# Convergência dos estados, estado inicial não interessa mais
steadyStates(mc_zona)

Para simular o random walk, foi gerado a partir da simulação do modelo ARIMA (um modelo famoso que possui componentes autorregressivas e de médias moveis) com 0 componentes autorregressivas e 0 componentes de médias móveis (parâmetros no order), ou seja, é um ARIMA apenas com o termo aleatório. Ao simular o processo, verificamos o caminhar aleatório do processo para valores negativos mas sempre com movimentos de alta para se aproximar de zero, cada observação é um novo ruído branco. Além disso, ao observarmos a primeira observação parte do valor 0, indicando que está centralizado o processo. Portanto, é um passeio aleatório.

# Passeio aleátorio

# sem média e variância especificados
# forte dependência no tempo
# incrementos são ruído branco

set.seed(10)
rw <- arima.sim(model=list(order=c(0,1,0)),n=500)
head(rw)
ts.plot(rw, main="Random Walk (Passeio aleatório)")

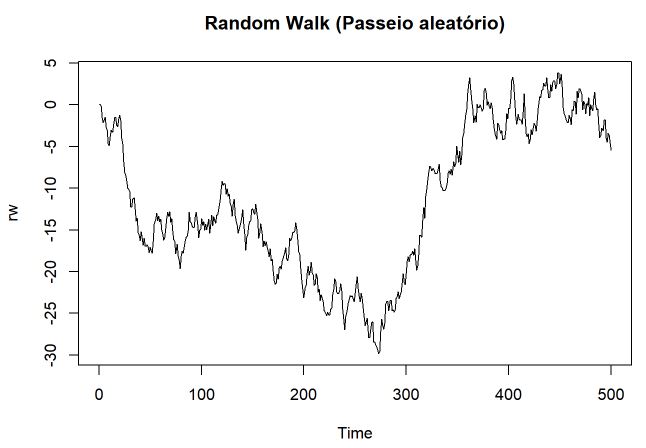
Para simular o movimento browniano foi gerado a partir da distribuição normal padrão (N(0,1)) 10.000 observações e somado seus valores ao longo do processo.

Novamente é observado o caminho aleatório do processo alternando entre valores positivos e negativos. Portanto, pelo gráfico verifica-se que é estacionário e como cada observação foi gerado de uma normal de forma independente, seus incrementos são independentes. Pelo gráfico, verificasse maior granularidade do que Random Walk (amostras infinitesimais).

# Movimento Browniano
set.seed(10)
dis = rnorm(10000, 0, 1); # Normal!
dis = cumsum(dis);
plot(dis, type= "l",main= "Movimento Browniano", xlab="Tempo", ylab="Valor")

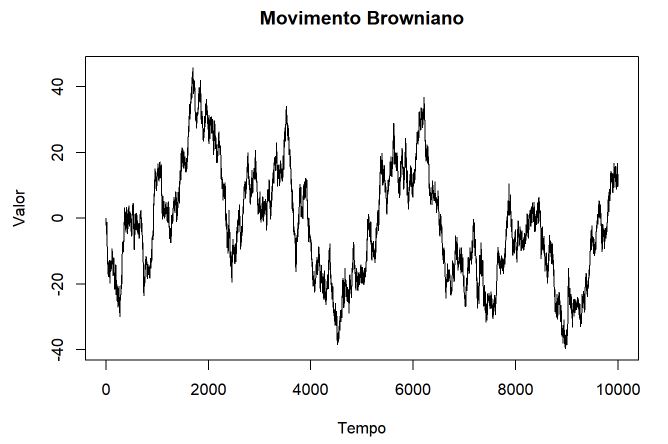
É possível fazer o mesmo processo utilizando o comando rwiener que gera valores aleatórios do processo. Dessa forma, segue novamente o processo mas com um código alternativo.

# Movimento Wiener
library(e1071)
set.seed(10)
wiener <- rwiener(end = 1, frequency = 1000)
# end =	tempo da última observação
# frequency =	número de observações por unidade de tempo.
# Exatamente por ser tempo contínuo é declarado o intervalo final

plot(wiener,type="l",main= "Movimento Wiener", xlab="Tempo", ylab="Valor")

Para finalizar, será calculado o preço de uma opção e de sua grega pelo Black and Scholes que resume tudo o que foi abordado nesse post, o uso desses processos em finanças é muito grande mas não se resume a essa área.

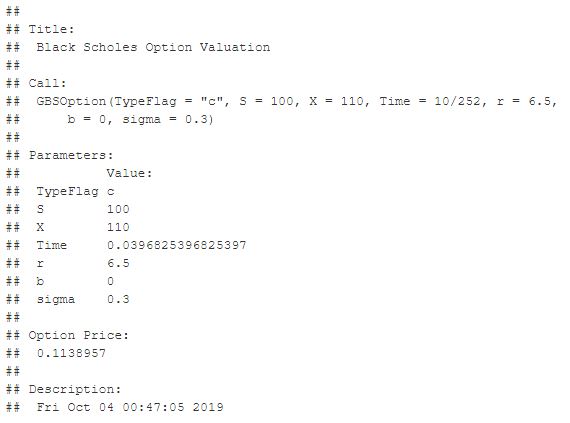
Para calcular o preço de determinada opção de um ativo qualquer, pode ser usado o comando GBSOption, no qual é necessário informar se é uma opção de compra (‘c’) ou venda (‘p’), o valor do ativo no momento (S), o valor do strike (‘X’), o tempo para expirar em anos a opção (‘Time’), a taxa livre de risco (‘r’), a taxa de dividendos paga (‘b’) e a volatilidade do ativo (‘sigma’).

Nesse exemplo, foram passados valores próximos aos de mercado mas sem nenhum ativo em particular, para utilizar a mesma função para um ativo como PETR4 basta mudar os valores para os valores do ativo.

Dessa forma, a função retorna o valor de compra segundo Black and Scholes, para esses valores de input o valor é R$0,11, ou seja, a partir disso pode-se verificar se o mercado está precificando a opção conforme Black and Scholes ou se está sobreprecificando ou subprecificando, podendo ser o início de uma estratégia.

# Black and Scholes

library(fOptions)

GBSOption(TypeFlag = "c", S = 100, X = 110, 
          Time = 10/252, r = 6.5,
          b = 0, sigma = 0.3)

Da mesma forma que a função anterior calculava o preço da opção, a função GBSGreeks calcula as gregas de Black and Scholes. Além dos parâmetros já informados anteriormente, é necessário dizer qual grega é de interesse podendo ser o “delta”, “gamma”, “vega”, “theta” ou “rho”.

Nesse exemplo, ao calcularmos a grega delta obtemos o valor de 0,04, ou seja, a probabilidade de exercício dessa opção com essas características é de apenas 4%.

GBSGreeks(Selection = "delta", TypeFlag = "c", S = 100, 
                 X = 110,
                 Time = 10/252, r = 6.5, b = 0, 
                 sigma = 0.3)

Referências

Elementary Stochastic Calculus with Finance in View. Mikosch, Thomas. University of Copenhagen. World Scientific Publishing.

John C Hull.Opções, futuros e outros derivativos. Bookman, 9oedition, 2016.Tradução: Francisco Araújo da Costa ; revisão técnica: Guilherme Ribeiro de Macêdo.

Apresentação Opções reais. Prof. Luiz Brandão, IAG PUC-Rio, brandao@iag.puc-rio.br

MIT open course ware. Choongbum Lee. Lectures 5,17,18. https://ocw.mit.edu/courses/mathematics/18-s096-topics-in-mathematics-with-applications-in-finance-fall-2013/video-lectures/