O Método dos Mínimos Quadrados Ordinários e Regressão Linear Simples

1. Introdução: o que é a Econometria?

A econometria é um campo de estudo baseado no desenvolvimento de métodos e ferramentas estatísticos para aplicação em dados econômicos. Pode ser usada para testar teorias, avaliar planos e auxiliar na tomada de decisões.

Um modelo econométrico pode ser desenvolvido a partir de um modelo econômico formal, mas também pode ser baseado em raciocínios econômicos informais e na prórpria intuição.

Um exemplo de aplicação da econometria é o estudo dos determinantes do salário. Podemos deduzir que a função que determina o salário é composta de diversos argumentos, cada qual representante de um fator observável: nível de educação, experiência prévia, qualidade da educação, aptidão inata, entre outros. Ao montarmos um modelo econométrico de forma a estudar como estes fatores influenciam na determinação do salário, estimamos parâmetros \(\beta\) que descrevem as direções e as influências da relação entre a variável salário e os fatores usados para determiná-lo.

Onde:

• salário é o indicador medindo o nível salarial
• educ é a variável que mede o número de anos de educação formal
• exper é a variável que mede o número de anos de experiência de trabalho
• u é o termo contém todos os fatores não observados, como a aptidão; é denominado termo de erro

O objetivo da análise econométrica é estimar os parâmetros do modelo e testar hipóteses sobre esses parâmetros; os valores e os sinais dos parâmetros podem determinar a validade (ou não) de uma teoria econômica, assim como os efeitos de determinadas políticas e decisões.

Quando da realização de hipóteses nas ciências sociais, as noções de ceteris paribus e de inferência causal são de grande importância. A primeira se referere a que, ao se estudar a relação entre duas variáveis, todos os outros fatores relevantes devem permanecer fixos. Além disso, descobrir relações causais é uma difícil tarefa, em razão da natureza não experimental (isto é, não controlável) dos dados coletados.

2. Modelo de regressão simples

2.1 Definição de um modelo de regressão simples

Um modelo de regressão simples estuda a relação entre duas variáveis quaisquer. Iremos chamar a variável y de variável dependente, e x de variável independente. Assim, estaremos estabelecendo que nosso intuito é observar como \(y\) varia a partir de variações em \(x\). Já um modelo de regressão múltipla constitui uma extensão do modelo simples na medida em que permite a inclusão de mais variáveis independentes no modelo de interesse; para este post, no entanto, estaremos nos limitando à análise de uma regressão linear simples.

Podemos escrever uma equação que relaciona y e x da seguinte forma:

Onde o termo de erro u agrega todos os fatores não observados na equação que podem influenciar o valor de \(y\). Temos ainda \(\beta_0\), que é o parâmetro de intercepto da equação (ou uma constante) e \(\beta_1\) que é o parâmetro de inclinação da relação entre \(y\) e \(x\), mantidos fixos os outros fatores em \(u\).

A equação (1) trata da relação entre \(y\) e \(x\). Se os fatores contidos em no termo de erro são mantidos fixos, de modo que \(\Delta u=0\), então \(x\) terá um efeito linear sobre \(y\), de modo que a variação em \(y\) é o coeficiente \(\beta_1\) multiplicado pela variação em \(x\):

2.2 Derivação das estimativas de mínimos quadrados ordinários

Agora iremos tratar da estimação dos parâmetros \(\beta_0\) e \(\beta_1\) da equação (1). Para tanto, faz-se necessário obter uma amostra da população; considere {(\(x_i\), \(y_i\)): i = 1, …, \(n\)} como sendo uma amostra aleatória de tamanho \(n\) da população. Podemos escrever \(y_i=\beta_0+\beta_1 x_i+u_i\), onde \(u_i\) é o termo de erro para cada observação i.

Faremos uso da seguinte hipótese: na população, u tem média zero e não é correlacionado a x. Assim, u tem média zero (equação 2) e a covariância entre x e u é zero (equação 3).

e

Reescrevnedo em termos das variáveis observáveis y e x e dos parâmetros desconhecidos \(\beta_0\) e \(\beta_1\):

e

As equações (4) e (5) podem ser usadas para estimar os parâmetros desconhecidos de modo a obter bons estimadores \(\hat{\beta_0}\) e \(\hat{\beta_1}\). De fato, para uma dada amostra de dados, escolhemos as estimativas \(\hat{\beta_0}\) e \(\hat{\beta_1}\) para resolver as equivalências amostrais de (4) e (5):

e

Podemos ainda reescrever a equação (6) como

o que nos dá

Ou seja, quando obtemos uma estimativa do parâmetro de inclinação \(\hat{\beta_1}\), obtemos também uma estimativa do intercepto, dados os valores médios \(\overline{y}\) e \(\overline{x}\).

Suprimindo \(n^{-1}\) de (7) e inserindo (9) na equação, obtemos: \(\sum_{i=1}^{n} x_i(y_i-(\overline{y}-\hat{\beta_1}\overline{x})-\hat{\beta_1}x_i)=0\) a qual pode ser, por sua vez, reescrita como \(\sum_{i=1}^{n} x_i(y_i-\overline{y})=\hat{\beta_1}\sum_{i=1}^{n}(x_i-\overline{x})\)

Das propriedades do operados somatório, observe que: \(\sum_{i=1}^{n} x_i(x_i-\overline{x}) = \sum_{i=1}^{n} (x_i-\overline{x})^{2}\qquad e \qquad\sum_{i=1}^{n} x_i(y_i-\overline{y}) = \sum_{i=1}^{n} (x_i-\overline{x})(y_i-\overline{y})\)

O que nos informa que a inclinação estimada deve ser

A equação (10) nada mais é do que a covariância amostral entre \(x_i\) e \(y_i\) dividida pela variância amostral de \(x_i\). Assim, podemos escrever \(\hat{\beta_1}\) como:

Em que \(\hat{\rho}_{x_y}\) é a correlação amostral entre \(x_i\) e \(y_i\), e \(\hat{\sigma}_x\) e \(\hat{\sigma}_y\) denotam os desvios padrão da amostra. Disto temos a implicação de que se \(x_i\) e \(y_i\) forem positivamente correlacionados na amostra, \(\hat{\beta_1}<0\) (o contrário também é válido).

As estimativas dadas por (9) e (10) são denominadas de estimativas de mínimos quadrados ordinários (MQO) de \(\beta_0\) e \(\beta_1\).

Seja \(\hat{y_i}\) um valor estimado de y quando \(x\) = \(x_i\), de tal forma que obtemos \(\hat{y_i}=\hat{\beta_0}+\hat{\beta_1}x_i\). O resíduo da observação i é a diferença entre o valor verdadeiro de \(y_i\) e seu valor estimado:

É importante observar que os resíduos não são iguais ao termo de erro. Agora, suponha que escolhamos \(\hat{\beta_0}\) e \(\hat{\beta_1}\) com a finalidade de fazer a soma dos quadrados dos resíduos,

tão pequena quanto possível. O nome “mínimos quadrados ordinários” vem do fato de que as estimativas (9) e (10) minimizam essa soma dos quadrados dos resíduos dada em (13).

Há três propriedades dos estimadores de MQO muito importantes para análise econmétrica. A primeira delas é de a soma, e portanto a média amostral dos resíduos de MQO é zero:

As estimativas de MQO \(\hat{\beta}_0\) e \(\hat{\beta}_1\) são escolhidas para que esse resultado seja válido. A segunda é de que a covariância amostral entre os regressores e os resíduos de MQO é zero. Já a terceira é de que o ponto (\(\overline{x}, \overline{y}\)) sempre está sobre a reta de regressão de MQO.

2.3 Minimizando a soma dos quadrados dos resíduos

Iremos agora expandir o resultado da última subseção, de modo a providenciar amparo à noção de que \(\hat{\beta}_0\) e \(\hat{\beta}_1\) são os estimadores que minimizam a soma dos quadrados dos resíduos. Formalmente, o problema é caracterizar as soluções \(\hat{\beta}_0\) e \(\hat{\beta}_1\) para o problema de minimização:

onde \(b_0\) e \(b_1\) são argumentos dummy para o problema de otimização.A condição necessária para \(\hat{\beta}_0\) e \(\hat{\beta}_1\) resolver o problema é que as derivadas parciais de Q(\(b_0\),\(b_1\)) em relação a \(b_0\) e \(b_1\) devem ser zero quando estimadas com \(\hat{\beta}_0\) e \(\hat{\beta}_1\):

e

Repare que essas duas equações são exatamente iguais a (6) e (7) multiplicadas por \(-2n\) e, portanto, são solucionadas por \(\hat{\beta}_0\) e \(\hat{\beta}_1\).

Uma forma de verificar que minimizamos a soma dos quadrados dos resíduos é escrever, para qualquer \(b_0\) e \(b_1\),

Agora usamos as propriedades dos estimadores de MQO, a que chegamos a:

Visto que essa expressão é uma soma de termos quadráticos, o seu menor valor possível é zero. Logo, esse valor ocorre quando \(b_0\)=\(\hat{\beta}_0\) e \(b_1\)=\(\hat{\beta}_1\).

2.4 Características de MQO em uma amostra de dados

Da primeira propriedade de MQO introduzida na subção 2.2, tem-se que a média dos resíduos é zero; equivalentemente, a média amostral dos valores estimador, \(\hat{y}_i\), é a mesma da média amostral de \(y_i\), ou \(\overline{\hat{y}} = \overline{y}\). Além disso, as duas primeiras propriedades podem ser usadas para mostrar que a covariância amostral entre \(\hat{y}_i\) e \(\hat{y}_i\) é zero. Podemos ver o método dos quadrados ordinários como um processo que decompõe \(y_i\) em duas partes: um valor ajustado e um resíduo.

Defina a soma dos quadrados total (SQT), a soma dos quadrados explicada (SQE) e a soma dos quadrados dos resíduos (SQR) como a seguir:

As equações acima são medidas de variação amostral. A variação total em \(y_i\) pode ser expressa como a soma da variação explicada e da variação não explicada.

O R-quadrado da regressão é definido como

O \(R^{2}\) é a razão entre a variação explicada e a variação total; assim, ele é interpretado com a fração da variação amostra em \(y\) que é explicada por \(x\). É um número que mede quão bem a reta de regressão de MQO se ajusta aos dados.

O valor de \(R^{2}\) está sempre contido entre zero e um; um valor de \(R^{2}\) quase igual a zero indica um ajuste ruim da reta de MQO.

2.5 Valores esperados e variâncias dos estimadores de MQO

2.5.1 Inexistência de viés em MQO

Para estabelecer a inexistência de viés do método dos mínimos quadrados ordinários, faz-se necessário lançar mão de algumas hipóteses. Importante notar que as seguintes hipóteses, denotadas por RLS.#, são aplicadas ao caso da regressão linear simples.

A primeira hipótese (RLS.1) define o modelo populacional; nele, a variável dependente está relacionada à variàvel independente \(x\) e ao erro \(u\) da seguinte forma:

em que \(\beta_0\) e \(\beta_1\) são os parâmetros de intercepto e de inclinação populacionais, respectivamente.

A segunda hipótese (RLS.2) é de que podemos usar uma amostra aleatória de tamanho \(n\), {(\(x_i\), \(y_i\)): i = 1, 2, …, \(n\)}, proveniente de um modelo populacional. Estamos interessados em usar os dados de \(y\) e \(x\) para estimar os parâmetros beta.

Podemos escrever (22) em termos da amostra aleatória como

A terceira hipótese (RLS.3) é de os resultados amostrais em \(x\), ou seja, (\(x_i\), i = 1, 2, …, \(n\)) não são todos de mesmo valor.

A quarta hipótese (RLS.4) é a de que o erro \(u\) tem um valor esperado igual a zero, dado qualquer valor da variável esxplicativa: \(E(u \vert x) = 0\).

Agora, da equação (10), temos

Sendo a variação total em \(x_i\) igual a \(SQT_x\), e substituindo (23) em (24):

Por meio de álgebra, podemos escrever o numerador de \(\hat{\beta_1}\) como

Sabendo que \(\sum_{i = 1}^{n} \, (x_i - \overline{x}) = 0\) e \(\sum_{i = 1}^{n} \, (x_i - \overline{x})x_i = \sum_{i = 1}^{n} \, (x_i - \overline{x})^{2} = SQT_x\), temos que a expressão resulta em

Assim, o estimador \(\hat{\beta}_1\) é igual à inclinação populacional \(\beta_1\) somada a um termo que é a combinação linear dos erros. A diferença entre \(\hat{\beta}_1\) e \(\beta_1\) se dá pelo fato de que esses erros são, em geral, não-nulos.

Usando as hipóteses RLS.1 a RLS.4, podemos afirmar que

em outras palavras, \(\hat{\beta}_0\) é não viesado para \(\beta_0\) e \(\hat{\beta}_1\) é não viesado para \(\beta_1\).

2.5.2 Variâncias dos estimadores de MQO

A variância dos estimadores de MQO pode ser calculada sob as hipóteses RLS.1 a RLS.4. Em razão da complexidade da expressão dessas variâncias, vamos adicionar uma hipótese conhecida com a hipótese de homoscedasticidade (RLS.5): o erro u tem a mesma variância, dado qualquer valor da variável explicativa:

É útil escrever RLS.4 e RLS.5 em termos de média condicional e da variância condicional de y:

\(E(y|x) = \beta_0 + \beta_1x \tag{30}\) \(Var(y|x) = \sigma^{2} \tag{31}\)

Agora, sob as hipóteses RLS.1 a RLS.5,

e

De (33), atesta-se que quanto maior a variância do erro, maior é Var(\(\hat{\beta}_1\)), já que uma variação maior nos fatores não observáveis que afetam \(y\) faz com que seja mais difícil estimar com precisão o parâmetro. Por outro lado, uma maior variabilidade na variável independente é preferível, pois será mais fácil descrever a relação entre \(E(y \vert x)\) e \(x\).

2.5.3 Estimação da variância do erro

As fórmulas (32) e (33) permitem-nos isolar os fatores que contribuem para Var(\(\hat{\beta}_1\)) e Var(\(\hat{\beta}_0\)). No entanto, essas fórmulas são em geral desconhecidas. Podemos, contudo, usar os dados para estimar \(\sigma^{2}\).

Primeiro, \(\sigma^{2} = E(u^{2})\), de modo que um “estimador” não viesado de \(\sigma^{2}\) é \(n^{-1}\sum_{i = 1}^{n} \, u_{i}^{2}\). Entretanto esse “estimador” não atende às nossas necessidades, já que os erros não são observados. Temos, contudo, os resíduos \(\hat{u}_i\) de MQO. Se substituímos os erros pelos resíduos de MQO, obtemos \(SQR/n\).

Esse sim é um esimador verdadeiro, ainda que viesado, porque ele não explica a razão de duas restrições que devem ser satisfeitas pelos resíduos de MQO: \(\sum_{i = 1}^{n} \, \hat{u}_i = 0\) e \(\sum_{i = 1}^{n} \, x_i\hat{u}_i = 0\). De forma a observar essas restrições é assumir n-2 graus de liberdade nos resíduos de MQO. O estimador não viesado de \(\sigma^{2}\) que faz um ajustamento aos graus de liberdade é:

O estimado dos desvios padrão de \(\hat{\beta}_1\) e \(\hat{\beta}_0\) é

e é chamado erro padrão da regressão (EPR).

Como dp(\(\hat{\beta}_1\)) = \(\sigma / \sqrt{SQT_x}\), o estimador natural de dp(\(\hat{\beta}_1\)) é:

que é chamado de erro padrão de $\hat{\beta}_1$. Semelhantemente, ep(\(\hat{\beta}_0\)) é obtido de dp(\(\hat{\beta}_0\)) ao substituir \(\sigma\) por \(\hat{\sigma}\). O erro padrão de qualquer estimativa nos dá uma ideia de quão preciso é o estimador.

3. Exemplo de regressão linear

Como exemplo de aplicação de regressão linear, queremos relacionar notas de testes com a proporção de estudantes por professor obtidos de uma base de dados referentes a escolas da Califórnia (EUA). A nota dos testes (TestScore) é a média das notas de leitura e matemática para classes do 5º ano; já o tamanho das salas é medido pela proporção de estudantes relativa à quantidade de professores (que a partir deste ponto será identificada como STR, ou student-teacher ratio). Os dados são provenientes do banco de dados CASchools, contido no pacote AER disponível para R.

library(AER)
data(CASchools)

É importante notar que as duas variáveis de interesse não estão incluídas no pacote: faz-se necessário computá-las manualmente a partir dos dados contidos em CASchools.

# Compute STR e TestScore e junte-os a CASchools
CASchools$STR <- CASchools$students/CASchools$teachers
CASchools$score <- (CASchools$read + CASchools$math)/2

De modo a estimar o modelo por MQO, definindo TestScore como a variável dependente e STR como a variável independente, fazemos uso da função lm() do R para realizar uma regressão linear simples.

# Estimando o modelo
linearmodel <- lm(score ~ STR, data = CASchools)
# Descobrimos os parametros beta estimados pelo modelo:
linearmodel

##Call:
##lm(formula = score ~ STR, data = CASchools)
##
##Coefficients:
##(Intercept)          STR  
##     698.93        -2.28 

Agora, plotamos os dados e o modelo estimado em um gráfico.

# Plotando os dados
plot(score ~ STR,
    data = CASchools,
    main = "Grafico de dispersao de TestScore e STR",
    xlab = "STR (X)",
    ylab = "Test Score (Y)",
    xlim = c(10, 30),
    ylim = c(600, 720))
# Adicionando a linha de regressao estimada
abline(linearmodel)
\end{lstlisting}

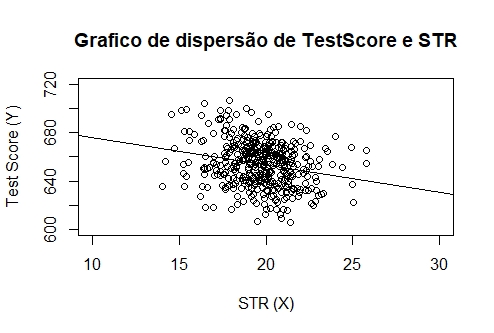
A interpretação do modelo é simples: a relação entre TestScore e STR é negativa, ou seja, escolas onde se observa uma maior proporção de estudantes relativa à quantidade de professores apresentam notas menores em testes. Pelo modelo estimado, há uma queda de aproximadamente 2.3 pontos na nota dos testes para um aumento observado no STR de um aluno por professor.

Para identificar o \(R^{2}\) e o erro padrão da regressão (EPR), aplicamos o comando summary().

summary(linearmodel)


##Call:
##lm(formula = score ~ STR, data = CASchools)

##Residuals:
##    Min      1Q  Median      3Q     Max 
##-47.727 -14.251   0.483  12.822  48.540 

##Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
##(Intercept) 698.9329     9.4675  73.825  < 2e-16 ***
##STR          -2.2798     0.4798  -4.751 2.78e-06 ***
---
##Signif. codes:  
##0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

##Residual standard error: 18.58 on 418 degrees of freedom
##Multiple R-squared:  0.05124,	Adjusted R-squared:  0.04897 
##F-statistic: 22.58 on 1 and 418 DF,  p-value: 2.783e-06

O \(R^{2}\) deste modelo tem um valor de 0,051. Logo, 5,1% da variação da variável dependente TestScore é explicada pela variável independente STR, ou seja, a regressão explica pouco da variação nas notas, e muito dessa variação permanece inexplicada. O erro padrão da regressão, por sua vez, é de 18,58; isso indica que na média o desvio da nota realmente obtida em relação à reta de regressão é de 18,58 pontos.

Referências:

BUSAB, W. MORETTIN, P. Estatística Básica: 9ª Edição. São Paulo, SP: Saraivauni, 2017.

HANCK, Cristoph. et al. Introduction to Econometrics with R. Disponível em: https://www.econometrics-with-r.org/.

KUTNER, Michael H. et al. Applied linear statistical models: 5th ed. McGraw-Hill/Irwin, 2004.

PAULA, Gilberto A. Modelos de regressão com apoio computacional. São Paulo, SP: Instituto de Matemática e Estatística, Universidade de São Paulo. 2013.

PINDYCK, R. RUBINFELD, D. Econometric models and economic forecasts. McGraw-Hill/Irwin, 1998.

STOCK, J; WATSON, M. Introduction to econometrics: 3rd ed. Pearson, 2010.

WOOLDRIDGE, Jeffrey M. Introdução à econometria: uma abordagem moderna: tradução da 6ª edição norte-americana. São Paulo, SP: Cengage Learning, 2016.

• ← Previous Post
• Next Post →