Markowitz - Seleção de carteiras

Definição de risco e retorno

Considere uma série de preços de uma ação em que cada preço de refere a uma observação em um determinado período de tempo:

O retorno efetivo do ativo no período \(t=2\) é dado por \(R_{2} = p_{2} - p_{1}\). A ideia é que se um agente comprasse o ativo no período 1 ao preço \(p_1\) e o vendesse no período 2 ao \(p_2\), ele teria o ganho de \(R_2\) unidades monetárias. Entretanto, para que essa medida de ganho seja comparável entre ativos diferentes se usa frequentemente o retorno percentual como medida de retorno, isto é:

Os valores de retornos efetivos já observados são chamados também de retornos históricos.

Uma medida mais interessante para o investidor é qual será o retorno do ativo no futuro. Este tipo de retorno é chamado de retorno esperado. Enquanto o retorno efetivo diz respeito ao que ocorreu de fato, o retorno esperado desrespeita ao que ocorrerá no futuro, portanto, uma expectativa. Matematicamente, pode-se definir o retorno esperado como:

Em outros termos, o retorno esperado é o somatório dos retornos do ativo ponderado pelo pelas respectivas probabilidades de ocorrência. Assim, para calcular o retorno esperado pela definição deve-se saber todos os retornos que o ativo pode ter e quais as probabilidades associados a eles. Isso significa dizer que se conhece todos os cenários que podem ocorrer, suas probabilidades e retornos associados a eles.

Na maioria dos casos, não se tem este tipo de conhecimento sobre os retornos de determinado ativo. Nesse caso, os retornos históricos podem serem usados para estimar o retorno esperado, mas não há nenhuma garantia de que o retorno futuro será o mesmo que o já observado no passado. Disto isto, neste post o retorno esperado de um ativo será estimado como sendo a média aritmética do retornos históricos. Essa abordagem será adotada em razão da sua simplicidade.

Além da medida de retorno, outra medida de grande importância para os investidores é o risco associado aos ativos. Tal métrica mede o quanto em média o valor do retorno efetivo irá divergir do retorno esperado. Isso significa que ativos com risco alto têm retornos efetivos que divergem bastante do retorno esperado, ao mesmo tempo que o ativos menos arriscados têm retornos efetivos que divergem pouco do retorno esperado.

O gráfico a seguir ilustra intuitivamente essa ideia. Considere dois ativos que têm o retorno esperado de 4%, entretanto o ativo A possui um risco menor que o ativo B:

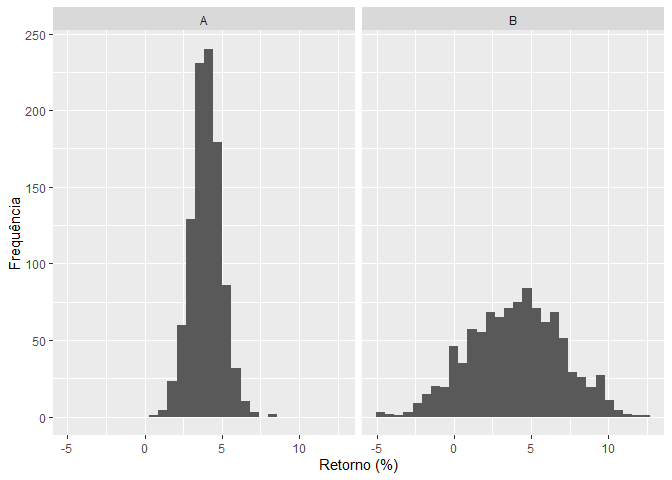
Como consequência os retornos efetivos do ativo A são bem mais concentrados, ou próximos, ao retorno esperado do ativo. Ao mesmo tempo que os retornos efetivos de ativo B são bem mais dispersos. Formalmente, o risco de um ativo é definido como o desvio padrão dos retornos efetivos em relação ao retorno esperado:

O desvio padrão não é a única medida para avaliar risco. A semi-variância ou downside risk é outro exemplo de medida de risco. Ela formula a ideia de que a variância oriunda de retornos efetivos acima do retorno esperado não deveria ser computado como risco. Pois, quando o retorno efetivo for maior que o retorno esperado isso é um risco “bom”, porém, o risco é em geral associado ao custo de manter determinado ativo.

Nesse post será usado o desvio padrão como medida de risco. Além disso, cabe considerar que a discussão sobre a viabilidade de calcular o retorno a partir da definição se aplica também para o cálculo do risco. Dessa forma, será usado o desvio padrão histórico como estimador para o risco.

Risco e retorno para carteiras

Até agora foi abordado o risco e retorno do ponto de vista de um ativo individual. Entretanto, seria interessante analisar vários ativos em conjunto. Essa é a ideia de carteira. De modo geral, uma carteira é um conjunto de ativos, a participação de cada ativo no valor total da carteira é chamado de peso do ativo na carteira. Assim, se um ativo alcança o valor $ 10 em uma carteira com o valor total de $ 100, então esse ativo tem peso de 10% na carteira.

Dito isso, o retorno esperado de uma carteira é dada por:

Em que \(n\) é a quantidade de ativos que compõe a carteira, \(w_i\) a participação de do ativo \(i\) na carteira e \(R_i\) o retorno esperado do ativo \(i\). Usando a notação matricial podemos descrever essa relação como um produto interno entre dois vetores:

Sendo \(w\) um vetor coluna com as participações dos ativos na carteira e \(w'\) a sua transporta e \(R\) outro vetor coluna que contém os retornos dos ativos da carteira:

De agora em diante, um vetor sempre será tratado como uma matriz com uma coluna.

Já o variância da carteira - quadrado do seu risco - é definida como:

Para o caso de uma carteira com dois ativo podemos reescrever a relação como:

Sendo \(cov(R_i,R_i) = var(R_i) = \sigma_{ii} = \sigma_{i}^2\) e \(cov(R_i, R_j) = cov(R_j, R_i)\) segue:

Diferente do caso do retorno, o risco de uma carteira não é igual à média ponderada dos riscos de cada ativo. A razão para isso é que em geral sempre há uma relação entre a evolução de um preço de ativo \(A\) e um ativo \(B\), por exemplo, há um relação entre a evolução dos preços das ações da Petrobras e da Vale dado que ambas exportam commodities. No caso da carteira com dois ativos, o relacionamentos entre os dois ativos é captado pela covariância entre eles, \(\sigma_{12}\).

O risco de uma carteira com n ativos pode ser definido como:

\(Var(R_p) = w'\Omega w\) Novamente \(w\) é o vetor com a participação de cada ativo na carteira, já \(\Omega\) é a matriz do covariância dos retornos dos ativos:

Assim, cada célula \(\sigma_{ij}\) da matriz é a covariância entre os retornos do ativo \(i\) e dos retornos do ativo \(j\). Como \(\sigma_{ij} = \sigma_{ji}\), \(\Omega\) é uma matriz simétrica cuja diagonal é a variância dos ativos.

Tipos de Risco

O risco, pode ser dividido em dois tipos: idiossincrático, também conhecido como risco não sistemático, e sistemático.

O risco idiossincrático está associado a variância específica do ativo mensurado, é uma característica única do ativo. No caso, por exemplo, de um seguro para casas, assaltos são riscos idiossincráticos, pois dependendo da vizinhança, segurança interna ou até mesmo da aparência, cada casa possui uma chance de ser assaltada ou não, e, não necessariamente, caso uma casa seja assaltada as outras serão também. Esse risco não será tão relevante para o modelo apresentado mais a frente, isso ficará mais claro a seguir.

Já o risco sistemático é aquele ao qual estão sujeitos todos os ativos negociados, isso pode incluir não só ativos que estão listados em bolsas, como também os negociados em mercados de balcão, moedas, etc. Voltando ao exemplo do seguro, o risco sistemático seria a chance de haver um desastre natural que atingisse todas as casas, independentemente de qualquer característica individual de cada casa.

Diversificação

Para entender a diversificação é preciso que esteja clara a distinção entre os tipos de risco. O risco não sistemático então é aquele que afetará somente um ou alguns ativos. No caso das ações de uma empresa seu risco específico está relacionado às decisões de investimentos tomadas pelo gestor, investimentos com \(VPL\) positivo impactam positivamente o valor de uma ação, porém a ocorrência de greves ou fraudes terá impacto negativo.

Já como risco sistemático podemos citar eventos macroeconômicos como a inflação que afeta oferta e demanda de todo um país, é em diferentes níveis para cada tipo de bem, serviço ou setor, mas de maneira geral toda a economia é afetada.

Dadas tais diferenças é possível perceber que em uma carteira com vários ativos, apesar de todos estarem sujeitos ao risco sistemático, cada um deles terá também seu risco específico e enquanto alguns sofrem valorização outros terão queda no preço, e assim é feita a compensação de ganhos e perdas, por isso é importante que uma carteira possua um bom número de ativos e que estes sejam escolhidos de maneira que os riscos não sistemáticos tenham pouca relação entre si.

Podemos voltar então ao exemplo de uma companhia de seguros para exemplificar como funciona a diversificação. Digamos que existem apenas dois riscos envolvendo as casas asseguradas de uma cidade: desastres naturais e roubos. Não é possível a seguradora evitar que ocorram desastres ou que as casas não sejam atingidas por eles, esse risco também pode ser maior ou menor dependendo da época do ano. Porém, os roubos não atingem todas as casas ao mesmo tempo e as ocorrências podem ser maiores a depender de bairro, aparência das casas, etc. Nesse caso, seria prudente que a seguradora tivesse imóveis assegurados dos mais diferentes tipos e também em lugares diferentes. O risco de desastres não é eliminado por diversificação, porém o risco de perdas devido a assaltos diminui quanto maior for a diversificação.

Assim, o efeito diversificação consiste em na redução do risco de uma carteira numa proporção maior que a redução da média ponderada dos retornos quando se adiciona ativos na carteira.

A correlação é a medida da estatística utilizada para medir se dois ativos possuem flutuações muito ou pouco parecidas, é, no cálculo, o que fará o risco aumentar ou diminuir ao montar uma carteira de investimentos. Pode variar de -1, que é quando os ativos possuem correlação perfeitamente negativa, a 1, ativos com correlação perfeitamente positiva. Quanto mais próxima de 1, maior o risco da carteira, pois neste caso, os ativos se comportam de maneira muito parecida, e quanto mais próxima de -1, menor o desvio padrão da carteira. Entretanto, a correlação não capta relações não-lineares entre variáveis.

A correlação entre ativos pode contribuir para aumentar ou reduzir o efeito diversificação em uma carteira. Considere uma carteira com duas ações, o risco da carteira depende da correlação entre os ativos. No caso em que a correlação entre os ativos é \(-1\) o risco da carteira pode ser nulo dependendo dos pesos entre os ativos. Por outro lado, caso a correlação seja \(1\) não há efeito diversificação.

Isso é ilustrado no gráfico a seguir, em que cada ponto corresponde a um ativo:

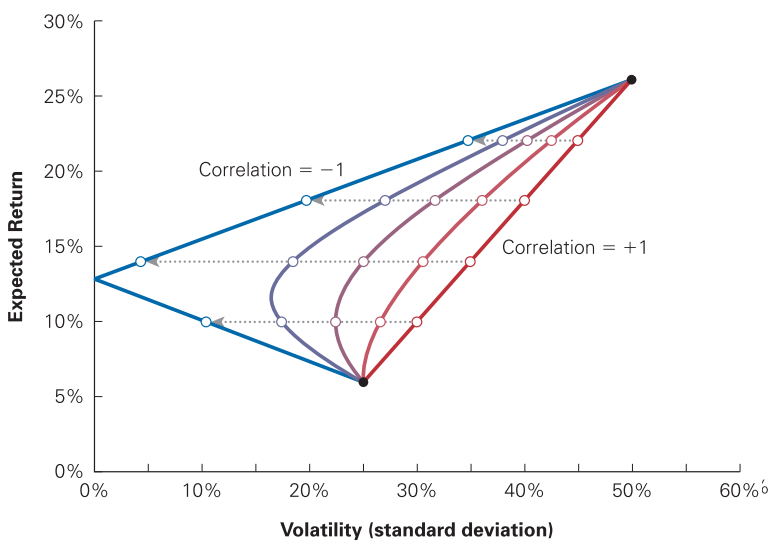
Fonte: Adaptado de BERK, 2014

Entretanto, em uma carteira com muito ativos o efeito ilustrado acima é difícil de acontecer, em razão das correlações entre os vários ativos. Nesta situação, no pior dos casos, diversificar torna o risco da carteira igual ao valor do risco sistemático dos ativos, eliminando o risco idiossincrático.

Considere um carteira com \(n\) ativos, tal que todos os ativos têm o mesmo peso na carteira. Como já mencionado, a variância de uma carteira \(p\) com \(n\) ativos é dada por:

Separando em variâncias e covariâncias segue:

Considerando que \(w_i = w_j = \frac{1}{n}\), segue:

Note que na equação acima há \(n\) variâncias, uma para cada ativo, e \(n*n - n\) covariâncias, todas as covariâncias descontadas as variâncias. Assim, a equação acima pode ser reescrita como:

Tal que:

• \(\bar{\sigma_i}^2 \equiv \frac{1}{n} \sum_i^{n}Var(R_i)\), que é a média das variâncias individuais dos ativos;
• \(\bar{\sigma_{ij}} \equiv \frac{1}{n^2-n}\sum_{\substack{ i, \ j \\i \neq j}}^{n}Cov(R_i, R_j)\), que é a média das covariâncias entre os ativos.

Assim, quando o número de ações na carteira tende ao infinito, segue:

Isto é, quando o número de ativos cresce muito a variância da carteira se aproxima do valor da média da covariância entre os ativos. Assim, o risco remanescente corresponde ao risco de mercado, o que está ilustrado no gráfico a seguir.

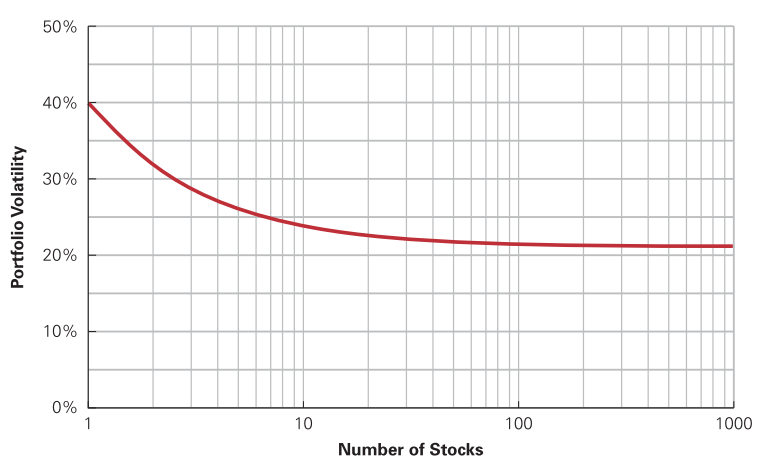
Fonte: BERK, 2014

Escolha de uma carteira

Não existe uma carteira que seja a melhor para todos investidores. Isso ocorre por que investidor têm preferências diferentes de combinação de risco e retorno, e tais preferências variam de acordo com fatores como idade, renda, estado civil e perspectivas futuras. Isto é, esses fatores podem tornar o agente mais ou menos avesso ao risco. Nesse contexto, a seleção de carteira consiste encontrar a carteira que melhor satisfaça a preferência do investidor dentre N carteiras diferentes.

Princípio da dominância

A diversificação permite a criação de diversas combinações de risco e retorno, e nem todas as carteiras diversificadas são eficientes. É possível realizar a comparação entre carteiras ou ativos que apresentem o mesmo risco ou o mesmo retorno. Essa comparação pode mostrar aquele ativo ou carteira que é mais eficiente, comparativamente, que os demais.

Supondo que no mercado existam as ações \(X\) e \(Y\), essas ações possuem o mesmo retorno, mas riscos distintos - o risco da ação \(Y\) é quatro vezes maior que o risco da ação \(X\). Se o investidor avaliar somente o retorno esperado, será indiferente entre os dois ativos. Entretanto, se esse investidor for racional e analisar tanto o retorno como o risco, optará pela ação \(X\), que está de acordo com o princípio da dominância. Esse princípio diz que: “um agente racional optará pelo investimento que lhe fornece o maior retorno esperado dado um nível de risco, ou o menor risco dado um nível de retorno”. Com isso é nítido que o ativo \(X\) domina o ativo \(Y\).

No gráfico abaixo, note que a ação da Coca-Cola apresenta um risco de 25%, assim como a ação da Bore. Todavia, o retorno apresentado pela Coca-Cola é maior. Logo, um investidor racional, ao se deparar com as duas ações no mercado, irá optar por aquela com maior retorno. Apesar de ser dominante, nenhuma dessas duas ações está sobre a fronteira de eficiência, portanto existe uma combinação que pode trazer um maior retorno, com o mesmo risco.

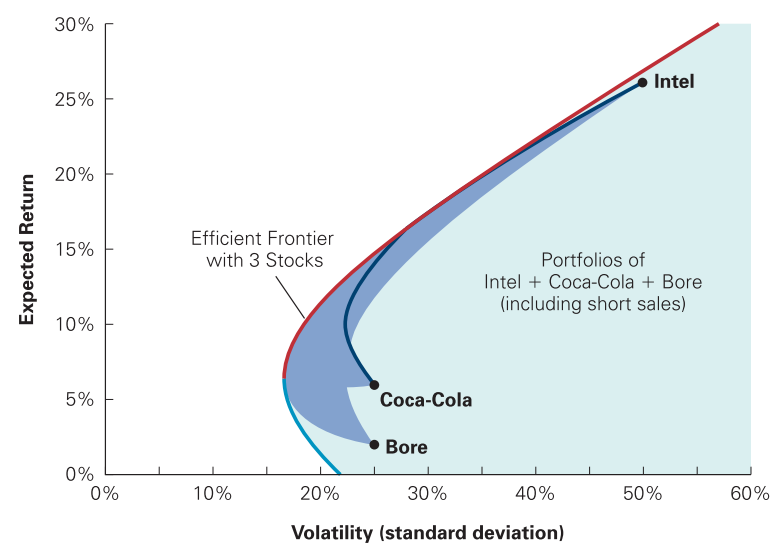
Fonte: BERK, 2014

Carteiras Eficientes

No exemplo anterior, o investidor escolheu a carteira composta com a ação da Coca Cola, uma vez que esta era dominante, dentre as opções que ele possui. Agora suponha que existe a carteira \(A\), que assim como as ações apresentadas, possui uma volatilidade de 25%, mas a carteira \(A\) representa a combinação de ativos com o maior retorno. Essa carteira será a carteira eficiente, uma vez que o investidor pode ficar numa melhor posição ao escolher \(A\), invés das demais carteiras.

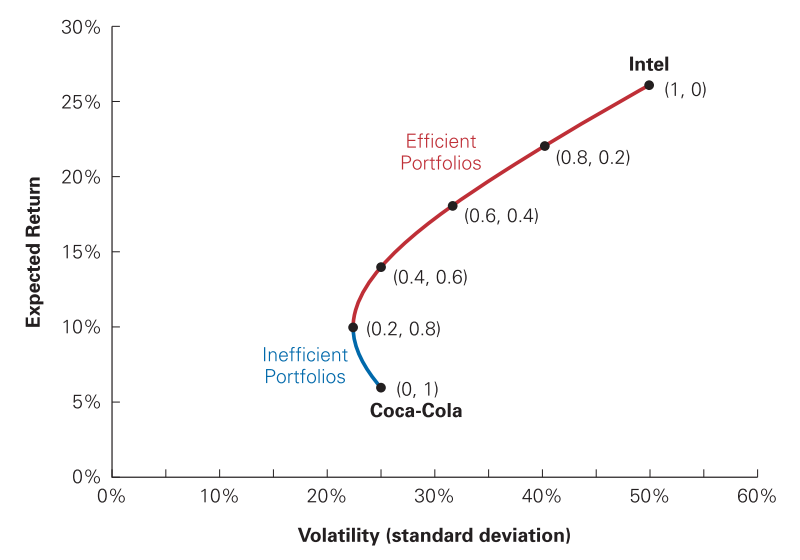
Fonte: BERK, 2014

Note que na combinação \((0,1)\), em que a carteira é composta apenas por ativos da Coca-Cola, o risco é o mesmo que no ponto \((0.4, 0.6)\), em que 40% da carteira é composta por ações da Intel e 60% por ações da Coca-Cola, essa carteira apresenta o mesmo risco, entretanto o retorno é maior e ela está posicionada na fronteira de eficiência, isso significa que um investidor racional que está disposto a aceitar 25% de volatilidade, irá optar pela combinação \((0.4, 0.6)\).

Uma carteira eficiente, portanto, pode ser definida como aquela que apresenta o maior retorno esperado dado um nível de risco. Ou, alternativamente, a carteira de menor risco dado um nível de retorno, isto é, a carteira de variância mínima. Essa é a carteira que um investidor racional irá escolher dentre as opções que foram apresentadas para ele.

Partindo da uma visão de carteira de variância mínima, o problema de selecionar uma carteira pode ser definido como um problema de otimização. Isto é, como encontrar a carteira de menor risco dado um retorno desejado. Matematicamente:

Sendo \(w\) o vetor de pesos da carteira a ser encontrada, \(M\) a matriz de covariância dos retornos, \(R\) o vetor com dos retornos de cada ativo, \(R_d\) o retorno desejado para a carteira ótima e \(\textbf1\) um vetor de cuja todas as coordenadas são 1. O problema de otimização tem duas restrições: \(wR=R_d\) e \(w\textbf{1}=1\). A primeira restrição afirma que a carteira ótima deve ter o retorno igual ao retorno desejado, já segunda afirma que a soma das participações de cada ativo deve somar 1.

Resolver tal problema de minimização significa encontrar a participação de cada ativo na carteira, os pesos, tal que a carteira tenha o menor risco entre todas as carteiras com os mesmos ativos e retorno igual \(R_d\).

Através dessa solução, variando os valores \(R_d\), pode-se representar em um espaço bidimensional de Variância x Retorno Esperado, todas as carteiras geradas essa representação apresenta a forma de uma hipérbole. Ademais, o problema de otimização de Markowitz é quadrático e convexo, o que garante que de fato o problema é solucionado de maneira eficiente.

O modelo de otimização de Markowitz também pode ser resolvido através da maximização do retorno dado um nível de risco. Assim, uma formulação equivalente ao problema de minimização é:

Usando termos de pesquisa operacional, diz-se que o problema de minimização de variância dado um nível de retorno desejado é o problema primal e o de maximização do retorno dado um nível de variância desejada, o seu dual.

Fronteira eficiente

Colocando todas as combinações de retorno e risco das possíveis carteiras de conjunto de ativos obtém-se o seguinte gráfico. Abaixo pode-se observar duas fronteiras eficientes, a fronteira eficiente de uma carteira contendo as 10 ativos, representada pela linha continua, a fronteira eficiente contendo 3 ativos, representada pela linha pontilhada. O eixo \(Y\) apresenta todos os retornos para cada combinação e o eixo \(X\) apresenta o risco para cada combinação de ativos.

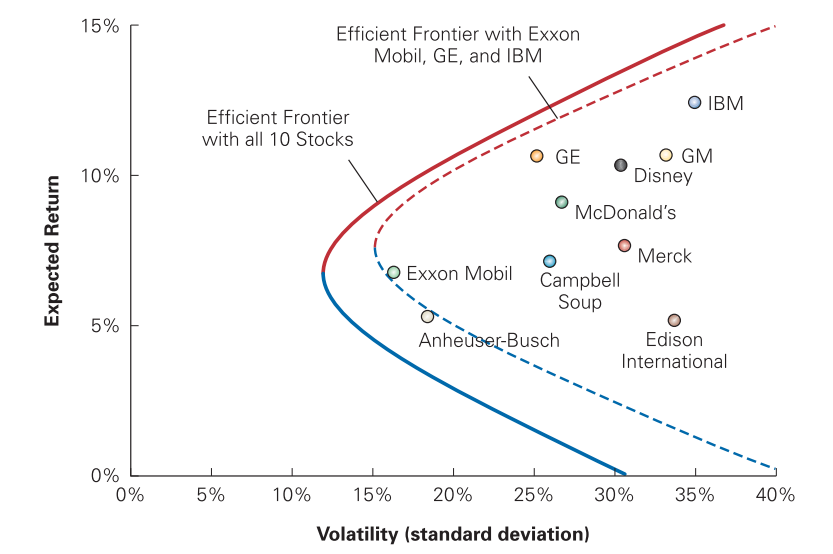
Fonte: BERK, 2014

Cada ponto no acima abaixo representa uma carteira. Dado um nível de risco desejado, o agente escolheria a carteira mais alta no gráfico e, dado um nível de retorno, o agente escolheria a carteira mais à esquerda no gráfico segundo o princípio da dominância. Essas escolhas são as carteiras eficientes e conjunto dessas carteiras é chamada de fronteira eficiente. No gráfico acima, as fronteiras eficientes são representadas pela cor vermelha.

Ademais, a fronteira eficiente tende a expandir à medida que se se aumenta a quantidade de ativos na carteira. Abaixo, na linha pontilhada, observa-se que uma fronteira formada apenas por três ativos é menor que a fronteira composta pelos 10 ativos, representada pela linha contínua. Essa expansão mostra que a diversificação pode ser benéfica.

Usando o R

Para ilustrar a discussão teórica feita até aqui, será usado o R para calcular uma fronteira eficiente para um conjunto de ativos.

Obtendo dados

Será necessário carregar os seguintes pacotes:

library(ggplot2)
library(magrittr)
library(quantmod)
library(xts)
library(tseries)
library(ggplot2)

Caso não possua esses pacotes instalados você pode usar install.packages('nome_pacote') para instalá-los e depois carregue eles usando os comandos acima. Além dos listados acima, será necessário que os pacotes tidyr e dplyr estejam instalados, entretanto, não é necessário carrega-los.

Usaremos os pacotes quantmod e xts para obter os dados de interesse e tratar-los para o objetivo que desejamos. Assim, para o exercício, vamos obter o dados para as seguintes ativos:

• ITSA4 - Itaú SA Investimentos;
• NATU3 - Natura;
• PETR4 - Petrobras;
• ABEV3 - Ambev SA.

Usaremos as funções do pacote quantmod para obter os preços diárias das ações entre outubro de 2016 e dezembro de 2019. Antes desse período, os dados do índice Bovespa apresenta muitos valores perdidos.

# Definindo parâmetros
simbolos <- c("ITSA4.SA", "VVAR3.SA", "FNOR11.SA", "PETR4.SA", "BOVV11.SA")

startdate <-  '2016-10-27' # Sys.Date() - 730
enddate <- '2019-12-15' # Sys.Date()

# Fazendo download
ativos <- new.env()

getSymbols(Symbols = simbolos, env = ativos, src = 'yahoo',
           from = startdate, to = enddate, auto.assign = TRUE)
ativos <- as.list(ativos)

Se tudo tiver corrido corretamente os dados das ações foram baixados em carregados no environment ativos que posteriormente foi transformando em uma lista. Usaremos lista frequentemente nesse exercício, elas simplificam bastante a transformação de dados ao permitir que uma operação seja realizada sobre todos os seu elementos usando a função lappy().

Processando os dados

Agora que temos os dados, vamos realizar um processamento de modo a obter o retorno mensais dessas séries, mas antes disso vamos que criar algumas funções para nos auxiliar nisso:

get_preco_fechamento <- function(x){
  ## Obtem preço de fechamento
  
  x[, base::grepl(pattern = '\\.Close$$', x = dimnames(x)[[2]])]
}

list_to_xts <- function(list_xts){
  ## Transforma uma lista de objetos xts em um objeto xts
  
  nomes <- names(list_xts)
  res <- do.call(cbind.xts, list_xts)
  dimnames(res)[[2]] <- nomes
  
  return(res)
}

xts_to_data.frame <- function(x){
  ## Transforma objeto xts em data.frame
  
  df <- as.data.frame(x)
  df <- data.frame(
    periodo = row.names(df),
    df
  )
  row.names(df) <- NULL
  
  return(df)
}

Na lista ativos estão os dados de transações de cada ativo na bolsa em objetos xts. Em cada objeto xts estão guardados informações como o menor preço alcançado pela ação no dia, o maior preço alcançado, o preço do ativo na abertura do pregão, o preço de fechamento e outras informações. Para nosso exercício, usaremos o preços de fechamento dos ativos e partir deles calcularemos os retornos mensais, por isso, precisamos da função get_preco_fechamento().

Já a função list_to_xts() recebe uma lista de objetos xts e a transforma em apenas um objeto xts e, por fim, a função xts_to_data.frame transforma um objeto xts em um data.frame mantendo o período dos dados como uma coluna do data.frame resultante. A seguir, vamos calcular os retornos mensais dos ativos:

#Obtendo apenas os preços de fechamento
ativos <- lapply(X = ativos, FUN = get_preco_fechamento)

# calculando retornos mensais
retornos_men <- lapply(ativos, quantmod::monthlyReturn)

# Juntando ativos em um objeto xts
carteira <- list_to_xts(retornos_men)

# Transformando objeto xts em uma matriz e retirando dados perdidos
carteira <-  as.matrix(carteira)
carteira <- na.omit(carteira)

Aplicando a função get_preco_fechamento() por meio da função lapply() obtemos uma lista com o preço de fechamento de cada ativo, procedimento semelhante foi feito para calcular o retorno mensal de cada ativo. Ao final, a matriz carteira representa a carteira contendo os retornos dos ativos.

Explorando dados

Antes de prosseguirmos, vamos dar uma olhada na evolução dos preços de fechamento dos ativos. Para isso, usaremos as seguintes funções:

precos_tidy <- function(data, periodo){
  ## Transforma os precos para o formato long
  
  cols <- base::setdiff(names(data), periodo)
  res <- tidyr::gather(data, key = 'ativo', value = 'precos', cols)
  
  res[, periodo] <- as.Date(as.character(res[[periodo]]))
  class(res) <- c('carteira', class(res))
  
  return(res)
  
}

plot_precos <- function(data, periodo, filter = NULL){
  ## Plota a evolução dos preços
  
  # Validação
  stopifnot('carteira' %in% class(data))
  
  # Quotando variável
  periodo <- dplyr::sym(periodo)
  
  # Filtrando ativos
  if(!is.null(filter)){
    data <- dplyr::filter(data, ativo %in% filter)
  }
  
  ggplot(data, aes(x = !!periodo, y = precos, color = ativo))+
    geom_line()+
    labs(
      x = '',
      y = 'Preço de fechamento',
      color = 'Ativo',
      title = 'Evolução dos ativos'
    )
}

Os dados dos ativos estão organizados de forma que cada coluna representa uma ativo diferente, nesse caso, diz-se que os dados estão num formato wide. Entretanto, o ggplot2 foi construído para seguir uma lógica em que os dados estão no formato long, também chamado de tidy. Nesse caso, os dados sobre os ativos são organizados em duas colunas: uma conterá o nome do ativo e outra o preço da ação correspondente respeitando o período da observação. A função precos_tidy() faz justamente essa transformação.

A função plot_precos() toma o preços no formato long e cria um gráfico usando as funções do ggplot2. A seguir, plotamos a evolução dos preços de fechamento das ações e calcular as correlações entres o preços.

precos_ <- precos_tidy(precos, 'periodo')

plot_precos(precos_, 'periodo')

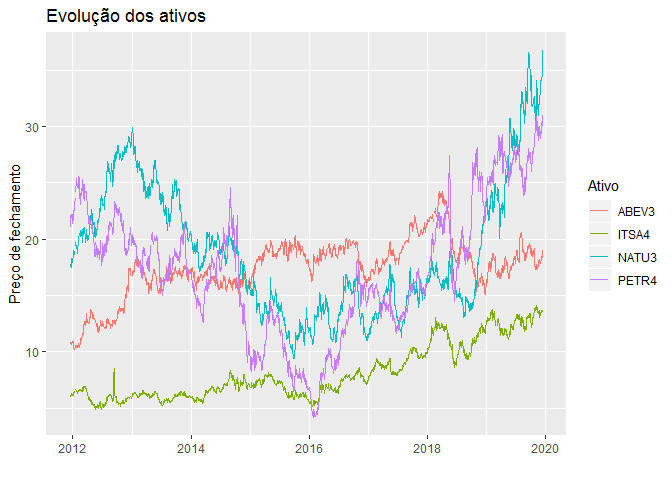
# calculando correlação entre os preços
m <- as.matrix(precos[, -1])
m <- na.omit(m)
cor(m)

##            ABEV3      NATU3      PETR4     ITSA4
## ABEV3  1.0000000 -0.3243479 -0.2361517 0.4825303
## NATU3 -0.3243479  1.0000000  0.7464562 0.2422055
## PETR4 -0.2361517  0.7464562  1.0000000 0.5854143
## ITSA4  0.4825303  0.2422055  0.5854143 1.0000000

Na tabela acima, cada célula representa a correlação entre os preços do ativo da linha com o ativo da coluna. Chama a atenção a alta correlação existente entre preços das ações da Petrobras, PETR4, e da Natura NATU3, que alcança o valor de 74,65%. Isso é um pouco curioso, já que essas empresas são de setores diferentes. Tal relação fica mais clara no gráfico a seguir:

plot_precos(precos_, 'periodo', filter = c('PETR4', 'NATU3'))

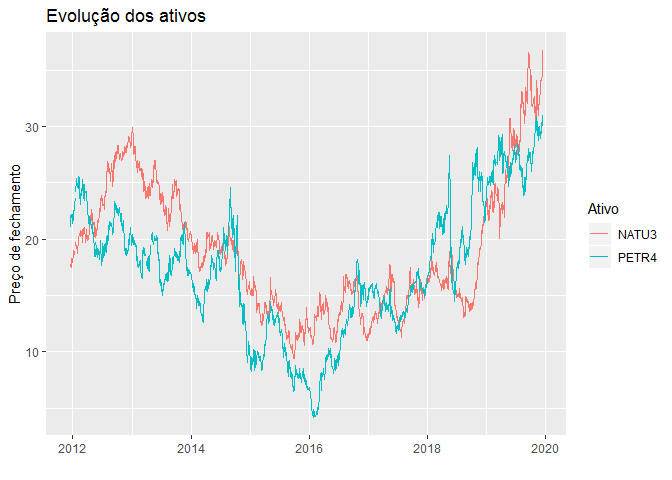
Os dois ativos apresentam a tendência de queda entre 2013 e meados de 2016, após esse período passa a ter uma tendência ascendente. Talvez a mudança de governo ocorrido em 2016 tenha sido um motivo relevante para esse comportamento. A apesar de tudo isso, a mesma relação não se mantém quando calculamos a correlação entre os retornos. Quando fazemos esse cálculo, percebemos que a maior correlação ocorre entre PETR4 e ITSA4 como pode ser visto abaixo:

# Correlação entre os retornos
cor(carteira)

##            ABEV3     NATU3      PETR4     ITSA4
## ABEV3 1.00000000 0.1066042 0.06589754 0.3241655
## NATU3 0.10660416 1.0000000 0.30124177 0.2985749
## PETR4 0.06589754 0.3012418 1.00000000 0.6686894
## ITSA4 0.32416546 0.2985749 0.66868936 1.0000000

Calculando fronteira eficiente

O pacote tseries possui uma função chamada portfolio.optim(). Dado um conjunto de ativos e um retorno esperado para a carteira, ela calcula a carteira de menor variância e retorna uma lista com os pesos de cada ativo na carteira ótima, o risco e o retorno esperado.

Usaremos essa função para calcular a fronteira eficiente para o 4 ativos escolhidos. Para o nosso objetivo, três argumentos será de particular interesse: x, pm e shorts. O argumento x recebe uma matriz com os retornos históricos dos ativos em cada coluna é uma ativo diferente; pm recebe o retorno desejado para carteira ótima escolhida e shorts recebe TRUE ou FALSE, TRUE quando é permitido a venda a descoberto de ativos e FALSE quando não.

A venda a descoberta consiste na venda de uma ação que o investidor não possui na sua carteira. Neste caso o peso correspondente à essa ação na carteira será negativa. Operar com venda a descoberta é útil quando se deseja alcançar um retorno que é maior (menor) que o maior (menor) retorno do ativo de maior (menor) retorno na carteira.

Para facilitar esse trabalho, vamos criar algumas funções:

carteira_otima <- function(ativos, retorno_desejado, shorts = FALSE){
  ## Calcula carteira ótima
  
  s <- tseries::portfolio.optim(
    x = ativos,
    pm = retorno_desejado,
    shorts = shorts
  )

  pesos <- s[['pw']]
  names(pesos) <- colnames(ativos)
  
  res <- list(
    pesos = pesos,
    retorno = s[['pm']],
    risco = s[['ps']]
  )
  
  return(res)
}

get_retorno <- function(res){
  ## Obtém o retorno da carteira ótima
  ## res: list
  
  sapply(res, `[[`, i = 'retorno')
}

get_risco <- function(res){
  ## Obtém o risco da carteira ótima
  ## res: list
  
  sapply(res, `[[`, i = 'risco')
}

Assim, a carteira ótima que tem o retorno mensal esperado de \(1\%\) seria dada por:

carteira_otima(ativos = carteira, retorno_desejado = .01, shorts = FALSE)

## $pesos
##     ABEV3     NATU3     PETR4     ITSA4 
## 0.5035733 0.2429710 0.0000000 0.2534557 
## 
## $retorno
## [1] 0.01
## 
## $risco
## [1] 0.04844689

Sendo pesos a participação de cada ativo na carteira ótima, retorno o retorno esperado e risco o desvio padrão esperado.

Vamos calcular o retorno esperados para o ativos e seus respectivos riscos e guardar tais informações em um data.frame. Após isso, vamos gerar um vetor de retornos desejados para as carteira ótimas a fim de gerar a fronteira eficiente.

retornos_esperados <- apply(carteira, MARGIN = 2, mean)
riscos <- apply(carteira, MARGIN = 2, sd)

ativos <- data.frame(
  acao = names(retornos_esperados),
  risco = riscos,
  retorno = retornos_esperados,
  row.names = NULL
)

ativos

##    acao      risco    retorno
## 1 ABEV3 0.05395006 0.00815532
## 2 NATU3 0.09332690 0.01254119
## 3 PETR4 0.13895500 0.01134941
## 4 ITSA4 0.07556379 0.01122900

Note que estamos estimando o retorno esperado dos ativos como sendo o média do retorno histórico, entretanto, essa é uma abordagem ingênua que implica em uma série de problemas como: não há garantias do que o que ocorreu no passado ocorrerá no futuro; dependendo do períodos observado, a média do retorno histórico é diferente.

As ações da ABEV3 a presentaram o menor retorno esperado, 0,8%, e o menor risco 5,4%. Já NATU3 apresenta o maior retorno esperado, 1,25%, entretanto, não apresenta o maior risco. Nesse caso, a máxima de que um maior risco implica em uma maior retorno nem sempre é válida quando estamos avaliando ativos individuais. Esse fato pode ser explicado pela distinção entre risco diversificável - idiossincrático - e não diversificável - risco sistêmico.

Para calcular a fronteira usaremos a função carteira_otima(). Ela toma como argumentos um conjunto de ativos e um retorno desejado e retorna a carteira com menor risco que possui o retorno igual ao retorno desejado. A fronteira eficiente é justamente o conjunto de carteiras com menor risco possível ao valor de retorno dado.

Portanto, para gerar a fronteira eficiente será necessário gerar esse conjunto de carteira ótimas. Para tanto, é necessário gerar um retorno desejado para cada carteira ótima. A seguir serão gerando 50 retornos desejados para gerar 50 carteiras ótimas e construir a fronteira eficiente.

retorno_min <- 0.5*min(retornos_esperados)
retorno_max <- 1.5*max(retornos_esperados)

retornos_seq <- seq(retorno_min, retorno_max, length.out = 50)

O menor retorno esperado tem a metade do retorno do ativo com menor retorno e o maior tem a metade a mais que do retorno esperado do ativo de maior rendimento. Assim, foram gerados 50 retornos desejados igualmente espaçados.

A seguir calcularemos as carteiras da fronteira. Como há retornos desejados abaixo e acima dos retornos mínimo e máximo dos ativos na carteira usaremos short = TRUE.

# Primeira com todos os ativos
fronteira <- lapply(
  X = retornos_seq,
  FUN = carteira_otima,
  ativos = carteira,
  shorts = TRUE
)

# Fronteira sem NATU3
nomes_ativ <- c("ABEV3", "PETR4", "ITSA4")
fronteira2 <- lapply(
  X = retornos_seq,
  FUN = carteira_otima,
  ativos = carteira[, nomes_ativ],
  shorts = TRUE
)

# Criando data frame
dados_plot <- data.frame(
  retorno = get_retorno(fronteira),
  risco = get_risco(fronteira),
  retorno2 = get_retorno(fronteira2),
  risco2 = get_risco(fronteira2)
)

O data.frame dados_plot contêm o dados de risco e retorno das carteiras ótimas. Com eles é possível plotar a fronteira eficiente, como poder ser visto no gráfico a seguir:

# Plotando fronteira eficiente
dados_plot %>% 
  ggplot(aes(x = retorno, y = risco, color = '#E7B800'))+
  geom_line(size = 1)+
  geom_line(size = 1, aes(y = risco2), color = '#5F9EA0')+
  geom_point(data = ativos, aes(x = retorno, y = risco, color = acao))+
  geom_text(data = ativos, aes(x = retorno, y = risco, label = acao, color = acao))+
  coord_flip()+
  labs(
    x = 'Retorno',
    y = 'Risco',
    title = 'Fronteira Eficiente',
    color = ''
  )+
  theme(legend.position = 'none')

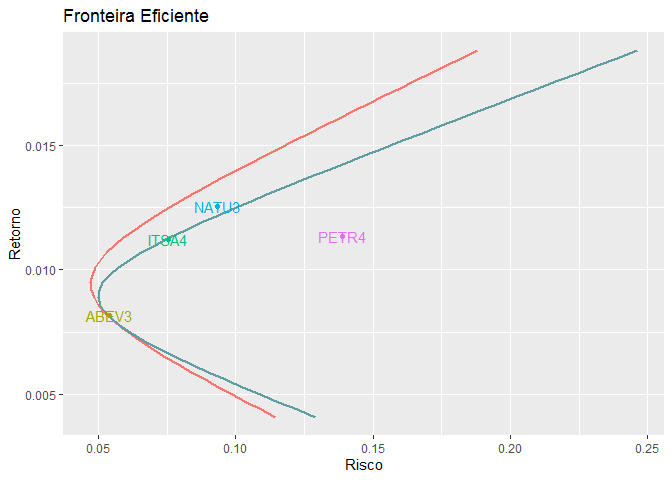
A fronteira mais escura foi construída a partir dos ativos ABEV3, PETR4 e ITSA4, já a fronteira laranja foi construída com os mesmo ativos mais o ativo NATU3. A nova fronteira ficou mais à esquerda que a anterior, portanto, é possível obter o mesmo retorno com uma risco menor por meio dessa nova nova fronteira eficiente. Tais resultados são possíveis devido aos efeitos da diversificação: ao aumentar a quantidade de ativos na carteira, o risco cai mais que os retornos ponderados dos ativos.

Os scripts usados ao longo do post estão disponíveis no GitHub

Fontes consultadas

BERK, Jonathan B.;DEMARZO, Peter. Corporate finance. 3rd ed. Peason, 2014.

ROSS, Stephen A. et al.Fundamentos de administração financeira. 9 ed. Porto Alegre: AMGH, 2013.

BREALEY, Richard A.; MYERS, Stewart C.; ALLEN, Franklin. Princípios de finanças corporativas. 10 ed. Porto Alegre: AMGH, 2013.

• ← Previous Post
• Next Post →