Table of Contents
[TOCM]
[TOC]
Parte I – Estatística experimental e estatística observacional
Uma aplicação de ferramentas estatísticas é a avaliação da eficácia de uma intervenção, tratamento ou política de ação. Ao separar os indivíduos de nossa amostra em dois grupos, trata-los de forma distinta, e estuda-los com respeito aos resultados obtidos, podemos inferir em como atua o tratamento em questão. Em um simples caso binário, temos um grupo que receberá o tratamento – denominado grupo de tratamento – e outro que não receberá o tratamento – o grupo de controle. Ao comparar os resultados ao fim de um determinado período e aplicar as devidas ferramentas estatísticas, poderemos determinar quão bem sucedido é o tratamento, dada a amostra em questão.
Como os dados chegam ao pesquisador? Eles podem ser provenientes de experimentos ou pela observação, caso no qual as variáveis independentes (isto é, explicativas) não estão sob controle do pesquisador. Um detalhe de grande importância quando da realização de estudos estatísticos é garantir a minimização de vieses, que podem surgir de várias formas. No caso aqui em discussão, uma fonte de viés pode surgir do modo como cada indivíduo é escolhido/alocado a pertencer a determinado grupo de estudo. Uma alocação enviesada pode ocasionar erros de inferência, já que a amostra não é representativa da população que se quer analisar, consequentemente tornando os resultados menos confiáveis, ou mesmo falsos, do ponto de vista estatístico. Queremos, portanto, encontrar modelos que auxiliem a solucionar esse problema de viés de seleção e que possam providenciar estimativas válidas do efeito médio de tratamento (Average Treatment Effect – ATE).
O ATE é calculado tomando-se a diferença da média entre os resultados obtidos no grupo de controle e grupo de tratamento; desta forma, obtemos uma medida dos efeitos entre ambos os grupos e podemos avaliar a eficácia do tratamento nos indivíduos.
Randomized Control Trials (RCT) são experimentos nos quais a alocação é randomizada – isso significa que a probabilidade do indivíduo pertencer ao grupo de controle ou ao grupo de tratamento é a mesma (50%) em nosso exemplo binário. A garantia de randomização diminui o risco de viés na análise, assim como de associações espúrias, já que temos uma maior certeza em afirmar que os grupos são parecidos em tudo, exceto sua exposição ao tratamento. Contudo, nem sempre a realização de um RCT é possível: os custos podem ser proibitivamente elevados, e em muitos casos o tema de estudo esbarra em questões éticas, inviabilizando a realização de experimentos.
Parte II – O Propensity Score Matching
Quando não é possível randomizar a alocação dos indivíduos aos grupos, como no caso de estudos observacionais, não se pode realizar inferências causais, já que não é possível determinar se a diferença de resultados entre os grupos de tratamento e controle são provenientes de diferenças “ao acaso” entre os indivíduos participantes do estudo ou se são diferenças sistemáticas.
Devido a essas limitações, o Propensity Score Matching (PSM) é uma alternativa para estimar os efeitos causais de receber o tratamento em uma amostra de indivíduos. O método PSM foi introduzido na literatura por Paul Rosenbaum e Donald Rubin em 1983; a ideia é de atribuir uma probabilidade de receber o tratamento a cada indivíduo da amostra – o propensity score (PS) –, controlando para suas características observadas, e depois parear unidades de ambos os grupos com propensity scores similares, para em seguida comparar os resultados obtidos entre os pares. O modelo pode ajudar a solucionar o problema de viés de seleção e providenciar estimativas não enviesadas do efeito médio do tratamento.
O propensity score é uma probabilidade condicional de que o participante de um estudo receba o tratamento dadas as covariáveis observadas; assim, não só aos participantes que de fato receberam o tratamento lhes é atribuído um propensity score, mas àqueles que não receberam também lhes é atribuída essa probabilidade. Além disso, condicionando para o PS, cada participante apresenta a mesma probabilidade de alocação para o tratamento, assim como em um experimento randomizado. O propensity score pode ser encarado como um balancing score (cujo conceito é explicado mais à frente) representante de um conjunto de covariáveis; deste modo, um par de indivíduos do grupo de controle e de tratamento que apresentem um propensity score similar podem ser comparáveis, mesmo que apresentem diferenças nas covariáveis específicas.
O viés quando da estimação do ATE surge quando diferenças nos resultados possam ser consequência de caracterísiticas secundárias dos indivíduos do que realmente em razão do tratamento aplicado. O cenário ideal para mitigação desse problema seria a realização de um RCT, dado que a randomização permite balancear essas caracterísiticas secundárias quando da alocação nos grupos de tratamento ou controle. O método PSM surge como alternativa à realização de um RCT, na medida em que simula um experimento controlado; a atribuição de probabilidades aos indivíduos-teste de receber o tratamento influi no sentido de enfrentar o problema de viés de seleção e viés dos estimadores do ATE, já que por esse método estaremos comparando agentes com caracterísiticas semelhantes, porém diferentes quanto à sua participação no grupo de tratamento. Assim, a análise é realizada entre uma seleção de indivíduos de ambos os grupo com relativo grau de paridade – e, esperamos, comparabilidade – em termos de covariáveis observada.
Uma diferença chave entre os dois métodos, contudo, é que enquanto o RCT realiza um balanceamento para todas as caracterísitcas secundárias dos indivíduos, sejam eles participantes ou não do grupo de tratamento, o PSM permite somente o balanceamento daquelas características observáveis pelo pesquisador no momento do estudo. Aquilo que não for observável não será levado em consideração quando do cálculo das probabilidades condicionais, sendo portanto uma potencial fonte de viés quando da estimação do ATE.
Como dito anteriormente, o propensity score é uma medida de equilíbrio que sumariza a informação do vetor de covariáveis. Participantes do grupo de controle e do grupo de tratamento com o mesmo valor do propensity score têm a mesma distribuição das covariáves observadas; ou seja, em um set de pares que é homogêneo para o PS, ambos os indivíduos podem apresentar valores diferentes para as covariáveis, mas essas diferenças serão puramente por acaso, e não diferenças sistemáticas.
Parte III – Exemplos simples
O PSM pode ser aplicado a uma ampla gama de campos de estudo, desde análises na biologia e medicina, até mesmo em aplicações nas ciências sociais. Sejam os seguintes exemplos:
- Queremos avaliar a eficácia de um determinado tratamento médico em meio a uma amostra de pacientes que padeceram de uma doença. Ao seguir a metodologia do PSM, atribuiremos Z=1 àqueles pacientes que receberam o tratamento, e Z=0 àqueles que não receberam. Ao compararmos pacientes com características semelhantes, poderemos determinar o grau de sucesso do tratamento.
- Queremos avaliar a eficácia da adoção do regime de metas de inflação no combate à inflação. Seja a variável binária Z; Z=1 para países que adotam esse regime de metas, e Z=0 para aqueles que não adotam. Ao aplicarmos a metodologia do PSM, poderemos comparar países em cada grupo semelhantes quanto às variáveis independentes escolhidas, de forma a determinar o grau de sucesso dessa política em reduzir a taxa de inflação.
Parte IV – Run-through metodológico simples
Criamos aqui então um exemplo hipotético, mas atual para que pudéssemos entender aplicações do PSM. Imagine que queiramos entender o efeito do tratamento de da Cloroquina no tempo de recuperação de pacientes que tiveram o COVID-19 afim de enterdemos se essa intervenção/tratamento realmente tem eficácia.
Com isso criamos uma** base fake** com as seguintes colunas:
- Febre (X) - Sintoma
- Idade (X) - Sintoma
- Sexo (X) - Sintoma
- Dor no peito (X) - Sintoma
- Dificuldade Respirar (X) - Sintoma
- Cloroquina (A) - Intervenção
- Tempo Recuperação (Y) - Variável a ser analisada
Passo 1 - Importar as bibliotecas
Mesmo importando algumas bibliotecas aqui agora, estarei importando ao longo do código para facilitar a compreensão, mas já importarei algumas bibliotecas que podem ser necessárias no trato das informações que usaremos
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
%matplotlib inline
Passo 2 - Bases + Logistic Regression
Para calcular o propensity score, podemos fazer uso de um modelo de regressão logística ou de um modelo probit. Adicionamos covariáveis observadas apropriadas no modelo e com isso obtemos uma probabilidade de exposição ao tratamento para toda a amostra. É importante notar que, quando da construção do modelo, as variáveis a serem incluídas não devem ser efeitos do tratamento, e sim preditoras do resultado; podemos incluir termos de interação e não precisamos nos importar com parcimônia ou perda de graus de liberdade.
Mas antes vamos estar tratando algumas informações para enfim aplicarmos a regressão logística
base = pd.read_excel("Oficina_PSM.xlsx") #abre a base
## Tratamos o nosso X
x = base[["Febre_(X)",'Idade_(X)','Sexo_(X)',"Dor_no_peito_(X)",'Dificuldade_Respirar_(X)']] #escolhe as colunas que queremos
X = x.values #transformamos em matriz
## Tratamos o nosso Y
y = base[["Cloroquina_(A)"]] #escolhe as colunas que queremos até a intervenção
y = y.values #transformamos em vetor
x.describe() #descreve a base
| Febre_(X) | Idade_(X) | Sexo_(X) | Dor_no_peito_(X) | Dificuldade_Respirar_(X) | |
|---|---|---|---|---|---|
| count | 100.000000 | 100.00000 | 100.000000 | 100.000000 | 100.000000 |
| mean | 0.470000 | 55.45000 | 0.490000 | 0.560000 | 0.580000 |
| std | 0.501614 | 20.39973 | 0.502418 | 0.498888 | 0.496045 |
| min | 0.000000 | 20.00000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 0.000000 | 38.75000 | 0.000000 | 0.000000 | 0.000000 |
| 50% | 0.000000 | 54.00000 | 0.000000 | 1.000000 | 1.000000 |
| 75% | 1.000000 | 73.25000 | 1.000000 | 1.000000 | 1.000000 |
| max | 1.000000 | 90.00000 | 1.000000 | 1.000000 | 1.000000 |
Antes de estimar os efeitos do tratamento, temos de ajustar os propensity scores para diferenças entre os grupos de tratamento. Devemos checar se os propensity scores nos permitem balancear a distribuição das variáveis explicativas com respeito aos dois grupos; um balancing score (b(x)) é uma função das covariáveis (x) tal que a distribuição condicional das covariáveis dado b(x) é similar para ambos os grupos de estudo (de tratamento e de controle). Isso pode ser observado em um gráfico de distribuição das variáveis explicativas dentro de quintis do propensity score para ambos os grupos.
Um conceito importante é o de forte ignorabilidade (strong ignorability); se a alocação ao tratamento é fortemente ignorável dadas as covariáveis, então os resultados são condicionalmente independentes da variável binária Z (que indica a exposição ou não ao tratamento) dadas as variáveis explicativas. Feito isso aplicamos a regressão logística e teremos o scores.
clf = LogisticRegression(random_state=0).fit(X, y) #define o modelo
score = pd.DataFrame(clf.predict_proba(X), columns = (["P(0)","P(1)"])) #estimamos os scores
score = score[["P(1)"]] #utilizamos somente o score referente a probabilidade do tratamento
base_identidade = pd.concat([base, score], axis=1)#concateno as bases
base_score = base_identidade[["P(1)","Cloroquina_(A)"]] #crio uma base específica
base_tempo = base_identidade[["P(1)","Cloroquina_(A)","Tempo_Recuperação_(Y)"]] #crio uma base específica
base_identidade
| Febre_(X) | Idade_(X) | Sexo_(X) | Dor_no_peito_(X) | Dificuldade_Respirar_(X) | Cloroquina_(A) | Tempo_Recuperação_(Y) | P(1) | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 78 | 0 | 1 | 0 | 0 | 26 | 0.215053 |
| 1 | 1 | 88 | 1 | 1 | 1 | 0 | 20 | 0.434960 |
| 2 | 0 | 36 | 1 | 1 | 1 | 1 | 14 | 0.512854 |
| 3 | 0 | 69 | 1 | 1 | 0 | 0 | 20 | 0.313836 |
| 4 | 1 | 84 | 1 | 0 | 0 | 1 | 11 | 0.459133 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 95 | 1 | 81 | 1 | 0 | 1 | 1 | 22 | 0.581955 |
| 96 | 1 | 74 | 0 | 0 | 0 | 1 | 13 | 0.386607 |
| 97 | 0 | 40 | 1 | 1 | 1 | 1 | 11 | 0.501556 |
| 98 | 1 | 21 | 0 | 0 | 1 | 1 | 12 | 0.645221 |
| 99 | 0 | 45 | 1 | 1 | 0 | 1 | 23 | 0.374955 |
100 rows × 8 columns
Overlap
Então analisamos como estão os nossos dados através da etapa do Overlap. Um bom overlap significa que em qualquer lugar que olhemos da imagem teremos chance de acontecimento para os dois casos. E podemos ver que nesse exemplo ficou um pouco assim, pois se pegarmos qualquer lugar no gráfico teremos elementos para de ambos conjuntos, como veremos no gráfico mais abaixo.
selecao_tratados = base_score.loc[base_score['Cloroquina_(A)'].isin([1])] #filtro a base
selecao_tratados_tempo = base_tempo.loc[base_score['Cloroquina_(A)'].isin([1])] #filtro a base
selecao_tratados = selecao_tratados[["P(1)"]] #renomeio a coluna
selecao_n_tratados = base_score.loc[base_score['Cloroquina_(A)'].isin([0])] #filtro a base
selecao_n_tratados_tempo = base_tempo.loc[base_score['Cloroquina_(A)'].isin([0])] #filtro a base
selecao_n_tratados = selecao_n_tratados[["P(1)"]] #renomeio a coluna
print("Tratados %s e Não tratados:%s"% (selecao_tratados.shape[0],selecao_n_tratados.shape[0]))
Output: Tratados 45 e Não tratados:55
import seaborn as sns
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = 10, 6 #arruma fonte
plt.rcParams['font.size'] = 13 #arruma fonte
sns.distplot(selecao_n_tratados, label='Não Tratados') #não tratados
sns.distplot(selecao_tratados, label='Tratados') ##tratados
plt.xlim(0, 1) #escala
plt.title('Ditribuição do Propensity Score para Não tratados vs Tratados')
plt.ylabel('Densidade')
plt.xlabel('Scores')
plt.legend()
plt.tight_layout()
plt.show()
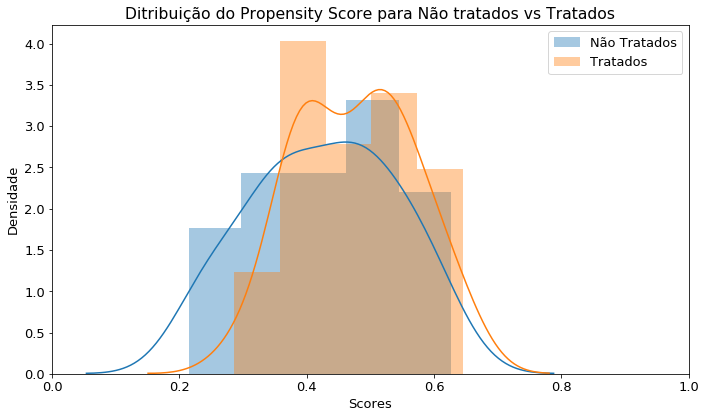
Matching
Em seguida, pareamos os indivíduos de grupos distintos com base em similitude de propensity score (ou seja, realizamos um match de um indivíduo do grupo de tratamento com um do grupo de controle). Existem vários métodos de pareamento – nearest neighbour, greedy matching, caliper matching, kernel matching, stratified matching, etc; a escolha do procedimento cabe ao pesquisador. O pareamento tipicamente leva a uma perda por descarte de indivíduos da amostra original; assim, o processo de pareamento também é uma forma de reamostragem.
#rodamos o modelo de vizinhos mais próximos
from sklearn.neighbors import NearestNeighbors
knn = NearestNeighbors(n_neighbors=1) #importa o modelo
knn.fit(selecao_n_tratados.values.reshape(-1, 1)) # faz o fit
distances, indices = knn.kneighbors(selecao_tratados.values.reshape(-1, 1)) #aplico o modelo
#transformo em datafram
indices = pd.DataFrame(indices, columns = {"Indices"}) #crio o dataframe
selecao_tratados = pd.DataFrame(selecao_tratados)
#### Processo de identificacao dos Matching
### merge do tempo Y para os tratados
lista_1 = [] #crio lista
lista_2 = [] #crio lista
for i in indices.Indices:#preencho a lista
lista_1.append(i)
for i in selecao_tratados["P(1)"]:#preencho a lista
lista_2.append(i)
tratados = pd.DataFrame(list(zip(lista_1, lista_2)),
columns =['Indices','Scores_Tratados'])
### merge do tempo Y para os tratados
lista_1 = [] #crio lista
for i in selecao_tratados_tempo["Tempo_Recuperação_(Y)"]:#preencho a lista
lista_1.append(i)
tratados_tempo = pd.DataFrame(list(zip(lista_1)),
columns =['Tempo_Recuperação_(Y)'])
### merge do tempo Y para os não tratados
lista_3 = []
lista_4 = []
a=0
for i in selecao_n_tratados_tempo["P(1)"]:#preencho a lista
a+= 1 #regra para novo indice
lista_3.append(a)
for i in selecao_n_tratados_tempo["P(1)"]: #preencho a lista
lista_4.append(i) #faço o append
n_tratados = pd.DataFrame(list(zip(lista_3, lista_4)),
columns =['Indices','Score_Nao_Tratados']) #unifico as listas
lista_3 = []
lista_4 = []
a=0
for i in selecao_n_tratados_tempo["P(1)"]:#preencho a lista
a+= 1 #regra para novo indice
lista_3.append(a)
for i in selecao_n_tratados_tempo["Tempo_Recuperação_(Y)"]: #preencho a lista
lista_4.append(i) #faço o append
n_tratados_tempo = pd.DataFrame(list(zip(lista_3, lista_4)),
columns =['Indices','Tempo_Recuperação_(Y)_N']) #unifico as listas
base_indices_Score = tratados.merge(n_tratados, on='Indices',right_index=True, how='left') #mesclo os matches para verificação
base_indices_tempo = base_indices_Score.merge(n_tratados_tempo, on='Indices',right_index=True, how='left') #mesclo os matches para verificação
#### Processo de identificacao dos Matching Finalizado
base_indices_tempo_final = pd.concat([base_indices_tempo, tratados_tempo], axis=1, join='inner') #concateno os dataframes
base_indices_tempo_final["Cloroquina_(A)_T"] = 1
base_indices_tempo_final["Cloroquina_(A)_NT"] = 0
#Agora já temos a base geral, mas precisamos ajeita-la, padronizando as colunas que representam a mesma coisa
base_indices_tempo_final.head()
| Indices | Scores_Tratados | Score_Nao_Tratados | Tempo_Recuperação_(Y)_N | Tempo_Recuperação_(Y) | Cloroquina_(A)_T | Cloroquina_(A)_NT | |
|---|---|---|---|---|---|---|---|
| 0 | 48 | 0.512854 | 0.509889 | 29 | 14 | 1 | 0 |
| 1 | 8 | 0.459133 | 0.457321 | 28 | 11 | 1 | 0 |
| 2 | 29 | 0.357378 | 0.356476 | 17 | 24 | 1 | 0 |
| 3 | 45 | 0.555223 | 0.555844 | 11 | 20 | 1 | 0 |
| 4 | 28 | 0.484609 | 0.481999 | 29 | 11 | 1 | 0 |
O que é essa base?
- Indices = Indice do score nao tratado gerado pelo KNN
- Scores_Tratados = Scores_Tratados
- Scores_Nao_Tratados = Scores_Nao_Tratados
- Tempo_Recuperação_(Y)_N = Tempo de recuperacao para os n_tratados
- Tempo_Recuperação_(Y) = Tempo de recuperacao para os tratados
- Cloroquina_(A)_T = Cloroquina para os tratados
- Cloroquina_(A)_T = Cloroquina para os n_tratados
tratados = base_indices_tempo_final[["Scores_Tratados","Cloroquina_(A)_T","Tempo_Recuperação_(Y)"]] #filtro as colunas que eu
#quero
tratados.columns = ["Score","Cloroquina_(A)","Tempo_Recuperação_(Y)"] #renomeio as colunas
n_tratados = base_indices_tempo_final[["Score_Nao_Tratados","Cloroquina_(A)_NT","Tempo_Recuperação_(Y)_N"]]#filtro as colunas que eu
#quero
n_tratados.columns = ["Score","Cloroquina_(A)","Tempo_Recuperação_(Y)"] #renomeio as colunas
# Geramos nossa babse final com todos os casos encaixados nas tres variaveis
base_final_1 = tratados.append(n_tratados)
base_final_1.describe()
| Score | Cloroquina_(A) | Tempo_Recuperação_(Y) | |
|---|---|---|---|
| count | 90.000000 | 90.000000 | 90.000000 |
| mean | 0.476043 | 0.500000 | 18.733333 |
| std | 0.090493 | 0.502801 | 6.363166 |
| min | 0.273230 | 0.000000 | 10.000000 |
| 25% | 0.397510 | 0.000000 | 12.000000 |
| 50% | 0.485462 | 0.500000 | 18.000000 |
| 75% | 0.551437 | 1.000000 | 23.750000 |
| max | 0.645221 | 1.000000 | 30.000000 |
Após o Matching
Poderíamos usar o Caliper que basicamente é a a distância que iremos tolerar entre os matches, filtrando assim melhor a base. Mas nesse caso não usaremos. Vamos dar uma olhada como ficou o gráfico após o match:
plt.rcParams['figure.figsize'] = 10, 6 #arruma fonte
plt.rcParams['font.size'] = 13 #arruma fonte
sns.distplot(n_tratados["Score"], label='Não Tratados') #não tratados
sns.distplot(selecao_tratados, label='Tratados') ##tratados
plt.xlim(0, 1) #escala
plt.title('Ditribuição do Propensity Score para Não tratados vs Tratados')
plt.ylabel('Densidade')
plt.xlabel('Scores')
plt.legend()
plt.tight_layout()
plt.show()
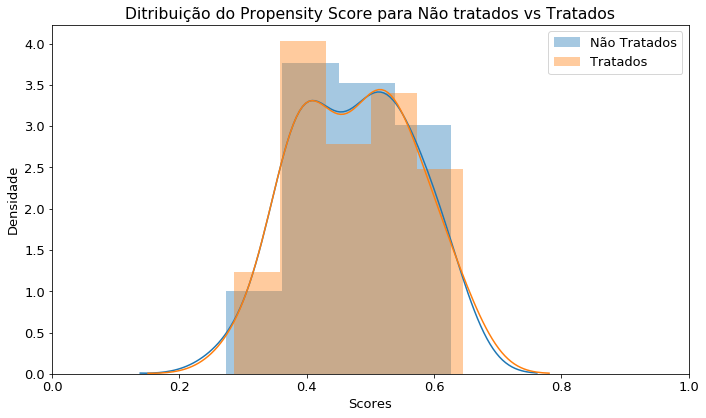
Um pouco diferente, não?
Por fim, calculamos então a média do efeito do tratamento por meio de uma análise multivariada dentro dessa nova amostra. A média da diferença dos resultados entre os pares é uma medida não enviesada do efeito médio do tratamento.
Nesse momento então tiramos a prova conceito adaptando ao modelo de reg linear e vendo seus p-valor e o seu beta
import statsmodels.api as sm #chamo o modelo
X_base= base_final_1[["Score", "Cloroquina_(A)"]] #filtro as colunas
y_base= base_final_1[["Tempo_Recuperação_(Y)"]] #filtro as colunas
X = sm.add_constant(X_base.values.ravel()) #aplicamos o modelo
results = sm.OLS(y_base,X_base).fit() #computamos os resultados
results.summary() #visualizamos os resultados
| Dep. Variable: | Tempo_Recuperação_(Y) | R-squared: | 0.856 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.853 |
| Method: | Least Squares | F-statistic: | 261.5 |
| Date: | Sun, 26 Apr 2020 | Prob (F-statistic): | 9.37e-38 |
| Time: | 00:22:57 | Log-Likelihood: | -309.10 |
| No. Observations: | 90 | AIC: | 622.2 |
| Df Residuals: | 88 | BIC: | 627.2 |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Score | 35.8065 | 2.301 | 15.564 | 0.000 | 31.235 | 40.378 |
| Cloroquina_(A) | 1.8723 | 1.576 | 1.188 | 0.238 | -1.260 | 5.005 |
| Omnibus: | 19.945 | Durbin-Watson: | 2.153 |
|---|---|---|---|
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 4.685 |
| Skew: | 0.014 | Prob(JB): | 0.0961 |
| Kurtosis: | 1.883 | Cond. No. | 2.60 |
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Conclusão do Exemplo
Em geral testamos a hipótese nula: O tratamento não tem efeito.
Se rejeitarmos a hipótese nula, dizemos que ele tem efeito. Em termos pratico, um p-valor abaixo de 0.05 nos leva a rejeitar a hipótese nula, essa hipótese é testada em cima daquele coeficiente beta ( 1.8723 ). Então a conta que ele faz é ( Beta / Erro padrão ). Na tabela, 1.8723 / 1.576 que irá dar exatamente o valor t.
| Ai olhamos a probabilidade desse valor ocorrer um valor maior que | t | -> (**P> | t | ), ou seja, maior que t positivo e menor que t negativo, se ela for alta (em termos práticos, acima de 0.05) dizemos que esse Beta não é diferente de zero, ou seja, **nesse caso FICTÍCIO o tratamento não tem efeito. |
Parte V – Vantagens e desvantagens do PSM
Dentre as principais vantagens do PSM, podemos incluir: a sumarização dos dados em uma “pontuação”, o propensity score, para estimar os efeitos do tratamento ao invés de observar e comparar múltiplas covariáveis; a amostra de indivíduos participantes do estudo pode ser mais representativa da população do que em um RCT; o cálculo do PS não inclui qualquer informação do resultado, logo a estimação do efeito do tratamento não sofre viés; como o modelo usado para estimar o PS não é o foco do estudo, ele não necessita ser parcimonioso, o que permite a inclusão de um número maior de covariáveis e termos de interação entre elas; entre outros.
As principais desvantagens do PSM surgem a partir de sua natureza não randômica de alocação dos indivíduos aos grupos de controle ou tratamento. De fato, o método PSM balanceia a análise com base em covariáveis observadas, enquanto experimentos randômicos balanceiam tanto sobre covariáveis conhecidas como desconhecidas. Ao não controlar para covariáveis desconhecidas, há o risco de viés afetando a probabilidade dos indivíduos receberam tratamento ou não. Além disso, é preferível, senão necessário, que o método seja aplicado em amostras grandes. Há a necessidade de sobreposição significativa entre os propensity scores dos grupos, de modo a melhor realizar o pareamento. O próprio pareamento, ao ser feito apenas em observância das variáveis observadas, abre a possibilidade de aumento do viés devido à existência de covariáveis não observadas.
Referências
- COWLING, Ben. Propensity Score Analysis. The University of Hong Kong. 2017. Disponível em : http://web.hku.hk/~bcowling/examples/propensity.htm
- FRASER, Mark W.; GUO, Shenyang. Propensity Score Analysis: statistical methods and applications - 2nd edition. SAGE Publications, 2015.
- PROPENSITY score. Columbia Mailman School of Public Health, 2012. Disponível em: https://www.mailman.columbia.edu/research/population-health-methods/propensityscore
- PROPENSITY Score Matching: Definition & Overview . Statistics How To, 2017. Disponível em: https://www.statisticshowto.com/propensity-score-matching/
- THAVANESWARAN, Arane. Propensity Score Matching in Observational Studies. Faculty of Health and Sciences, University of Manitoba, 2008. Disponível em: https://www.umanitoba.ca/faculties/health_sciences/medicine/units/chs/departmental_units/mchp/protocol/media/propensity_score_matching.pdf
- ROSEMBAUM, Paul R.; RUBIN, Donald B. The central role of the propensity score in observational studies for causal effects. Biometrika, 1983; 70:41-55