Um Olhar Descontraído Sobre o Dilema Viés-Variância
Fazer previsões é uma das principais ambições do ser humano. Uma pessoa pode ter a motivação de saber prever quase qualquer coisa, desde o placar de um evento esportivo até o preço de uma ação ou o humor da sua namorada… Mas o futuro é uma variável aleatória – ninguém sabe de fato como vai ser, qualquer previsão é em essência um “chute”. Bem, como chutar então? Você pode simplesmente jogar uma moeda, isso é bem conveniente, mas certamente não dá o melhor chute possível. É aí que entra a estatística, uma área do conhecimento que defino sucintamente como “a ciência do chute”.
Enquanto o futuro é um inerente mistério, o passado é um ambiente onde não há mais incerteza, então nada mais natural e sensato que tentar prever o futuro com base no que já aconteceu. A grosso modo, com base em potenciais elementos (uma lista de \(x_1,x_2,...,x_k\) variáveis independentes) que influenciem essa variável que se deseja prever (uma variável dependente \(y\)), tentar chutar valores futuros de \(y\) ao se coletar novos valores dos \(x\)’s (em aprendizado de máquina, o jargão para isso é “aprendizagem supervisionada”). Ou seja, a estatística busca fornecer o melhor chute, condicionado às informações disponíveis.
Pense intuitivamente: por mais que o futuro possa trazer uma coisa completamente diferente de tudo que já foi visto, é razoável assumir que o futuro e o passado compartilham de certos padrões, conexões que fazem as duas instâncias temporais serem manifestações de um mesmo fenômeno. Para obter bons chutes, um conceito bem importante é o chamado dilema viés-variância.
O que isso quer dizer?
Vamos discutir primeiro o “viés”. É fácil imaginar que, para ser capaz de prever com exatidão o futuro, primeiro é preciso entender bem o passado. Um preditor que não consegue mapear bem as características daquilo que já se observou claramente tende a não se sair bem para o futuro. O que aqui chamamos de “viés” são os desvios entre aquilo que se observou no passado e aquilo que se prevê pelo modelo proposto – em suma, é o quão bem o modelo está descrevendo os dados observados.
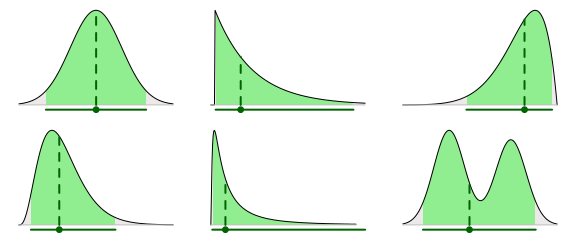
É natural pensar que quanto melhor o modelo descreve os dados da amostra, melhor ele é. Porém, isso não é verdade, pois o objetivo primordial não é descrever os dados, mas usá-los para fazer previsões (ou inferências) sobre o futuro. Isso nos leva para o lado da “variância”:
O objetivo aqui é conseguir prever a variável de interesse com base em alguns elementos. De cara temos um problema, pois aquilo que efetivamente vemos é apenas uma parte do fenômeno todo; então, se nos atermos demais a simplesmente descrever os dados disponíveis, estamos no fundo torcendo para que o mesmo padrão observado se repita para o futuro, o que claramente não é verdade. Para poder generalizar o que se observou para amostras futuras – ou seja, antecipar alguma coisa que ainda não aconteceu – é preciso calibrar o modelo de modo a capturar apenas o “essencial”, informações que realmente contribuem para uma boa previsão, em vez de captar por completo os padrões daquela amostra específica, pois ao fazer isso, informações inúteis (“ruído”) acabam sendo incorporadas ao mesmo tempo. Basicamente, ao forçar uma descrição muito fiel dos dados da amostra, acaba que se perde em capacidade de generalização, pois o futuro em geral não é uma extensão do passado.
Modelos que descrevem excessivamente bem os dados de uma amostra tendem a introduzir muita complexidade e volatilidade, de modo a prejudicar a capacidade de generalização. Na filosofia da ciência há um princípio chamado “navalha de Occam”, os estatísticos conhecem como “princípio da parcimônia”; a cultura popular adotou um mnemômico um tanto quanto ácido:
“KISS – keep it simple, stupid“
Basicamente, quer dizer que entre modelos com mesmo poder explicativo, o mais simples deles é o melhor, pois apresenta a mesma qualidade com um custo menor.
A essa altura, você já deve ter percebido que estamos diante de um cobertor curto, pois o cenário ideal que buscamos possui as duas características desejáveis, porém contraditórias: queremos um modelo que descreva bem os dados disponíveis E que seja capaz de generalizar para dados futuros. Se temos um modelo que se ajusta mal aos dados do passado (“under-fitting”), o modelo já começa com pouca confiabilidade, pois não está sendo fiel às informações disponíveis; por outro lado, um ajustamento excessivo (“over-fitting”) acaba assumindo que o futuro irá repetir o passado, de modo que o modelo tende a fornecer uma péssima previsão para observações que sejam apenas um pouquinho fora daquele padrão dos dados passados.
O dilema viés-variância é muito importante na construção de modelos matemáticos: a qualidade de um modelo depende diretamente das variáveis consideradas, e saber achar o meio-termo entre incorporar variáveis úteis e descartar variáveis inúteis pode ser um desafio e tanto. Vejamos um exemplo simplista: suponha que queremos construir um modelo para prever o preço de uma ação de uma empresa. É de se esperar que o desempenho econômico da empresa tenha uma influência decisiva no preço da ação, então podemos colocar como variáveis alguns indicadores como índice de lucratividade e liquidez, o market share da empresa, número de filiais, e por aí vai.
Poderíamos colocar por exemplo “escolaridade do CEO” como uma variável explicativa; é de se esperar que um gestor com uma formação acadêmica mais robusta possa incrementar o valor da companhia, mas a relação já não parece tão direta assim… Poderíamos colocar como variável se o CEO da empresa é destro, canhoto ou ambidestro, mas essa informação tende a não influenciar em nada na variável que se deseja prever, e a introdução dessa variável acabaria poluindo o modelo com uma complexidade desnecessária.
Note que não há limites para a criatividade do pesquisador, e teoricamente poderíamos colocar um número gigantesco de variáveis. Mas à medida que variáveis com menor relevância vão sendo inseridas, chega um momento em que a “variância” introduzida pela nova variável não compensa o poder explicativo que ela agrega ao modelo.
Saber encontrar o meio-termo ideal entre viés e variância não é uma tarefa fácil, há diversas técnicas para nos ajudar com isso, tais como validação cruzada e redução de dimensionalidade, podemos abordar esses tópicos em posts futuros.