Aprendizado Semi-Supervisionado para Detecção de Fraudes [Parte 2]
No post anterior, vimos o que é uma anomalia. Agora observaremos a forma de funcionamento de várias técnicas semi-supervisionadas para detecção de anomalia.
Os dados
Nós vamos utilizar a base de dados Credit Card Fraud Detection para demonstrar o funcionamento de várias técnicas semi-supervisionadas de detecção de anomalia. Segundo a descrição providenciada pelo fornecedor, “a base de dados contém transações feitas por cartão de crédito em setembro de 2013 por consumidores europeus. Os dados são de transações que ocorreram no período de dois dias, contando com 284’807 transações, dentre as quais 492 são fraudes. A base é altamente desbalanceada; o alvo positivo (fraude) corresponde a apenas 0,172% de todas as transações. Todos os dados são de variáveis numéricas, que são o resultado de transformação PCA, além de variáveis sobre o tempo em que a transação foi efetivada e sobre a quantidade transacionada”. Para efeito de esclarecimento, a técnica de PCA permite manter a informação integral dos dados ao mesmo tempo que retira sua interpretabilidade. Nesse caso, a técnica foi utilizada para manter o sigilo das informações bancárias.
Nós repartimos os dados em 3 subamostras. Em primeiro lugar, reservamos 80% das amostras de transações normais para treino, o que totalizou 227’452 observações. Essa sub amostra será nossa base de treinamento. Em seguida, nós separamos o restante das observações normais e anormais igualmente, formando duas sub amostras com 28’677 observações cada, sendo 246 dessas observações anômalas. A primeira dessas sub amostrar será nosso set de validação e será utilizada para ajustar o limiar da pontuação de anomalia, que será produzida pelo modelo treinado na primeira etapa. Por fim, a última subamostra será para testar a performance da técnica considerada.
Métricas de Avaliação
Em problemas de previsão, a métrica de avaliação mais comum é a acurácia, que mede a proporção de acertos. No entanto, nesse cenário, como mais de 99% dos dados pertencem a uma única categoria, um preditor ingênuo prevendo todas as observações como sendo normais já conseguiria mais de 99% de acerto. Isso nos motiva a utilizar outras métricas: precisão e revocação. Intuitivamente, um sistema com alta revocação e precisão baixa apontaria muitas observações como sendo anômalas, conseguindo achar a maior parte das anomalias, mas a um custo muito alto em falsos positivos. Por outro lado, um sistema com alta precisão e baixa revocação apontaria poucos resultados como sendo transações fraudulentas, acertando-as, porém a um custo de várias fraudes passarem despercebidas. Assim, um sistema ideal teria que ponderar precisão e revocação em algum ponto ótimo. Formalmente, tempos precisão e revocação definidos como:
\[P=\frac{T_p}{T+p + F_p} \quad \quad \quad R=\frac{T_p}{T+p + F_n}\]Em que \(T_p\) são os verdadeiros positivos, \(T_n\), os verdadeiros negativos, \(F_p\) são os falsos positivos e \(F_n\) são os falsos negativos.
Para que possamos comparar os modelos, é bom que tenhamos uma única métrica que resuma a performance. Para isso, vamos utilizar o \(F_2\)-score, que combina revocação e precisão, dando mais importância a primeira. Nós optamos por essa métrica porque acreditamos ser mais custoso não detectar uma fraude bancária que apontar uma transação como sendo fraudulenta e obter um alarme falso. Assim, desejamos que nosso sistema coloque mais importância em conseguir boa revocação. Formalmente, temos:
\[F_2-score = (1+2)^2 \ast \frac{P \ast R}{2^2 \ast P + R}\]Benchmark
A maioria dos bons trabalhos que utilizaram essa base de dados fizeram uso de aprendizado puramente supervisionado com alguma técnica para lidar com o desbalanceamento severo entre as categorias. Particularmente, este trabalho disponível no Kaggle conseguiu uma precisão de 0,883, uma revocação de 0,619 e um \(F_2\)-score de 0,658. Como esse é o melhor resultado que achamos dentre os trabalhos disponíveis no Kaggle, vamos tomá-lo como benchmark.
Técnicas de Detecção de Anomalias
Modelo Gaussiano
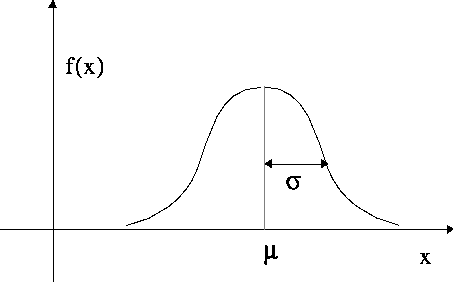
A distribuição gaussiana é dada pela curva em formato de sino (acima) e é, com certeza, o modelo estatístico mais famoso, principalmente porque muitos fenômenos do dia a dia se encaixam muito bem nela. Intuitivamente, se um fenômeno tem comportamento gaussiano, podemos dizer que 95% das realizações desse fenômeno aconteceram a no máximo 2 desvios padrões de distância da média. Por exemplo, se a quantidade média transacionada por cartão de crédito for de R$ 50,00, com um desvio padrão de R$ 10,00, podemos dizer que 95% das transações serão de um valor entre 30 e 70 reais. Mais ainda, nós podemos dizer que transações fora desse intervalo são bastante improváveis, indicando que podem ser anomalias. Aqui, nós estendemos a distribuição gaussiana para o seu caso multivariado, para assim capturar interações entre variáveis. Por exemplo, pode ser que uma grande quantia transacionada por si só não seja estranha, mas essa mesma quantia em uma especifica hora do dia, digamos de madrugada, seja. Nós podemos então modelar as margens da normalidade pela interação entre hora do dia e quantidade transacionada.
Nossos dados contêm 30 variáveis, logo não podemos visualizá-los em um gráfico como o acima. No entanto, achar uma gaussiana de 30 dimensões é tão simples quanto achar uma de duas e é isso que fizemos com os nossos dados de treino, isto é, a subamostra não nomeada. Quando encontramos a gaussiana multidimensional que melhor se encaixa nos dados, nós podemos extrair a probabilidade de cada observação, que seria a altura da gaussiana multidimensional. Em seguida, nós usamos a subamostra (nomeada) de validação para ajustar um limiar a partir do qual consideraríamos uma transação como anômala. Apenas para efeito de clarificação, ao invés de usar a probabilidade para decidir o limiar, nós usamos o logaritmo da probabilidade (fizemos isso pois a probabilidade é um número muito pequeno que poderia dar problemas de precisão numérica, devido a capacidade limitada do computador em representar números com muitas casas decimais). Abaixo, vemos como as nossas três métricas de avaliação evoluem conforme mudamos o limiar.
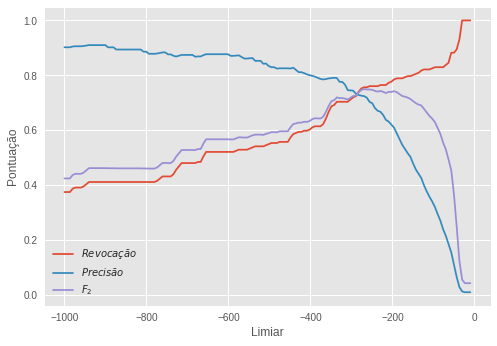
O limiar ótimo escolhido foi de -269, isto é, amostras com uma log probabilidade menor do que essa serão consideradas anomalias pelo nosso modelo. Com essa regra aprendida, nós criamos a subamostra de teste para uma avaliação final. As pontuações nessa subamostra foram:
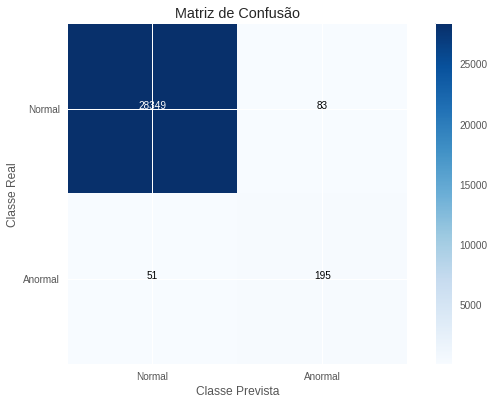
\[R=0,793 \quad P=0,701 \quad F_2=0,773\]Apenas para que fique claro, uma revocação de 0,793 indica que, de todas as transações fraudulentas, nós conseguimos identificar 79,3% delas; uma precisão de 0,701 indica que, de todas as transações que previmos como sendo fraudulentas, 70,1% delas de fato o eram. O \(F_2\)-score não tem nenhuma interpretação intuitiva. Ele é apenas uma métrica que combina as outras duas de forma que possamos comparar os modelos mais facilmente. Por exemplo, podemos dizer que esse modelo é mais de 10 pontos melhor do que o nosso benchmark, que obteve um \(F_2\)-score de apenas 0,658. Abaixo está a matriz de confusão para mais detalhes sobre como o modelo classificou cada transação.
Modelo Histograma
Nem todas as variáveis dos nossos dados seguem uma distribuição gaussiana. Se plotarmos o histograma de algumas características, podemos ver isso claramente. A começar pela distribuição da variável que mede a quantidade transacionada, que tem uma distribuição bastante complicada, tanto para os dados normais quanto para os anormais. (Novamente, para efeito de esclarecimento, transformamos a variável de quantidade transacionada em sua forma logarítmica. Isso costuma deixar as distribuições mais balanceadas).
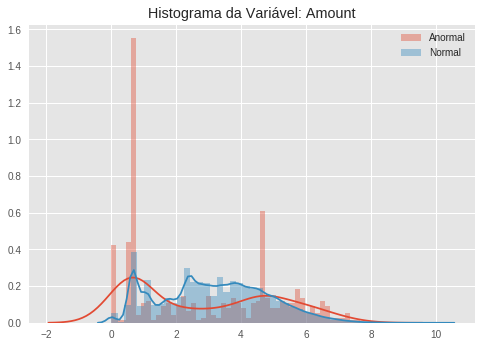
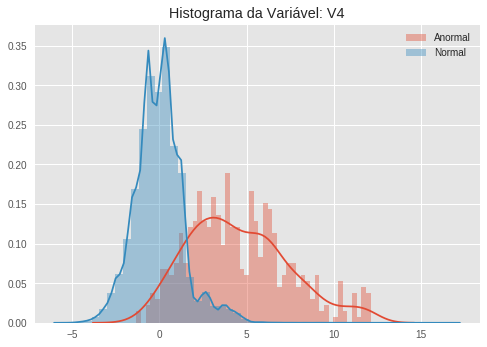
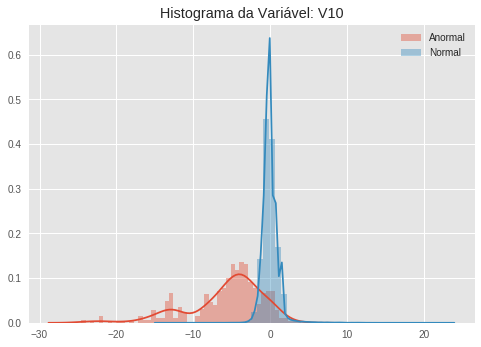
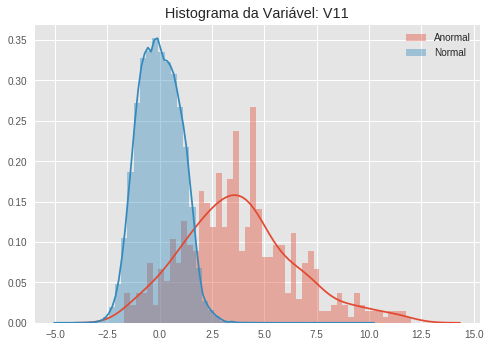
Quando vemos esses histogramas, notamos facilmente como algumas variáveis são ótimos indicadores de anomalias, uma vez que a distribuição (aproximada pelo histograma) dos dados anômalos e dos dados normais são bastante distinguíveis. Veja por exemplo a variável V10. A distribuição dos dados normais parece uma gaussiana bastante concentrada no zero, ao passo que os dados anormais parecem seguir uma distribuição bimodal, com um pico em aproximadamente -5 e outro em -15.
Nós vamos explorar essa diferença nos histogramas para construir uma pontuação de normalidade que será proporcional à probabilidade dos dados corresponderem a uma transação normal. Em primeiro lugar, vamos usar os dados de treinamento (não nomeados e com exemplos apenas dos casos normais) para estimar um histograma para cada variável nos dados. Assim, na hora de avaliar uma nova observação, nós analisamos em qual dos compartimentos dos histogramas cada uma de suas variáveis cai. A pontuação de normalidade será então a média da altura desses compartimentos. É fácil perceber que se a observação for normal, ela cairá em uma região do histograma com compartimentos bastante altos.
Uma vez treinado esse modelo, vamos ajustar o limiar para essa nossa pontuação usando a subamostra de validação, que inclui dados nomeados, tanto do caso normal quanto do caso anormal.
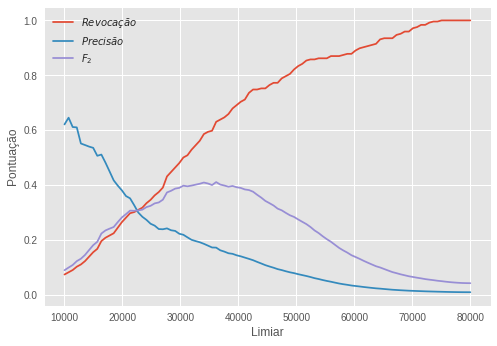
O melhor limiar, de acordo com o \(F_2\)-score, foi 36161. Com o modelo assim ajustado, conseguimos os seguintes resultados:
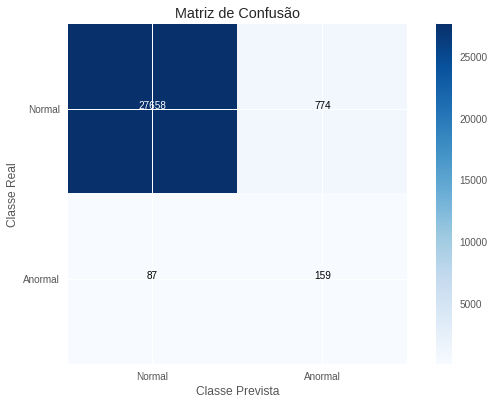
\[R=0,646 \quad P=0,170 \quad F_2=0,415\]Observamos que esse modelo não é melhor que nosso benchmark, conseguindo um \(F_2\)-score de apenas 0,41. A performance do modelo é particularmente prejudicada pela baixa precisão, de 0,17. Isso indica que, de todas as observações que esse modelo classifica como sendo fraudulentas, apenas 17% delas de fato o são. Assim, o modelo incorre a um elevado custo em termos de falsos positivos. Devemos notar que esse modelo é capaz de aproximar qualquer distribuição por variável, mas não consegue capturar relações entre variáveis. Aparentemente, conseguir capturar interações é algo bastante importante nos dados aqui presente. Abaixo, na matriz de confusão, temos uma ideia melhor do tipo de erro que estamos cometendo.
Modelo de Mistura de Gaussianas
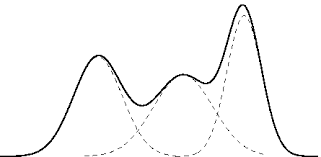
Anteriormente, no modelo gaussiano nós assumimos que os dados vinham de uma distribuição gaussiana multidimensional. Isso talvez seja um pouco restritivo. Como vimos nos histogramas acima, nem todas as variáveis seguem um modelo gaussiano. Nós podemos utilizar um modelo que relaxa essa hipótese, assumindo que os dados vêm de uma distribuição que é uma mistura de gaussianas. Pela imagem acima, observamos que essa hipótese não é nem um pouco restritiva e que distribuições bastante complexas podem ser representadas por misturas de gaussianas. De fato, contanto que tenhamos gaussianas suficiente, qualquer distribuição poderá ser aproximada por uma mistura de gaussiana.
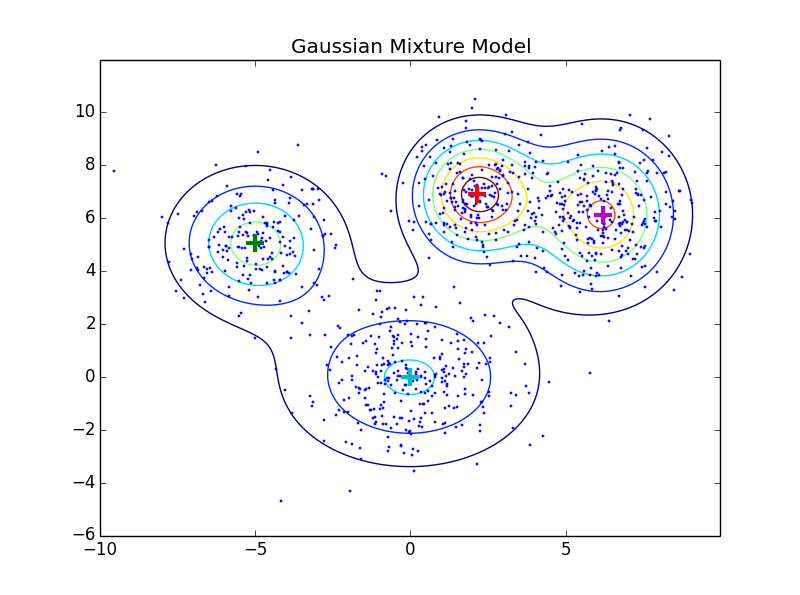
Se quisermos capturar interações entre variáveis, é fácil o suficiente estender o modelo para uma mistura de gaussianas multivariadas, como na imagem abaixo (dimensão da probabilidade/altura está suprimida e representada como curva de nível):
No nosso modelo de detecção de anomalias, nós ajustamos 3 gaussianas aos dados com um algoritmo de Expectativa-Maximização. Fizemos isso utilizando apenas os dados de treino, que não estavam nomeados e que continham apenas casos de transações normais. Com esse modelo treinado, conseguimos mais uma vez ter acesso direto à probabilidade de cada amostra e mais uma vez optamos por utilizar o logaritmo da probabilidade para não ter que lidar com muitas casas decimais. Na subamostra de validação com dados nomeados, ajustamos um limiar para o logaritmo da probabilidade, para decidir abaixo de que pontuação consideraríamos uma anomalia. A evolução das três métricas conforme a evolução do limiar pode ser conferida abaixo.
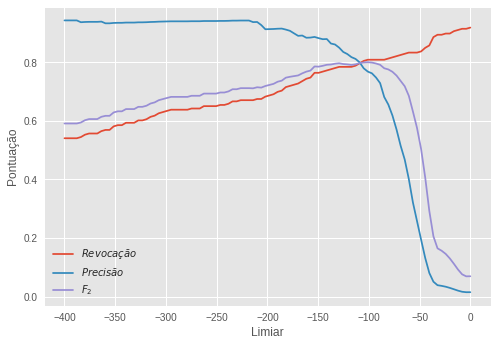
O limiar ótimo escolhido foi de -101, de forma que observações com uma pontuação menor do que isso seriam consideradas anômalas. Por fim, tornamos à subamostra de teste para uma avaliação final. Os resultados foram os seguintes:
\[R=0,809 \quad P=0,726 \quad F_2=0,791\]Esse foi o nosso melhor modelo, com elevada revocação e precisão. Para mais informações sobre o tipo de erro que esse modelo comete, abaixo colocamos a matriz de confusão da avaliação final, na subamostra de teste.
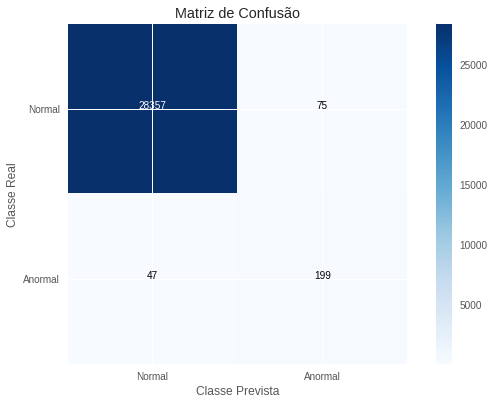
No post 3 analisaremos mais algumas técnicas de detecção de anomalia. Parte 3 - Final