Tutorial de SVM
Neste tutorial será trabalhado uma introdução geral a Support Vector Machines (SVM) e uma aplicação básica utilizando o pacote e1071.
O que é o Support Vector Machine?
O Support Vector Machine, também conhecido como Máquina de Suporte Vetorial, foi elaborado com o estudo proposto por Boser, Guyon e Vapnik em 1992. Ele é um algoritmo de aprendizado supervisionado, cujo objetivo é classificar determinado conjunto de pontos de dados que são mapeados para um espaço de características multidimensional usando uma função kernel, abordagem utilizada para classificar problemas. Nela, o limite de decisão no espaço de entrada é representado por um hiperplano em dimensão superior no espaço (VAPNIK et al., 1997 e SARADHI et al., 2005).
De forma mais simples…
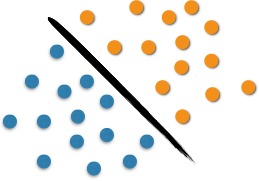
O SVM realiza a separação de um conjunto de objetos com diferentes classes, ou seja, utiliza o conceito de planos de decisão. Podemos analisar o uso do SVM com o seguinte exemplo. Na Figura 1 é possível observar duas classes de objetos: azul ou laranja. Essa linha que os separa define o limite em que se encontram os pontos azuis e os pontos laranjas. Ao entrarem novos objetos na análise, estes serão classificados como laranjas se estiverem à direita e como azuis caso situem-se à esquerda. Neste caso, conseguimos separar, por meio de uma linha, o conjunto de objetos em seu respectivo grupo, o que caracteriza um classificador linear.
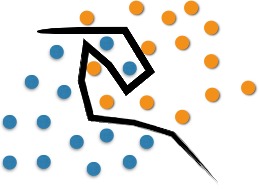
No entanto, problemas de classificação costumam ser mais elaborados, sendo necessário realizar a separação ótima por meio de estruturas mais complexas. O SVM propõe a classificação de novos objetos (teste) com base em dados disponíveis (treinamento). Como pode-se observar na Figura 2. A separação ótima nesse caso ocorreria com a utilização de uma curva.
Na esquerda da Figura 3 observamos a complexidade em separar os objetos originais. Para mapeá-los, utilizamos um conjunto de funções matemáticas, conhecido como Kernels. Esse mapeamento é conhecido como o processo de reorganização dos objetos.
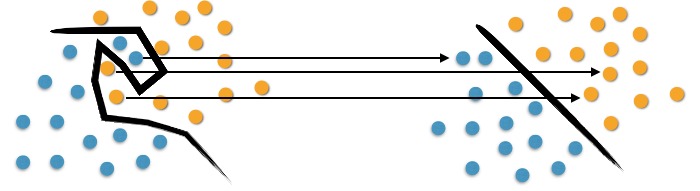
Observa-se que à direita da Figura 3 há uma separação linear dos objetos. Assim, ao invés de construir uma curva complexa, como no esquema à esquerda; o SVM propõe, nesse caso, essa linha ótima capaz de separar os pontos azuis dos laranjas.
E agora, como posso aplicar esse modelo?
Primeiramente, é necessário carregar os dados que serão estudados. Felizmente esse dataset já está disponível nativamente no R. Para carregá-lo, basta executar o seguinte comando:
data(iris)
Após carregar a base algumas explorações serão feitas:
summary(iris)
head(iris)
tail(iris)
str(iris)
O comando summary apresenta algumas estatísticas das variáveis do dataframe, como média, mediana, máximo, mínimo e quantis.
>summary(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 setosa :50
1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 versicolor:50
Median :5.800 Median :3.000 Median :4.350 Median :1.300 virginica :50
Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
Os comandos head e tail mostram as primeiras seis linhas e as últimas seis linhas nesta ordem. Já o comando str apresenta a estrutura das variáveis. Por exemplo, se são quantitativas ou categóricas.
> head()
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
A partir disso, é possível ter uma noção de como são os dados e quais os tipos de variáveis trabalhadas. É muito importante conhecer bem os dados que serão usados.
Como vamos utilizar as variáveis quantitativas ‘Sepal Length’, ‘Sepal Width’, ‘Petal Length’ e ‘Petal Width’ como preditoras para a variável categórica ‘Species’, é interessante observar a correlação entre as covariáveis do modelo.
> names(iris)
[1] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width" "Species"
> cor(iris[,1:4])
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 1.0000000 -0.1175698 0.8717538 0.8179411
Sepal.Width -0.1175698 1.0000000 -0.4284401 -0.3661259
Petal.Length 0.8717538 -0.4284401 1.0000000 0.9628654
Petal.Width 0.8179411 -0.3661259 0.9628654 1.0000000
Gráficos contam histórias!
Gráficos são uma excelente ferramenta de abstração e apresentação de suas explorações, estudos que atingem maior público são aqueles que usam de todos os recursos póssiveis para tornar a informação o mais inteligivel possivel, vamos visualizar como cada variável se relaciona por um mapa de gradiente, definindo o vermelho (cor quente) para maior correlação entre as variáveis e o azul (cor fria) para menor correlação:
library(lattice)
cor <- cor(iris[,1:4])
rgb.palette <- colorRampPalette(c("blue", "red"), space = "rgb")
levelplot(cor, main="Correlation Iris Dataset", xlab="", ylab="", col.regions=rgb.palette(120))
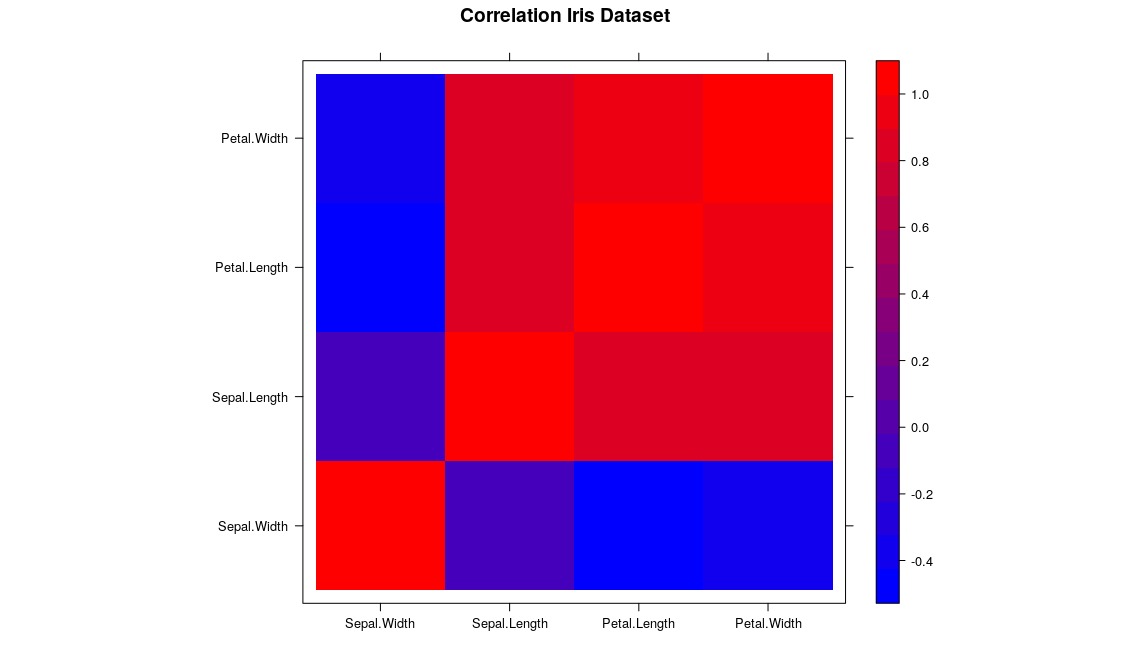
Um belo gráfico de correlação. ![]() Primeiro importamos a biblioteca
Primeiro importamos a biblioteca lattice responsável pela geração de nosso gráfico, armazenamos a matriz de correlação em uma variável e então criamos uma paleta de cores (um array com a definição computacional dessas cores) com a função colorRampPaletter, indo do azul ao vermelho, por fim passamos essas definições a função levelplot que cuidará do resto.
Agora o gráfico definitivo para entendermos os nossos dados, o gráfico de dispersão tridimensional. Temos quatro variáveis mas apenas 3 nos possibilitarão enxergar além!
install.packages("scatterplot3d")
library(scatterplot3d)
colors <- c("#e41a1c", "#377eb8", "#4daf4a")
colors <- colors[as.numeric(iris$Species)]
scatterplot3d(iris[,1:3], pch = 15, color=colors)
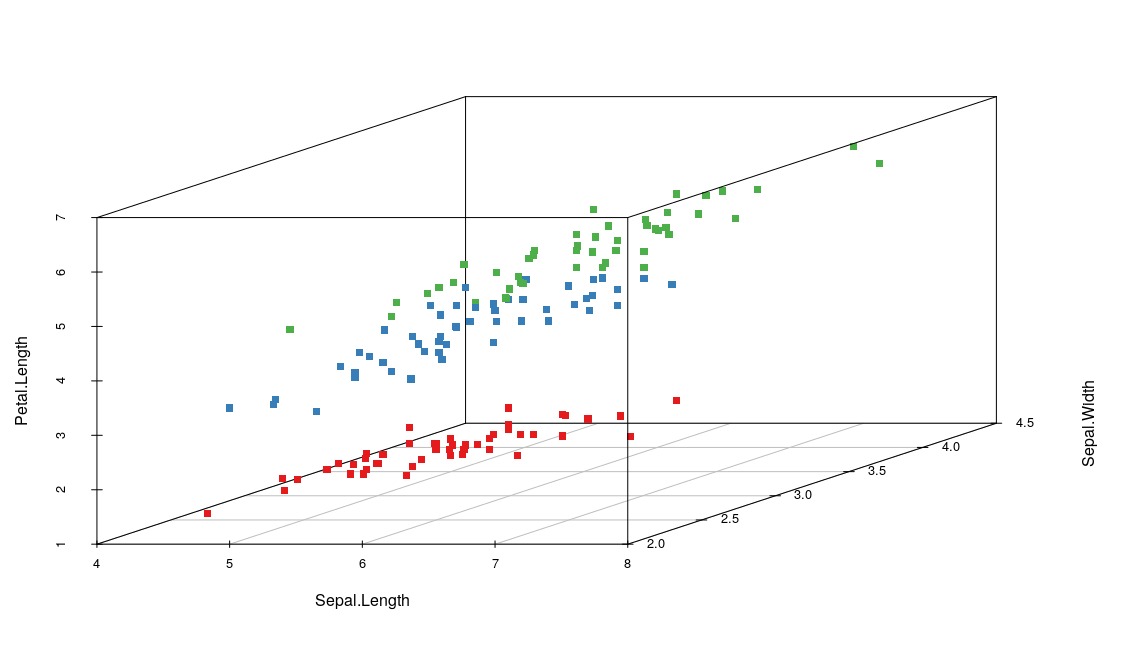
Com o pacote scatterplot3d instalado e carregado, definimos 3 cores hexadecimais e salvamos no array colors, então sobrescrevemos esse array com um array referente a espécie substituindo pela cor, especie 1, cor 1, especie 2, cor 2… Por fim passamos todos esses parametros para nossa função que gera nosso gráfico. Como pode ver é clara uma ‘separação’ para os nossos dados, assim não será um trabalho difícil para nossa máquina.
Agora a parte mais esperada… #vamoslá
Para utilizar o SVM, é necessário instalar o pacote e1071 por meio do comando install.packages("e1071").
Aguarde o processo de instalação finalizar e vamos à separação dos dados.
Primeiramente, iremos separar 70% das observações do dataset para ‘calibrarmos’ o modelo e utilizaremos as demais observações para verificar o poder de predição do modelo ajustado.
> dim(iris)
[1] 150 5
> treino <- sample(1:150, 0.7*150)
> teste <- setdiff(1:150,treino)
> iris_treino <- iris[treino,]
> iris_teste <- iris[teste,]
No pacote e1071, usamos a função svm() para ajustar o modelo de máquina de suporte vetorial. Nota-se que a sintaxe é bastante parecida com as funções lm() e glm() para modelos, lineares e lineares generalizados. Uma vez que declaramos a variável dependente (a variável em que queremos fazer predições), a função automaticamente detecta o seu tipo (categórica ou quantitativa) e utiliza o procedimento adequado para o ajuste do modelo.
> require(e1071)
> modelo1 <- svm(Species ~ . , data = iris_treino)
> summary(modelo1)
Call:
svm(formula = Species ~ ., data = iris_treino)
Parameters:
SVM-Type: C-classification
SVM-Kernel: radial
cost: 1
gamma: 0.25
Number of Support Vectors: 49
Vimos que foi utilizado o kernel “radial” no modelo proposto, pois é o default (o que a função admite se nada é informado no argumento). A função svm() aceita os seguintes kernels: radial, linear, polynomial e sigmoide.
Diferentes kernels ajustam diferentes modelos e, consequentemente, diferentes valores preditos. Ajustaremos então, um modelo para cada kernel, visando obter uma menor taxa de erro de classificação.
modelo2 <- svm(Species ~ . , kernel = "linear" , data = iris_treino)
modelo3 <- svm(Species ~ . , kernel = "polynomial" , data = iris_treino)
modelo4 <- svm(Species ~ . , kernel = "sigmoid" , data = iris_treino)
Agora aplicamos os modelos ajustados nas observações da base ‘teste’ e, por meio de uma tabela de contingência, comparamos a classificação proposta pelos modelos com a classificação real das observações.
preditos1 <- predict(modelo1,iris_teste)
> table(preditos1,iris_teste$Species)
preditos setosa versicolor virginica
setosa 11 0 0
versicolor 0 20 0
virginica 0 1 13
Ao realizar o mesmo procedimento para os demais modelos, podemos utilizar a soma dos elementos não pertencentes à diagonal principal como uma medida de erro, já que estes correspodem aos elementos classificados erroneamente.
preditos2 <- predict(modelo2,iris_teste)
preditos3 <- predict(modelo3,iris_teste)
preditos4 <- predict(modelo4,iris_teste)
t1 <- table(preditos1,iris_teste$Species)
t2 <- table(preditos2,iris_teste$Species)
t3 <- table(preditos3,iris_teste$Species)
t4 <- table(preditos4,iris_teste$Species)
> sum(c(t1[lower.tri(t1)],t1[upper.tri(t1)]))
[1] 1
> sum(c(t2[lower.tri(t2)],t2[upper.tri(t2)]))
[1] 1
> sum(c(t3[lower.tri(t3)],t3[upper.tri(t3)]))
[1] 3
> sum(c(t4[lower.tri(t4)],t4[upper.tri(t4)]))
[1] 7
Assim, vimos que o modelo1 (kernel = radial) e o modelo2 (kernel = linear) apresentaram resultados mais satisfatórios, pois erraram apenas uma classificação na base de teste.
Conclusão
O SVM possui grande abrangência de aplicações em diversas áreas, como finanças, biologia, medicina, logística, entre outras. Isso ocorre devido às suas vantagens de aplicação como: bom desempenho de generalização; tratabilidade matemática; interpretação geométrica e a utilização para a exploração de dados não rotulados (YANG et al., 2002). Este tutorial é apenas uma pequena demonstração de como esta poderosa ferramenta pode ser utilizada. Esperamos que tenha sido útil para os nossos leitores!
Referências
BOSER, B. E.; GUYON, I. M.; VAPNIK, V. N. A Training Algorithm for Optimal Margin Classifiers. In: ANNUAL WORKSHOP ON COMPUTACIONAL LEARNING, 5, 1992, Pittsburgh. ACM Press. Pittsburgh: Haussler D, jul 1992. p.144-152 .
DRUCKER, H.; BURGES, C. J.; KAUFMAN, L.; SMOLA, A.; VAPNIK, V. Support vector regression machines. Advances in neural information processing systems, Morgan Kaufmann Publishers, p. 155–161, 1997.
SARADHI, V., KAMIK, H., MITRA, P. A Decomposition Method for Support Vector Clustering. In Proc. of the 2nd International Conference on Intelligent Sensing and Information Processing (ICISIP), p. 268-271, 2005.