Introdução básica à Clusterização
O que é Clusterização?
Clusterização é o agrupamento automático de instâncias similares, uma classificação não-supervisionada dos dados (esse termo não é familiar? Veja nosso post sobre os três tipos de aprendizado de máquina!). Ou seja, um algoritmo que clusteriza dados classifica eles em conjuntos de dados que ‘se assemelham’ de alguma forma - independentemente de classes predefinidas. Os grupos gerados por essa classificação são chamados clusters.
Uma forma de clusterização seria, por exemplo, a partir de dados de animais em um zoológico aproximar animais por suas características. Ou seja, a partir dos dados como ‘quantidade de pernas’, ‘quantidade de dentes’, ‘põe ovo’, ‘tem pêlos’ e vários outros, procuramos animais que estão mais próximos. Poderíamos assim clusterizar os dados, separar animais em mamíferos, aves ou répteis mas sem “contar” ao algoritmo sobre estas classificações. Apenas comparando a distância entre dados o algoritmo mostraria que um tigre está “mais próximo” de um leão do que de uma garça.
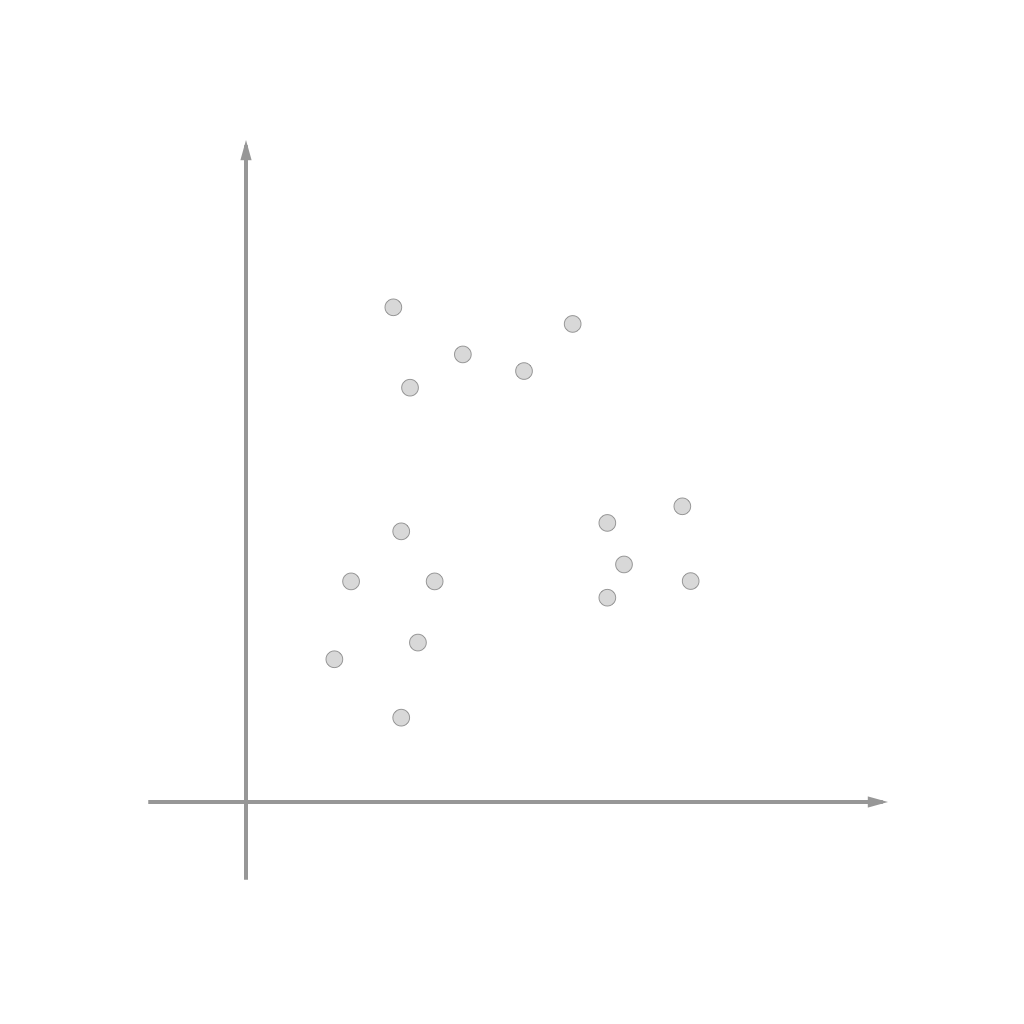
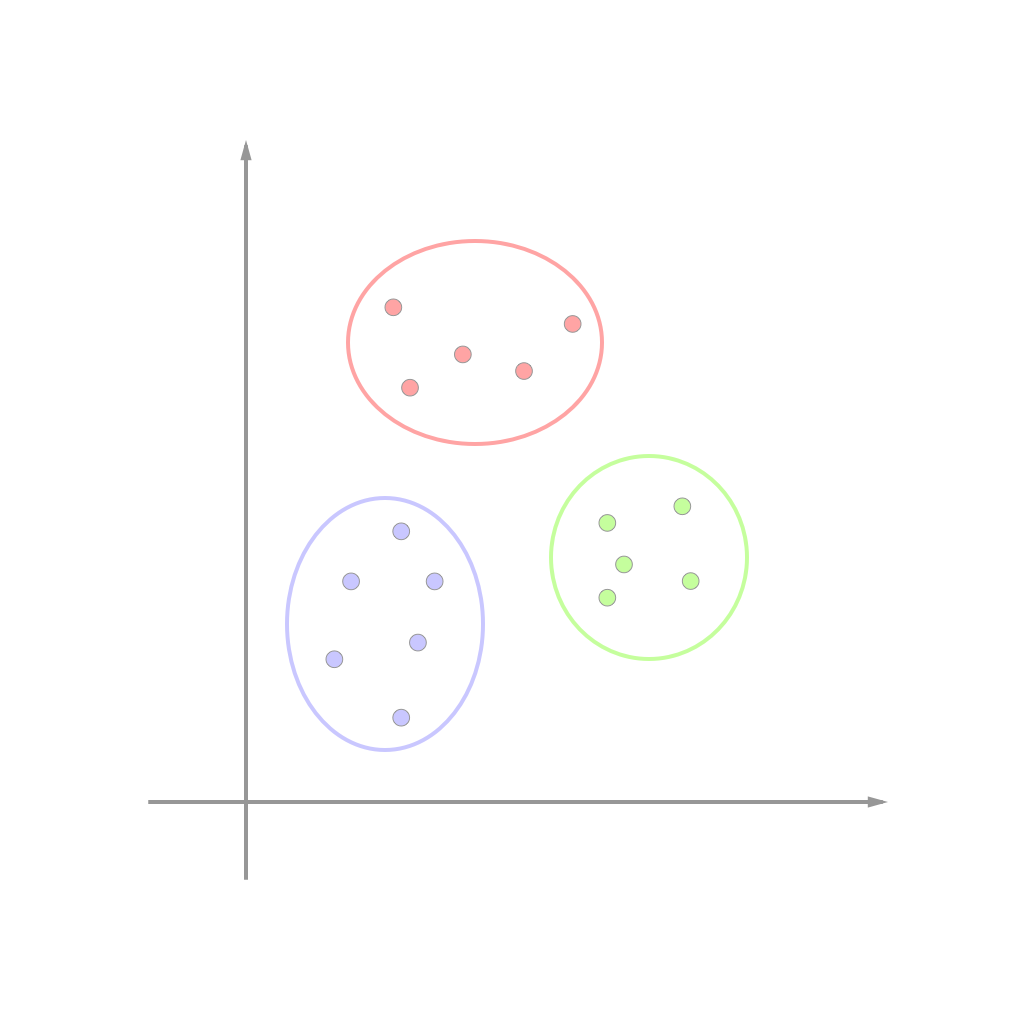
As imagens a seguir ilustram uma clusterização bem simples de dados com apenas duas dimensões (duas “características”):
| Dados | Dados agrupados em clusters |
|---|---|
 |
 |
Muitas vezes, a similaridade entre os dados é encontrada por métricas de distância. Um dos algoritmos mais básicos para Clusterização chama-se K-Means.
K-Means
O algoritmo se chama assim pois encontra k clusters diferentes no conjunto de dados. O centro de cada cluster será chamado centróide e terá a média dos valores neste cluster.
A tarefa do algoritmo é encontrar o centróide mais próximo (por meio de alguma métrica de distância) e atribuir o ponto encontrado a esse cluster. Após este passo, os centróides são atualizados sempre tomando o valor médio de todos os pontos naquele cluster. Para este método são necessários valores numéricos para o cálculo da distância, os valores nominais então podem ser mapeados em valores binários para o mesmo cálculo. Em caso de sucesso, os dados são separados organicamente podendo assim ser rotulados e centróides viram referência para classificar novos dados.
Para o exemplo utilizaremos o Iris Data Set do UCI Machine Learning Repository. Este é um dos conjuntos de dados mais conhecidos e utilizados para exemplos simples de reconhecimento de padrões. O conjunto de dados contém 3 classes de 50 instâncias cada, onde cada classe se refere a um tipo de planta Iris.
Passo a passo do algoritmo
O Κ-means aprimora de forma iterativa seus resultados até alcançar um resultado final. O algoritmo recebe o número de clusters Κ e o conjunto de dados a ser analisado. Em seguida são estabelecidas posições iniciais para os K centróides, que podem ser gerados ou selecionados aleatoriamente dentro do conjunto de dados.
O algoritmo é iterado nos seguintes passos até que se estabilize:
-
Associação de cada instância a um centróide - cada centróide define um cluster, então cada instância será associada a seu cluster mais semelhante (centróide mais próximo). A distância será calculada por alguma métrica de distância, em geral utiliza-se a distância euclidiana entre as duas instâncias;
-
Atualização dos centróides - centróides dos clusters são recalculados, a partir da média entre todas as instâncias associadas àquele cluster.
Na prática com Python
Para que possamos testar o algoritmo utilizaremos a linguagem Python e algumas de suas bibliotecas
- Se você ainda não tem Python em sua máquina, dê uma olhada no nosso post Instalando Python para Aprendizado de Máquina;
- Crie um diretório de trabalho em sua máquina, uma pasta que conterá seu programa e os dados utilizados. Decidi chamar meu diretório de ‘learn-clustering’;
- Faça download do iris.data no seu novo diretório;
- Crie um novo arquivo python onde escreveremos nosso programa no mesmo diretório principal ou um Jupyter Notebook. Os trechos de código a seguir devem ser codificados dentro do arquivo criado.
1. Importando as pacotes
Usaremos:
- NumPy (pacote básico para computação científica e matemática, com diversas funções e operações sofisticadas)
- Pandas (pacote para manipulação e estruturação de dados)
- Matplotlib (pacote para plotagens gráficas em 2D)
- sklearn (pacote de Machine Learning contendo a ferramento do algoritmo KMeans pronta)
import numpy as np # 1
import pandas as pd # 2
import matplotlib.pyplot as plt # 3
from sklearn.cluster import KMeans # 4
2. Lendo o Dataset
A leitura dos dados é feita a partir da biblioteca Pandas e os dados estão organizados no formato csv (comma-separated values) apesar da extensão ‘.data’. Chamaremos o dataset completo de dataset. Os atributos têm seus nomes indicados nos dados, utilizaremos o array ‘headers’ para nomeá-las de acordo com a documentação do conjunto de dados.
headers = ['sepal length', 'sepal width', 'petal length', 'petal width', 'class']
dataset = pd.read_csv("./iris.data", encoding = "ISO-8859-1", decimal=",", header=None, names=headers)
A variável ‘dataset’ recebe os dados lidos, ‘header=None’ indica que os dados no têm cabeçalho e ‘names=headers’ faz com que os cabeçalhos deste dataset sejam os definidos na variável ‘headers’
Trecho do Dataset:
| sepal length | sepal width | petal length | petal width | class |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | Iris-setosa |
| 4.9 | 3.0 | 1.4 | 0.2 | Iris-setosa |
| 4.7 | 3.2 | 1.3 | 0.2 | Iris-setosa |
| … | … | … | … | … |
| 7.0 | 3.2 | 4.7 | 1.4 | Iris-versicolor |
| 6.4 | 3.2 | 4.5 | 1.5 | Iris-versicolor |
| 6.9 | 3.1 | 4.9 | 1.5 | Iris-versicolor |
| … | … | … | … | … |
| 6.3 | 3.3 | 6.0 | 2.5 | Iris-virginica |
| 5.8 | 2.7 | 5.1 | 1.9 | Iris-virginica |
| 7.1 | 3.0 | 5.9 | 2.1 | Iris-virginica |
Podemos perceber que cada coluna é referente uma característica daquele espécime de planta. Ou seja, cada caso específico de flor produz uma instância diferente, que têm dados próprios.
3. Pré-processando os dados
Para garantirmos dados numéricos, vamos garantir que as colunas sejam do tipo float:
for col in dataset.columns[0:4]:
dataset[col] = dataset[col].astype(float)
Podemos confirmar os tipos de cada coluna do dataset com o ‘dtypes’
dataset.dtypes
sepal length float64
sepal width float64
petal length float64
petal width float64
class object
dtype: object
Agora deve ser realizada a divisão dos dados entre variáveis dependentes ( X ) e independente ( y ). Uma definição de variáveis dependentes e independentes pode ser encontrada no nosso post Os Três Tipos de Aprendizado de Máquina
X = dataset.iloc[:, 0:4]
y = dataset.iloc[:, 4]
Agora vamos aplicar o kmeans no conjunto de variáveis dependentes - ou seja, não estamos ‘contando’ ao algoritmo quais são as classes de cada instância de flor, estamos apenas apresentando os dados que cada instância tem. Definimos o número de clusters - k - como 3, uma situação ideal. Existem técnicas para encontrar o melhor k que serão abordadadas em um próximo post.
kmeans = KMeans(n_clusters=3, random_state=0).fit(X)
X_clustered = kmeans.fit_predict(X)
Existem várias formas de checar a clusterização realizada, uma bem simples é criando uma tabela de resultados contendo a coluna das classes esperadas e a coluna dos clusters criados:
results = dataset[['class']].copy()
results['clusterNumber'] = X_clustered
results
Tabela ‘results’
| class | clusterNumber |
|---|---|
| Iris-setosa | 0 |
| Iris-setosa | 0 |
| Iris-setosa | 0 |
| … | … |
| Iris-versicolor | 1 |
| Iris-versicolor | 1 |
| Iris-versicolor | 1 |
| … | … |
| Iris-virginica | 2 |
| Iris-virginica | 2 |
| Iris-virginica | 2 |
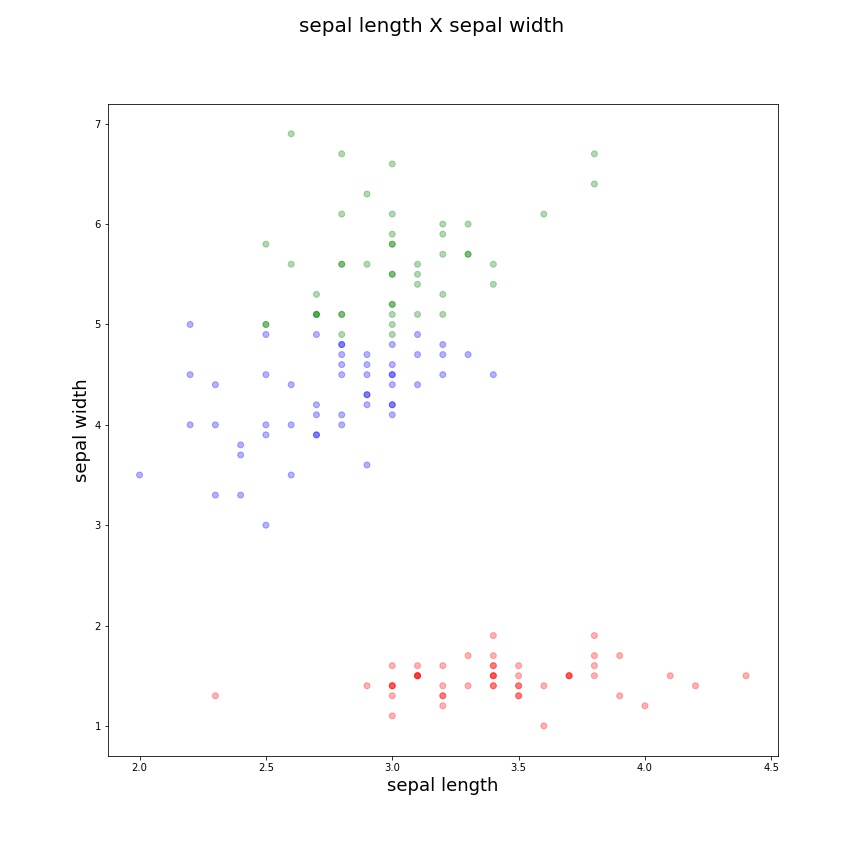
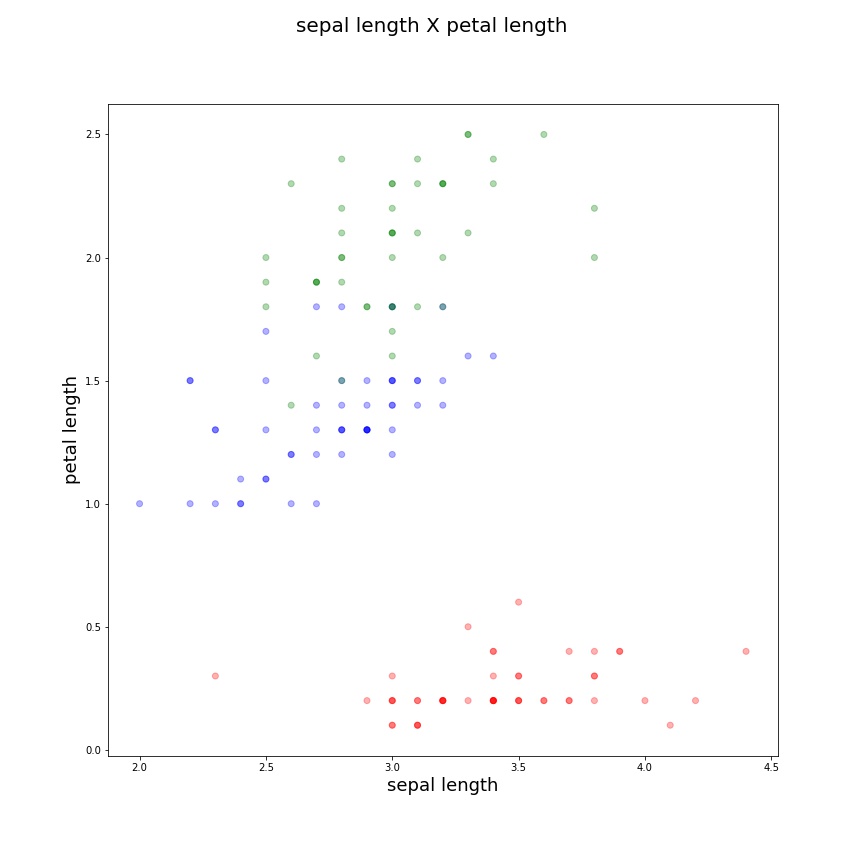
Neste pequeno dataset é simples visualizar que atingimos a clusterização esperada. Podemos agora testar uma abordagem mais gráfica. Primeiramente vamos definir cores para os diferentes tipos de clusters e ‘pintar’ pontos em clusteres diferentes de cores diferentes:
LABEL_COLOR_MAP = {0 : 'red', 1 : 'blue', 2: 'green'}
label_color = [LABEL_COLOR_MAP[l] for l in X_clustered]
Agora podemos plotar um gráfico que compare duas características em duas dimensões. A lógica a seguir é apenas para que possamos plotar dinamicamente mudando apenas os valores de ‘c1’ e ‘c2’ que serão características diferentes a serem comparadas e dispostas nos eixos do gráfico.
c1 = 0 # valor do índice da coluna, pode ser 0, 1 ou 2
c2 = 1
labels = ['sepal length', 'sepal width', 'petal length']
c1label = labels[c1]
c2label = labels[c12]
title = xlabel + ' x ' + ylabel
Com as características escolhidas, plotamos o gráfico com Matplotlib:
plt.figure(figsize = (12,12))
plt.scatter(X.iloc[:, c1],X.iloc[:, c2], c=label_color, alpha=0.3)
plt.xlabel(c1label, fontsize=18)
plt.ylabel(c2label, fontsize=18)
plt.suptitle(title, fontsize=20)
plt.savefig(title + '.jpg')
plt.show()
| sepal length X sepal width | sepal length X petal length | sepal width X petal length |
|---|---|---|
 |
 |
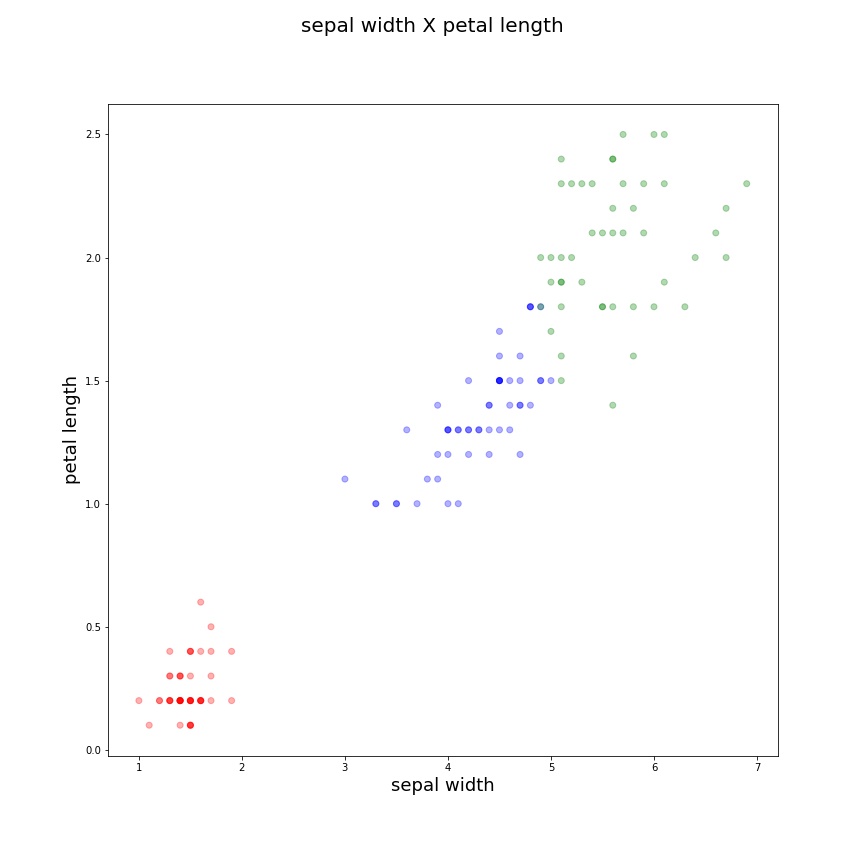 |
E como podemos ter uma noção da qualidade dos nossos clusters encontrados? A forma mais simples de verificarmos a “qualidade” dos clusters encontrados é medindo os valores inter-clusters e intra-clusters.
-
A distância inter-clusters (entre clusters) nos diz o quão distantes estão os clusters dos outros, ou seja, em geral é um bom sinal quando eles estão distantes entre si pois mostram maior isolamento dos grupos e provavelmente uma classificação mais precisa.
-
A distância intra-cluster (interna aos clusters) nos diz o quão distantes estão os elementos de um mesmo grupo e o quão distantes estão de seu centróide, ou seja, em geral grupos mais densos com elementos mais próximos têm maior similaridade e tem mais chance de realmente compartilharem a mesma classificação
De uma forma bem simplista, podemos dizer que alcançamos clusters interessantes quando eles se isolam do resto e têm uma “alta densidade”, seus elementos são mais próximos. Naturalmente isto serve apenas para uma análise simples, existem várias técnicas mais avançadas de validação da clusterização que abordaremos em um post futuro.
Neste exemplo fica clara a divisão entre classes diferentes, assim podemos compreender como a clusterização funciona e que existem casos específicos em que a técnica será muito útil. Aplicações possíveis da clusterização incluem:
- Marketing: Pesquisa e segmentação de mercado para determinar potenciais grupos homogêneos de consumidores para melhor definir a disposição de produtos que uma estratégia corporativa;
- Análise de redes sociais: Dentro de um grande grupo de pesoas, reconhecer comunidades que compartilhem de alguma preferência ou opinião;
- Reconhecimento de imagens: Clusterização pode ser aplicado para se reconhecer uma pessoa ou um objeto numa foto; os clusters seriam as regiões da imagem que contenham rostos, paisagem, vestimentas, etc.;
- Detecção de anomalias: A análise de clusters pode ser adaptada para a detecção de outliers que destoem da maioria dos outros elementos baseada em alguma métrica de similaridade;
- Finanças: clusterização pode ser utilizado para agrupar empresas por similaridade, o que pode ser bem útil para a construção de portfólios, cuja teoria clássica preconiza que o risco do investidor pode ser diversificado quando se aplica em empresas pouco correlacionadas. A clusterização ainda pode ser usada para a identificação de períodos de alta e baixa volatilidade, o que por sua vez pode subsidiar a construção de estratégias de trading e de gestão do risco.
Nem todo resultado terão dados ideais como este conjunto e assim como qualquer algoritmo ele funcionará para uma finalidade específica. Por isso, como sempre, conhecer bem o problema, pré-processar os dados corretamente e aplicar técnicas diferentes certamente trarão resultados melhores.