“真金不怕火煉”
(Dito chinês: “O ouro verdadeiro não teme o teste do fogo”)
As opiniões emitidas neste trabalho são de inteira responsabilidade dos autores, não exprimindo, necessariamente, o ponto de vista das instituições às quais estão ou estiveram vinculados.
Motivação
COVID-19 (SARS-CoV-2) é uma pandemia vigente que já infectou mais de 2 milhões de pessoas em todo o mundo e já fez mais de 160 mil vítimas fatais. Diferentemente de todas as outras pandemias já registradas na história, grande volume de dados e notícias sobre o COVID-19 são disponibilizadas com grande velocidade e abrangência, mobilizando estudiosos de variados campos do conhecimento para concentrar seus esforços em analisar esses dados e propor soluções.
Em dados de epidemias, é natural observar um crescimento exponencial do número de infectados, em especial nos estágios iniciais da doença. Conforme abordado em posts como este, medidas de isolamento social buscam “achatar a curva”, reduzindo o pico do número de infectados, mas prolongando a “onda” ao longo do tempo. Analogamente, o número de óbitos também segue uma tendência exponencial.
Analisando os dados dos países afetados pela pandemia, é possível observar padrões que são comuns a todos. Apesar da existência de várias peculiaridades como extensão territorial, densidade populacional, temperatura, estação do ano, grau de subnotificação, disciplina social para acatar medidas de isolamento, etc., as quais diferem significativamente entre os diferentes países, o vírus (ainda) não sofreu mutações radicais desde seu surgimento na China, de modo que os parâmetros gerais de infectividade e letalidade são similares entre os países. No entanto, os dados chineses são uma notória exceção, apresentando um comportamento que difere dos demais – apesar de ser o primeiro país afetado pela doença, o crescimento do número de infectados se manteve próximo de uma tendência linear em estágios iniciais, com poucos momentos que sofrem variação abrupta e prolongados períodos marcados pela ausência de variância, ambas tendências pouco usuais na natureza. Veja a seguir alguns gráficos:
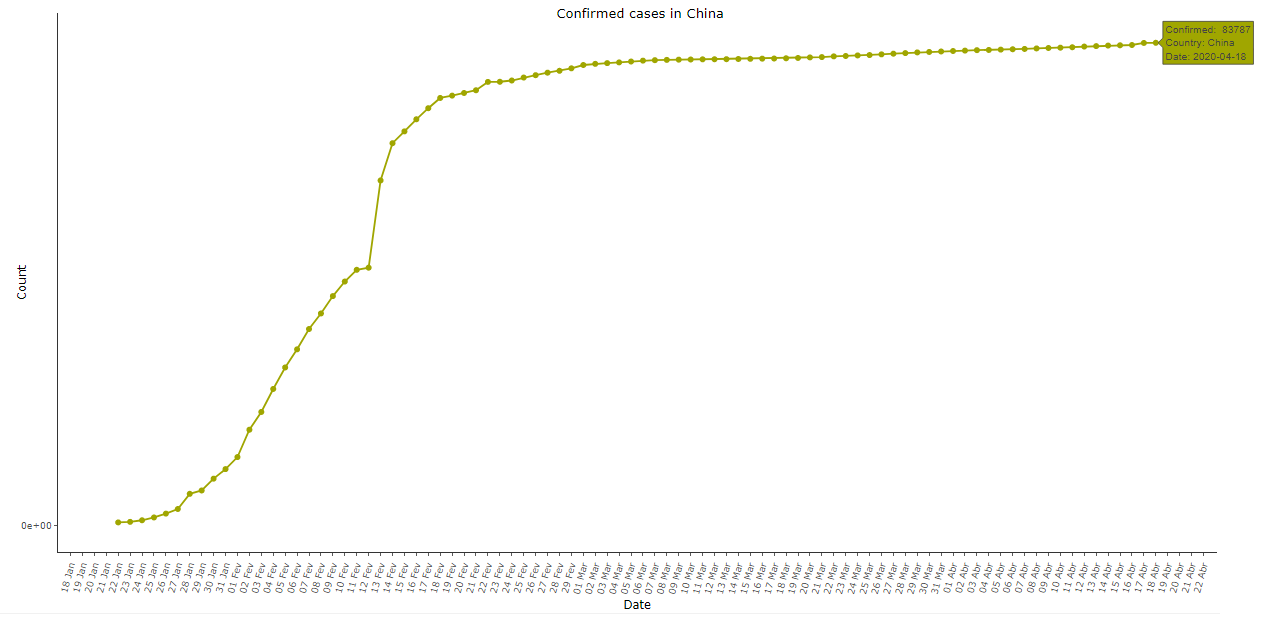Imagem 1: Casos acumulados de COVID-19 na China, dados de 18/04/2020
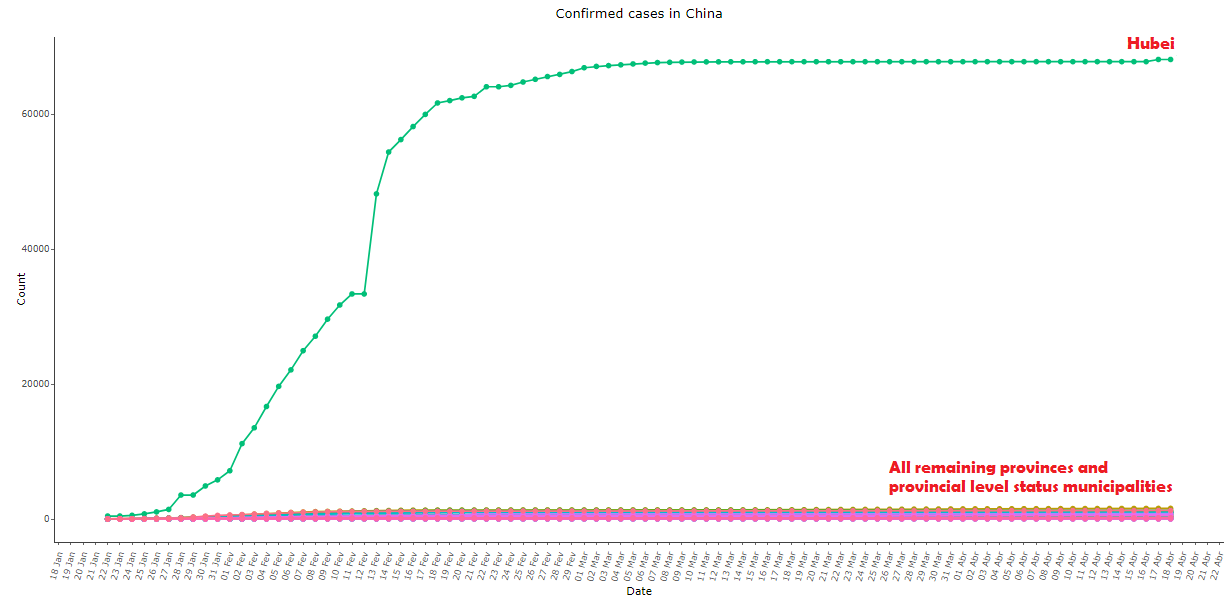Imagem 2: Igual à imagem 1, comparando a província de Hubei com todas as outras províncias
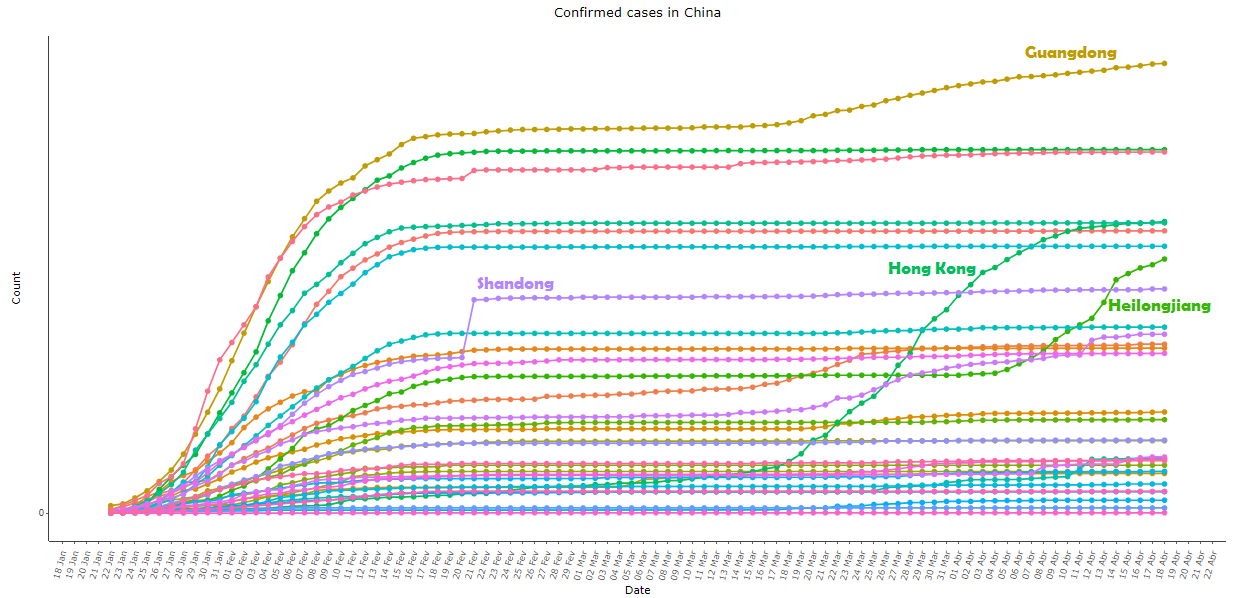Imagem 3: Igual à imagem 2, com todas as províncias exceto Hubei, com escala ajustada para melhor visualização
A imagem 1 acima mostra o número acumulado de casos confirmados de COVID-19 na China (não inclui Taiwan). Note que o padrão exponencial aparece no início mas a concavidade da curva muda rapidamente, ao contrário do esperado e observado em praticamente todos os outros países. O crescimento acontece com “saltos” no início da série, seguido por uma tendência praticamente linear nos primeiros dias de fevereiro, um único dia de grande crescimento, e um longo período com cada vez menos casos novos por dia, até se tornar praticamente uma linha reta a partir do início de março.
Ademais, vendo a decomposição do dado agregado para nível de província na imagem 2, é possível notar que uma única província – Hubei – puxa praticamente toda a série da China, enquanto que todas as outras províncias (as quais também diferem bastante em área, densidade populacional, temperatura, distância com a cidade de origem do vírus, etc.) apresentam praticamente o mesmo padrão, resultando numa curva sigmóide praticamente cirúrgica.
A nível de província, o único local que apresentou algum grau de variância ao longo do tempo foi Hong Kong; em Shandong, observou-se uma grande variação num único dia – 21/02/2020, quando foi notificado um surto do vírus na penitenciária de Rencheng da cidade de Jining: nesse dia 203 pessoas foram adicionadas à estatística de confirmados, um ponto isolado numa curva “bem comportada” em todos os períodos além desse dia. Em Guangdong (no sul da China) e em Heilongjiang (no nordeste da China) a série voltou a apresentar crescimento no fim de março e no início de abril, respectivamente, ambos após um longo período praticamente sem variações. Veja o comportamento das séries dessas províncias na imagem 3.
Para efeito de comparação, veja as séries dos casos de COVID-19 em cada estado dos Estados Unidos:
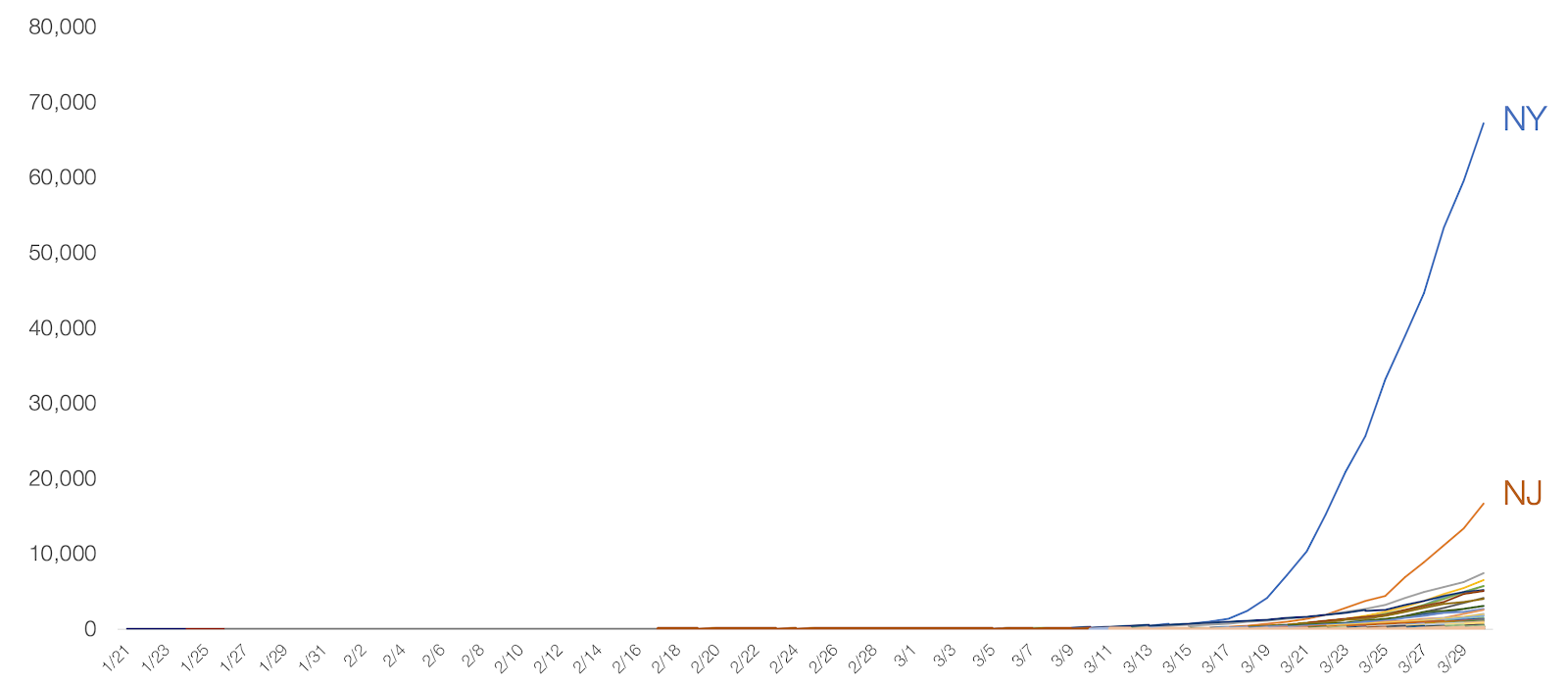Imagem 4: Casos acumulados de COVID-19 por estado dos Estados Unidos, dados de 30/03/2020. Retirado de “Coronavirus: Out of Many, One” por Tomas Pueyo
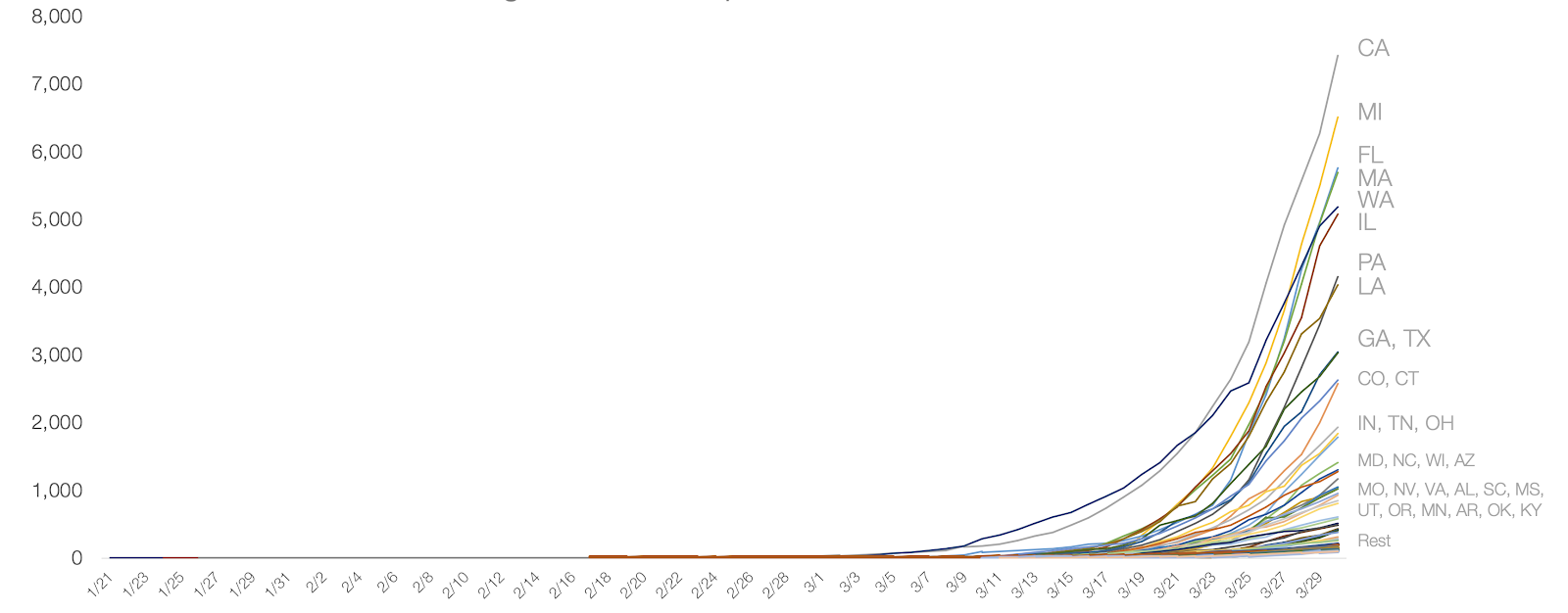Imagem 5: Igual à imagem 4, com todas as províncias exceto New York e New Jersey. Retirado de “Coronavirus: Out of Many, One” por Tomas Pueyo
É bem sabido que a derivada de uma função exponencial também é uma exponencial, então é de se esperar que a variação diária do número de confirmados também siga uma exponencial. Os dados chineses, porém, mostraram algo bem diferente:
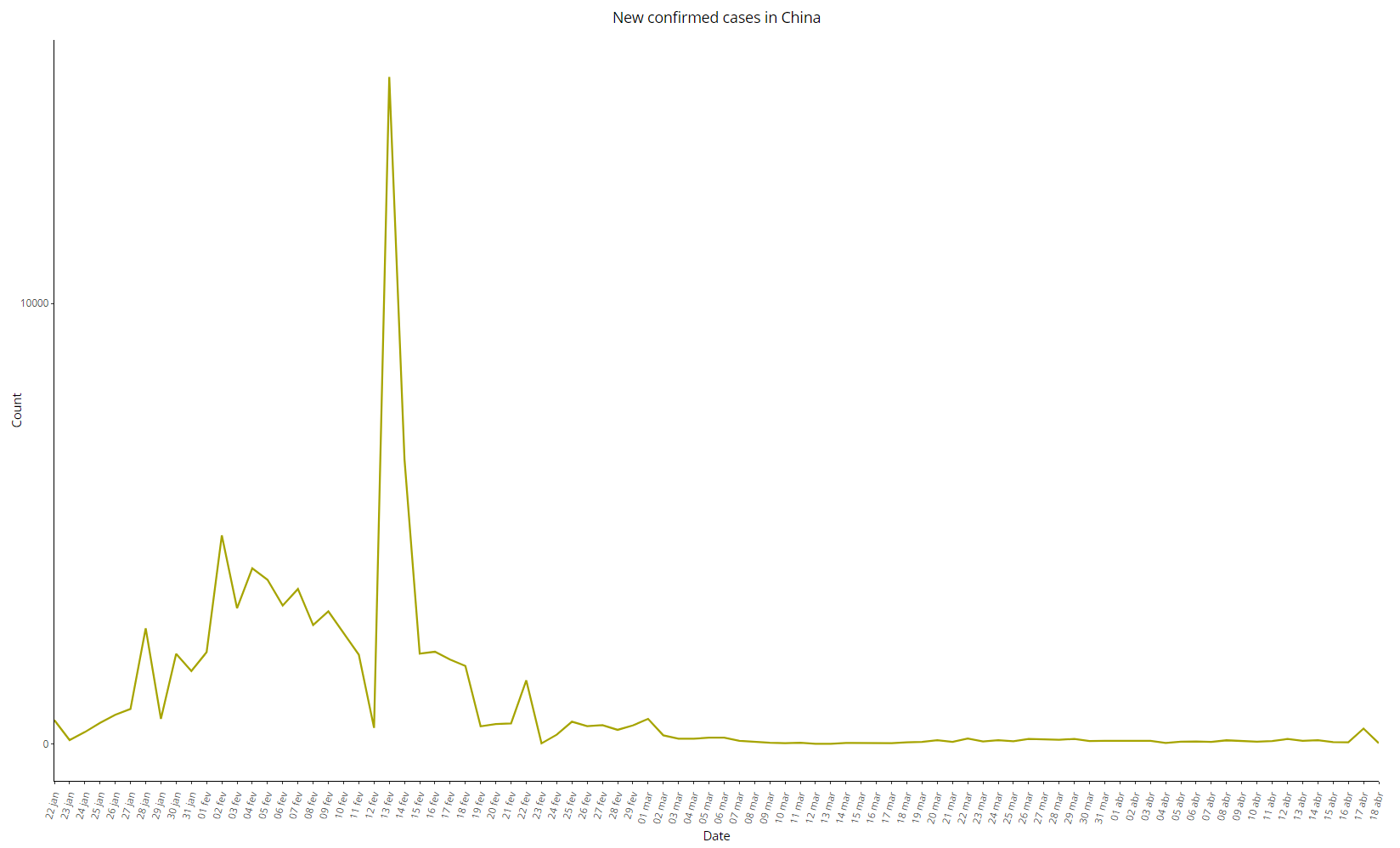Imagem 6: Variação diária de casos de COVID-19 na China, dados de 18/04/2020
O segmento inicial da série mais se assemelha a uma reta do que uma exponencial considerando os dois picos em 28/01 e 02/02, enquanto que o número de novos casos diminuiu rapidamente e sem grandes variações – exceto o pico de 15136 novos casos no dia 13/02/2020, que claramente destoa dos demais períodos. Desconsiderando esse ponto anômalo, é possível enxergar uma tendência praticamente linear entre 02/02 e 23/02, data a partir da qual a série praticamente vira uma linha reta – novamente, um padrão raro em doenças contagiosas.
Veja abaixo o mesmo gráfico comparando a província de Hubei com todas as demais províncias:
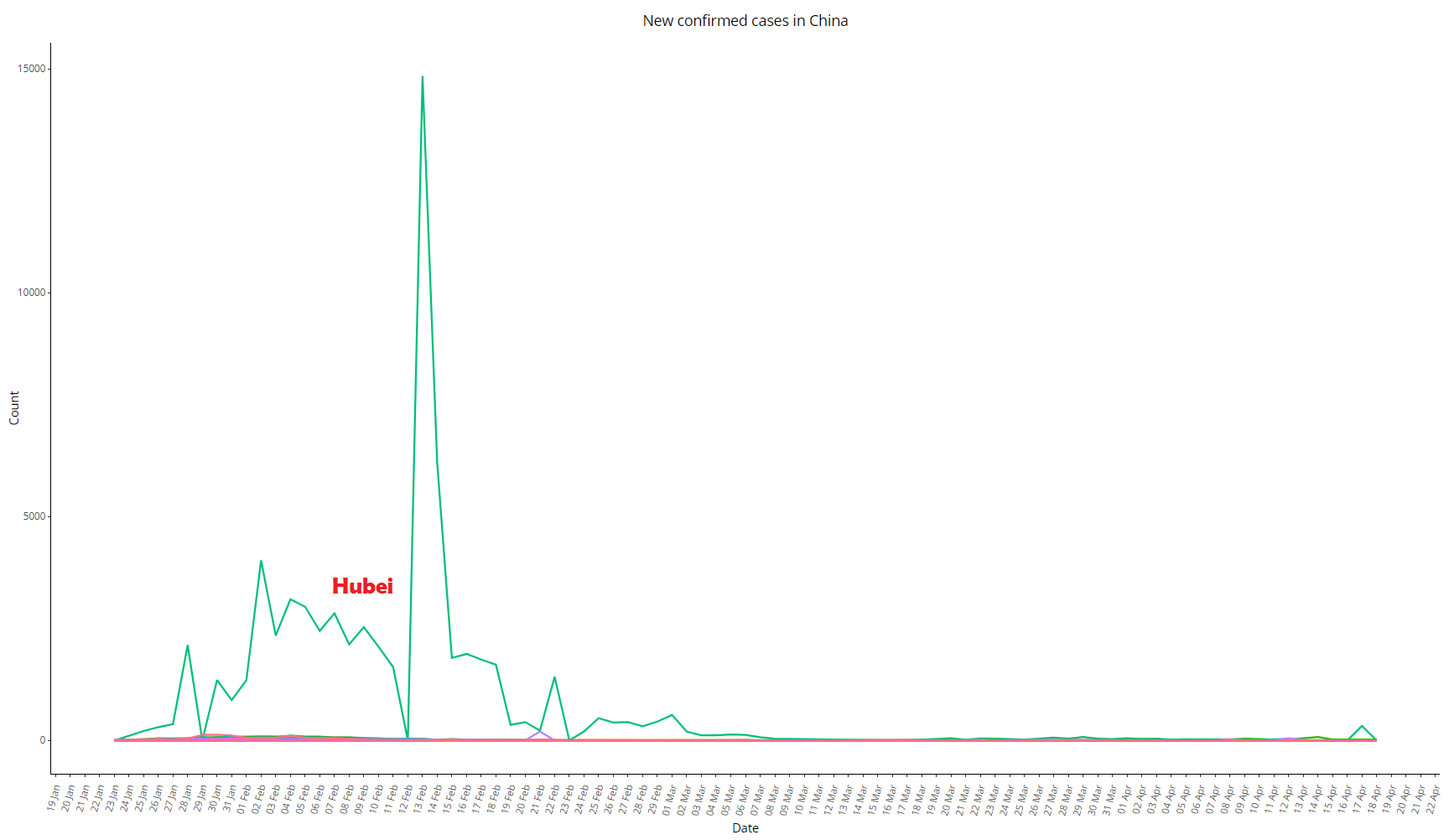Imagem 7: Variação diária de casos de COVID-19 na China, dados de 18/04/2020, comparando Hubei com todas as outras províncias
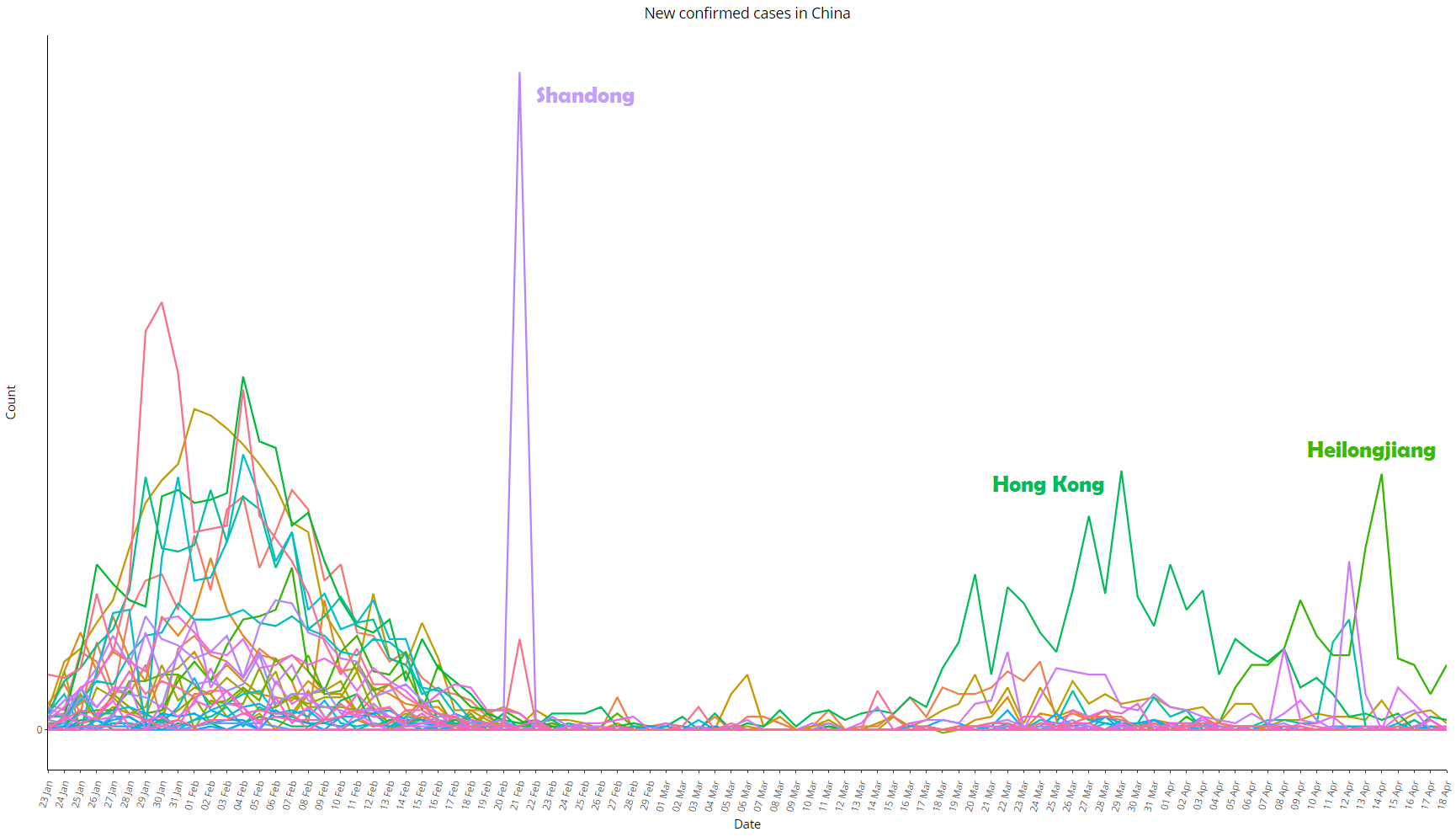Imagem 8: Igual à imagem 7, com todas as províncias exceto Hubei, com escala ajustada para melhor visualização
Vale notar que, no mesmo dia que houve esse pico, Jiang Chaoliang e Ma Guoqiang foram exonerados: eles eram o Nº 1 e o Nº 2 na hierarquia de comando de Hubei (secretário-geral e vice secretário-geral do Partido na província, respectivamente).
Os dados chineses de óbitos por COVID-19 são igualmente anti-intuitivos, veja abaixo nas imagens 9 a 11. Note que a província com mais mortes registradas foi Henan, que é vizinha de Hubei, com apenas 22 óbitos. A variação diária de mortos é uma série praticamente estacionária, temperada com o bizarro “ajuste” de 1290 mortes em 17/04 após mais de um mês quase sem mortes oficiais:
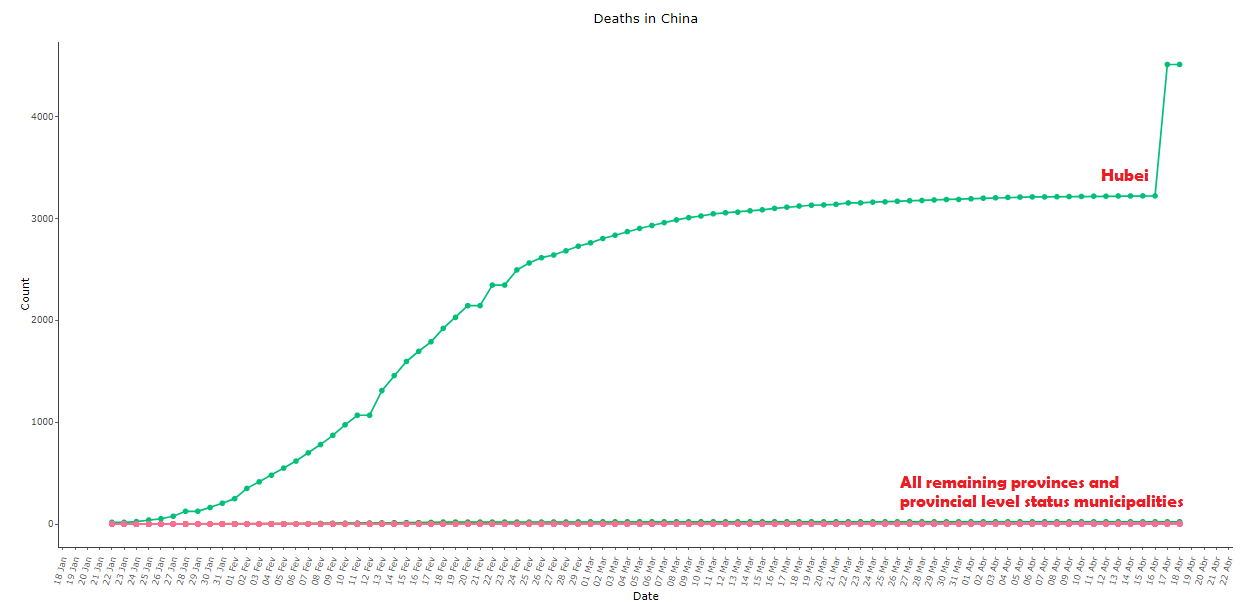Imagem 9: Óbitos totais por COVID-19 na China, dados de 18/04/2020, comparando Hubei com todas as outras províncias
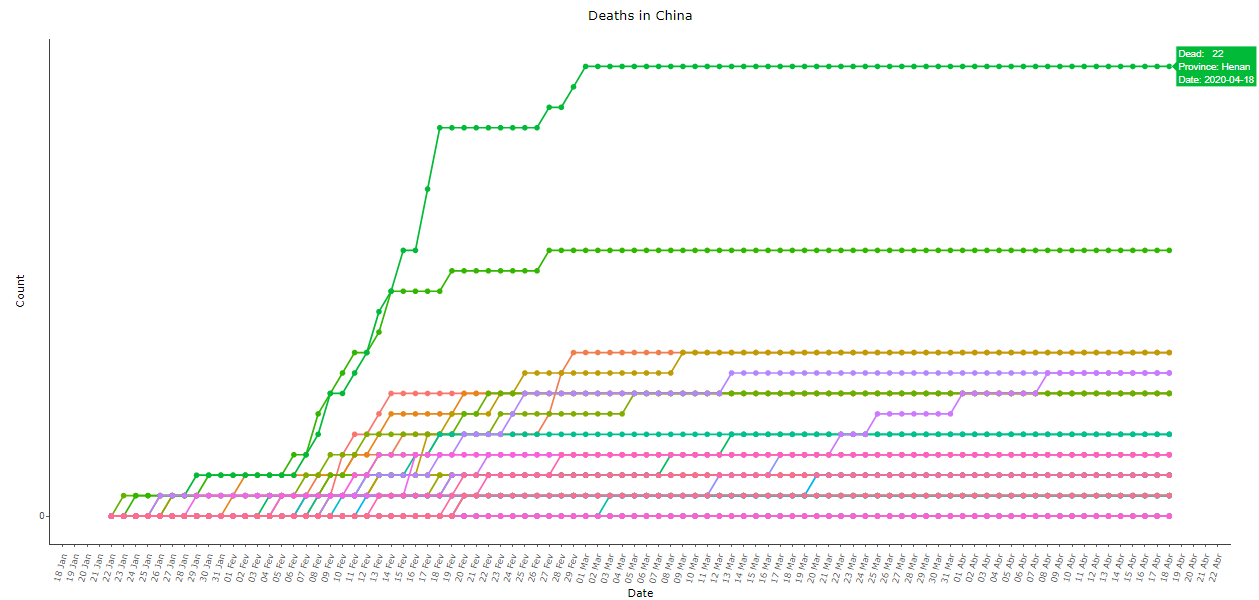Imagem 10: Igual à imagem 9, com todas as províncias exceto Hubei, com escala ajustada para melhor visualização
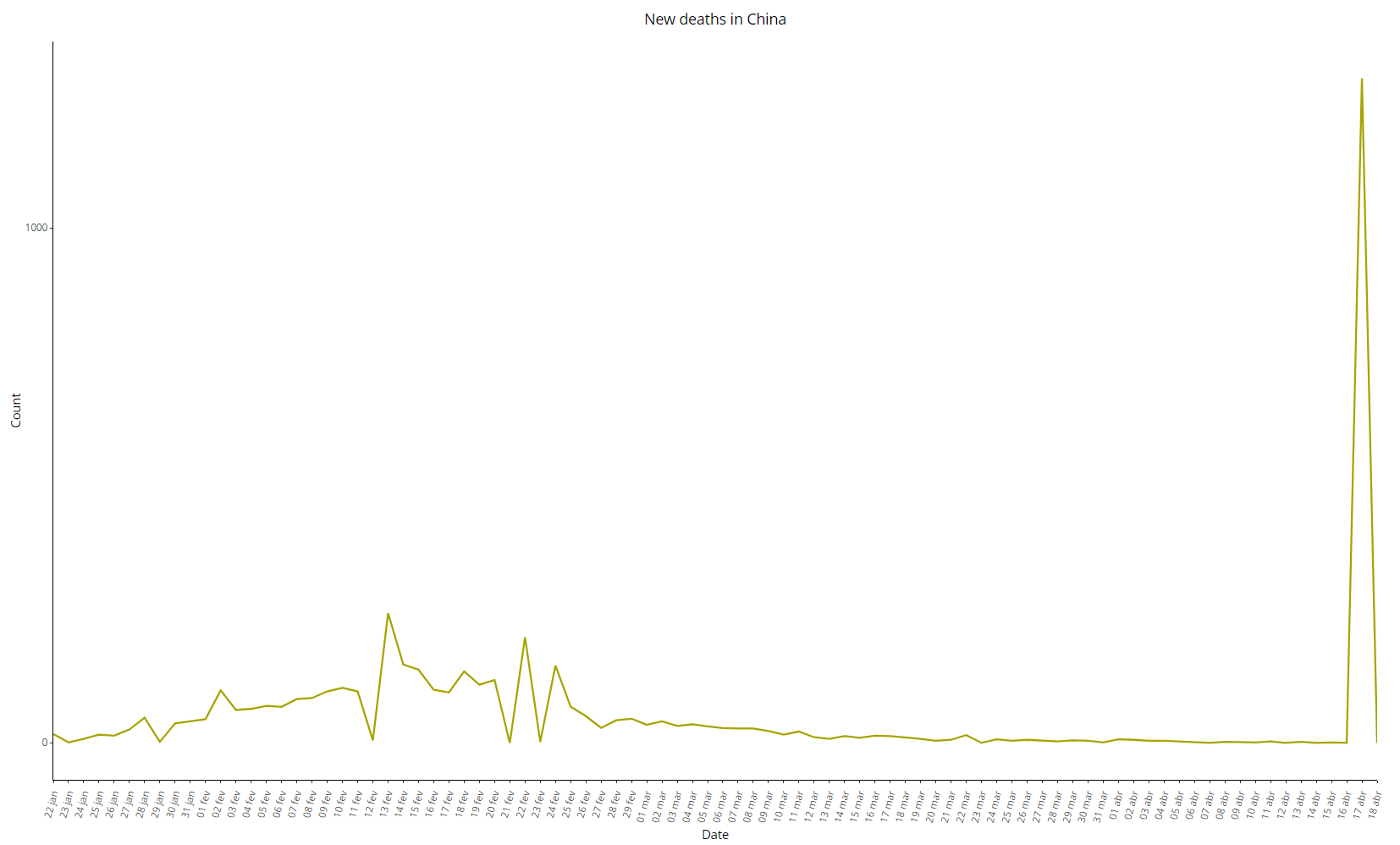Imagem 11: Variação diária de óbitos por COVID-19 na China, dados de 18/04/2020
A adoção de medidas severas de isolamento social influenciam diretamente no formato das curvas, porém o padrão exponencial se mantém pelo menos nos estágios iniciais, e seus efeitos também demoram um certo tempo para se tornarem evidentes. Compare abaixo com dados de Japão, Singapura e Coreia do Sul, que responderam à doença nos estágios iniciais, bem como da Itália, Espanha e Reino Unido, que agiram com maior intensidade apenas em estágios mais avançados:
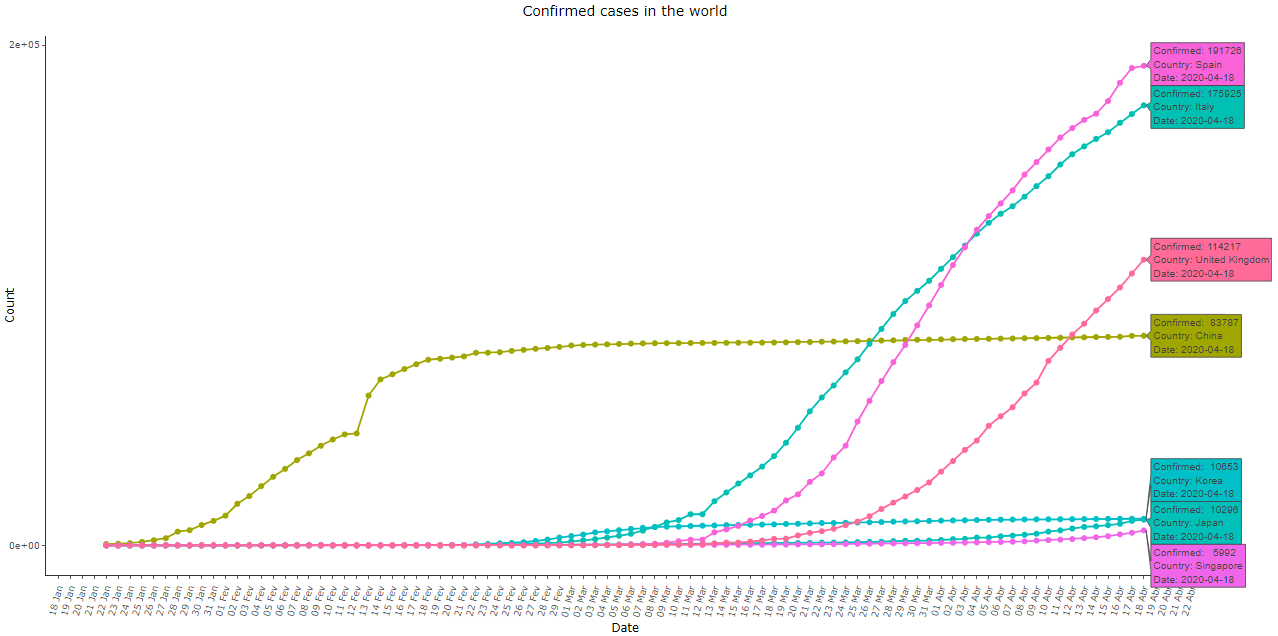Imagem 12: Casos totais de COVID-19 na Espanha, Itália, Reino Unido, China, Coreia do Sul, Japão e Singapura, dados de 18/04/2020
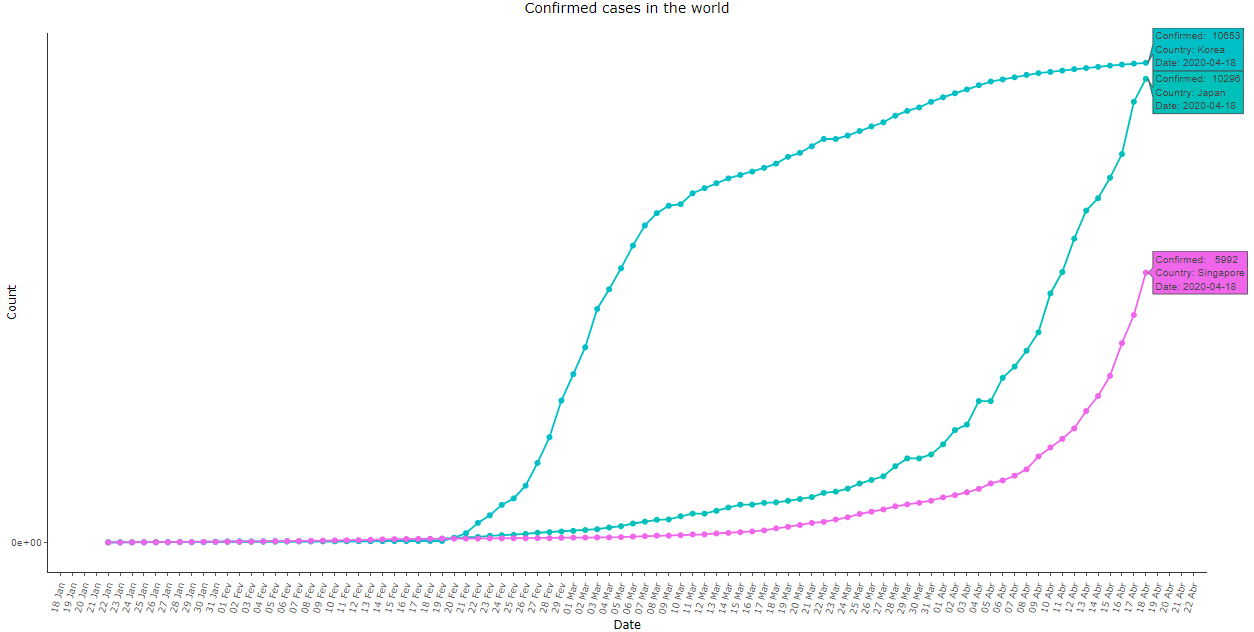Imagem 13: Igual à imagem 12, com os países asiáticos exceto China. Note que Japão e Singapura também apresentaram um crescimento exponencial que começou mais tarde. Apenas a curva da Coreia do Sul apresentou um formato que se assemelha aos dados da China
Com a análise visual acima é possível deduzir que existe algum “padrão” subjacente aos dados do COVID-19, mas que por alguma razão não aparece nos dados da China. Vamos fazer a seguir um exercício de tentar identificar esse padrão usando a Lei de Benford.
Lei de Benford
A vida é misteriosa e padrões inesperados governam o mundo. Como dizem por aí, “a vida imita a arte”. Quando, entretanto, a arte tenta imitar a vida, podemos sentir algo estranho, como se a complexidade da vida não pudesse ser substituída pela ingênua engenhosidade humana.
Um desses padrões que parecem “emergir” na natureza é Lei de Benford, descoberta por Newcomb (1881) e popularizada por Benford (1938), muito usada para verificar fraudes em base de dados.
Benford mostrou que, para mais de 20 variáveis de contextos, tais como tamanhos de rio, população de cidades, constantes da física, taxa de mortalidade, etc., a chance do primeiro dígito de um número ser 1 é a mais alta, chance que vai diminuindo progressivamente com os algarismos subsequentes. Ou seja, é mais provável que o primeiro algarismo do número seja o número 1. Em seguida, o 2, e sucessivamente até o 9.
Okhrimenko e Kopczewski (2019), dois economistas comportamentais, testaram a capacidade das pessoas de criar dados falsos, com o intuito de burlar a base tributária. Os autores encontraram clara evidência de que pelo critério da lei de Benford, o sistema facilmente identificaria os dados falsos. Outras aplicações da Lei de Benford para identificação de dados manipulados e detecção de fraudes incluem Hales et al.(2008), Abrantes-Metz et al. (2012) e Nigrini (2012).
Como explicar intuitivamente essa regularidade aparentemente sem sentido? A resposta está relacionada a dois conceitos conhecidos: a função exponencial e a escala logarítmica. Vamos revisá-las pois elas estão por toda a parte, em especial durante a presente pandemia…
Epidemias como a do Coronavirus, a qual estamos vivendo nesse momento, são clássicos exemplos para explicar a função exponencial. A modelagem acontece da seguinte forma: a quantidade de infectados amanhã \(I_1\) é igual a uma constante \(\alpha\) vezes a quantidade de infectados hoje \(I_0\); ou seja, \(I_1 = \alpha \cdot I_0\).
Supondo que a taxa seja a mesma para amanhã (podemos interpretar como sendo que nenhuma política ou mudança de hábitos da população tenha ocorrido), A quantidade de pessoas infectadas depois de amanhã, \(I_2\), é uma proporção do que é amanhã (\(I_2=\alpha \cdot I_1\)), que por sua vez pode ser substituído por \(I_2=\alpha \cdot I_1 = \alpha \cdot \alpha \cdot I_0\). Com perspicácia, percebemos que podemos generalizar essa fórmula para daqui a \(t\) dias: sendo \(t\) qualquer número inteiro positivo que quisermos, a generalização é \(I_t=\alpha^t \cdot I_0\). O praticamente onipresente regime de juros compostos dos números financeiros também segue essa mesma lógica (\(F = P(1+i)^n\)).
Aqui está o segredo da lei de Benford. Vejamos a simulação de crescimento da epidemia exponencialmente, isso é, cada dia é um múltiplo fixo do dia anterior. Analisemos na escala padrão e na escala logarítmica ao longo do tempo (nesse caso usamos exponenciais de 2, mas poderia ser qualquer número-base). Veja que nos dois casos, cada gradação de azul é a área referente a um dígito. A primeira corresponde entre 10 e 20, a segunda entre 20 e 30, assim sucessivamente até o número 100. Veja que essa distância é diferente na escala padrão e na escala logarítmica.
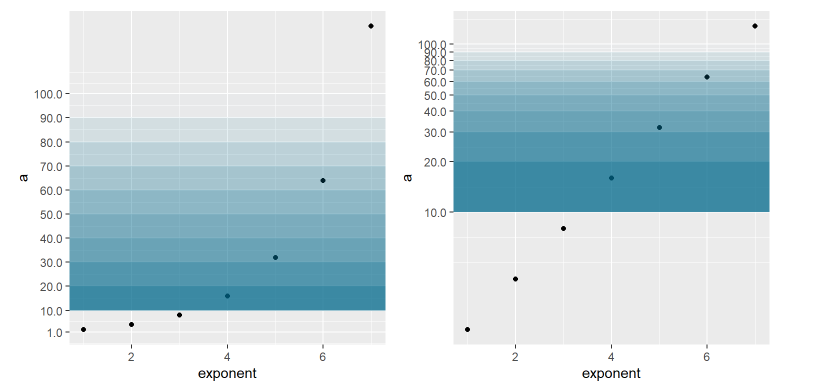Imagem 14: Função exponencial e escala logarítmica
Esse gráfico já nos dá uma pista de porque fenômenos exponenciais podem obedecer a lei de Benford. Quando olhamos pelas lentes logarítmicas, uma função exponencial se parece uma função que cresce linearmente, que cada observação é equidistante das observações antes e depois. Todavia, nessa mesma lente logarítmica, a área que existe entre 10 e 20 é maior a que existe entre 20 e 30, e assim succesivamente. Isso quer dizer que a probabilidade da variável cair nas faixas iniciais é maior que nas faixas seguintes.
Usando um jargão técnico, a mantissa dos logs é uniformemente distribuída. Para o número \(x\) que conseguimos da amostra, vamos aplicar o seu log – por exemplo, apliquemos o log para o número 150: \(log_{10} (150) \approx 2.176\). Podemos decompor o resultado na parte inteira \(m = 2\) e na parte decimal \(d = 0.176\). A parte decimal é a que chamamos de mantissa.
Mantissa e distribuição teórica \(D_T\)
Pelas propriedades do logaritmo, \(log_{10} (150) = log_{10}(100 \cdot 1.5) = log_{10}(100) + log_{10}(1.5) = 2 + 0.176\). Observe que o log na base 10 de qualquer potência inteira de 10 (100, 1000, 10000…) vai resultar em um número inteiro. Nesse sentido, a parte inteira do log na base 10 retorna a quantidade de algarismos que o número original tem (já que o sistema numérico indo-arábico possui 10 algarismos). A mantissa, por outro lado, é o responsável por dizer qual é o primeiro algarismo.
Na casa das centenas, enquanto a mantissa estiver no intervalo \([0, 0.301)\), o número original estará entre \([100, 200)\). Fazendo o mesmo procedimento anterior, quando o número chegar em 200, o seu log resultará em \(log_{10}(200) = log_{10}(100 \cdot 2) = log_{10}(100) + log_{10}(2)\) que resulta em \(2 + 0.301\).
Como vimos que a mantissa é decisiva para saber o primeiro dígito, podemos finalmente entender a lei de Benford. A sua ideia é que a mantissa tem distribuição uniforme para os dígitos de 1 a 9. Assim, é mais fácil occorrer o dígito número 1 por que ele tem o maior intervalo da mantissa \([0, 0.301)\).
Podemos definir, de acordo com a lei de Benford, a probabilidade de um múnero possuir primeiro dígito \(d\), dada por:
\begin{equation} P(d)=\log_{10}\left(1+\frac{1}{d}\right), d = 1,…,9 \end{equation}
Para poupar tempo do leitor, calculamos a distribuição de probabilidade de cada dígito ser o primeiro de acordo com a Lei de Benford (\(D_T\)), bem como os respectivos intervalos na mantissa:
Tabela 1 : Distribuição do primeiro dígito de acordo com a Lei de Benford
Para mais detalhes sobre a lei de Benford e suas aplicações, dê uma olhada nesses links [1; 2; 3]
Distribuições empíricas \(D_E\) dos dados do COVID-19
Para este exercício, escolhemos os países com mais de 10000 casos confirmados de COVID-19 em 18/04/2020, de acordo com os dados disponíveis neste link. Vejamos a seguir como ficou a distribuição do primeiro dígito para as séries temporais de casos e óbitos por COVID-19 dos 24 países selecionados:
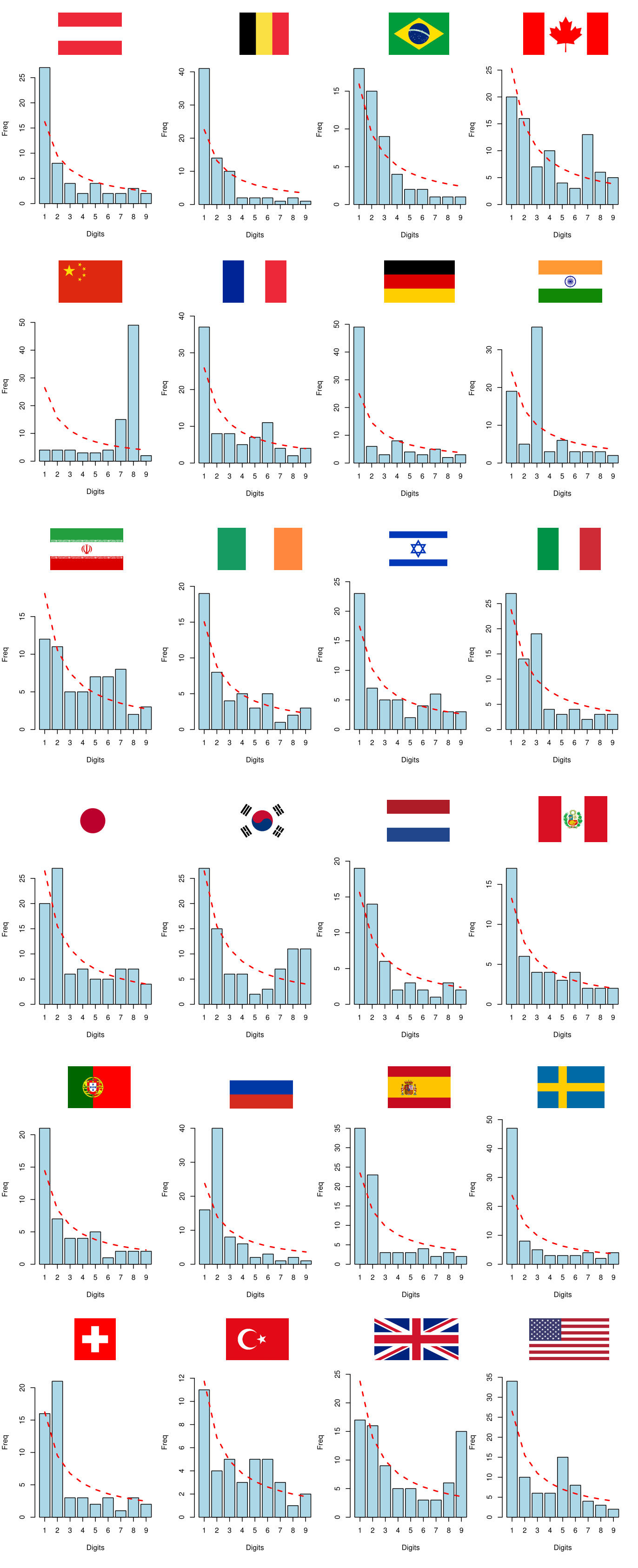Imagem 15: Distribuição do primeiro dígito das séries de casos de COVID-19
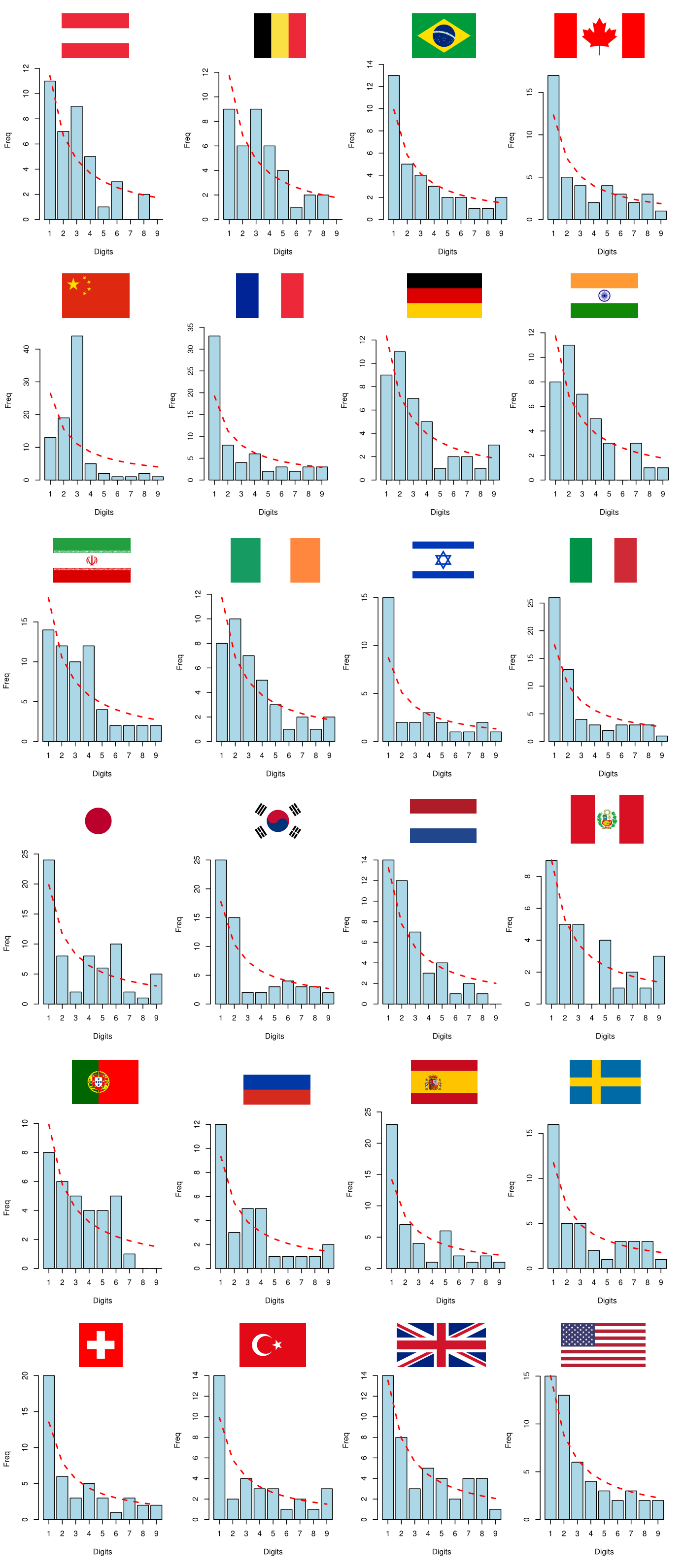Imagem 16: Distribuição do primeiro dígito das séries de óbitos por COVID-19
Nenhuma base de dados segue perfeitamente a Lei de Benford, mas as distribuições empíricas da China parecem ser particularmente diferentes das dos demais países. Pela inspeção visual, os dados da China parecem destoar significativamente da Lei de Benford. Para maior robustez, vamos comparar as distribuições empíricas \(D_E\) com a distribuição teórica \(D_T\) que vem da Lei de Benford realizando alguns testes de hipóteses.
Testes de hipóteses
Para este exercício, vamos realizar três testes de hipóteses:
- Teste qui-quadrado
- Teste Kolmogorov-Smirnov (bicaudal)
- Teste de Kuiper
Os três testes acima são parecidos, todos têm como hipótese nula a igualdade entre as distribuições empírica (\(D_E\)) e teórica (\(D_T\)). O teste qui-quadrado é o mais comumente utilizado, porém tende a rejeitar a hipótese nula mais facilmente, enquanto que o teste KS é menos sensível a diferenças pontuais; o teste de Kuiper funciona da mesma forma que o teste KS, com a diferença que considera separadamente diferenças positivas e negativas entre as distribuições (o caso “\(D_E\) maior que \(D_T\)” é encarado como diferente do caso “\(D_T\) maior que \(D_E\)”). A tabela com os p-valores associados está abaixo:
| País/Teste | Qui-quadrado | Kolmogorov-Smirnov | Kuiper |
|---|---|---|---|
| Áustria | 0.1644 | 0.3364 | 0.7292 |
| Bélgica | 0.0004 | 0.0366 | 0.0521 |
| Brasil | 0.2685 | 0.1243 | 0.4969 |
| Canadá | 0.0117 | 1.0000 | 1.0000 |
| China | 0.0000 | 0.0086 | 0.0521 |
| França | 0.0363 | 0.9794 | 1.0000 |
| Alemanha | 0.0000 | 0.3364 | 0.4969 |
| Índia | 0.0000 | 0.1243 | 0.7292 |
| Irã | 0.1284 | 0.6994 | 0.7292 |
| Irlanda | 0.8036 | 0.9794 | 0.7292 |
| Israel | 0.5245 | 0.9794 | 0.7292 |
| Itália | 0.0705 | 0.1243 | 0.0521 |
| Japão | 0.0509 | 0.9794 | 0.7292 |
| Coreia do Sul | 0.0002 | 0.9794 | 0.7292 |
| Países Baixos | 0.4804 | 0.3364 | 0.7292 |
| Peru | 0.9629 | 0.6994 | 0.7292 |
| Portugal | 0.6247 | 0.3364 | 0.4969 |
| Rússia | 0.0000 | 0.1243 | 0.1797 |
| Espanha | 0.0027 | 0.0366 | 0.1797 |
| Suécia | 0.0000 | 0.1243 | 0.4969 |
| Suíça | 0.0111 | 0.1243 | 0.1797 |
| Turquia | 0.6985 | 0.9794 | 0.7292 |
| Reino Unido | 0.0000 | 0.9794 | 0.9761 |
| Estados Unidos | 0.0156 | 0.6994 | 0.7292 |
Tabela 2 : P-valores para os testes de hipótese para dados de casos de COVID-19, arredondado para quatro casas decimais. Valores significantes ao nível de confiança de 95% estão em negrito
| País/Teste | Qui-quadrado | Kolmogorov-Smirnov | Kuiper |
|---|---|---|---|
| Áustria | 0.2883 | 0.6994 | 0.4969 |
| Bélgica | 0.3746 | 0.9794 | 0.4969 |
| Brasil | 0.9773 | 0.9794 | 0.9761 |
| Canadá | 0.7868 | 0.9794 | 0.7292 |
| China | 0.0000 | 0.1243 | 0.4969 |
| França | 0.0454 | 0.3364 | 0.7292 |
| Alemanha | 0.5473 | 0.6994 | 0.9761 |
| Índia | 0.3685 | 0.6994 | 0.4969 |
| Irã | 0.2098 | 0.3364 | 0.7292 |
| Irlanda | 0.7039 | 0.9794 | 0.9761 |
| Israel | 0.4175 | 0.6994 | 0.4969 |
| Itália | 0.2414 | 0.3364 | 0.7292 |
| Japão | 0.0203 | 0.6994 | 0.7292 |
| Coreia do Sul | 0.1442 | 0.1243 | 0.7292 |
| Países Baixos | 0.4993 | 0.3364 | 0.4969 |
| Peru | 0.5246 | 0.6994 | 0.7292 |
| Portugal | 0.3712 | 0.6994 | 0.1797 |
| Rússia | 0.6750 | 0.3364 | 0.7292 |
| Espanha | 0.1228 | 0.1243 | 0.4969 |
| Suécia | 0.7078 | 0.9794 | 0.7292 |
| Suíça | 0.6034 | 0.6994 | 0.7292 |
| Turquia | 0.5745 | 0.9794 | 0.7292 |
| Reino Unido | 0.8325 | 0.9794 | 0.7292 |
| Estados Unidos | 0.9284 | 0.6994 | 0.9761 |
Tabela 3 : P-valores para os testes de hipótese para dados de óbitos por COVID-19, arredondado para quatro casas decimais. Valores significantes ao nível de confiança de 95% estão em negrito
Basicamente, quanto menor o p-valor, menos os dados do respectivo país parecem “obedecer” à Lei de Benford. Usando essa métrica de avaliação, os dados chineses claramente são anômalos em relação à Lei de Benford, ao passo que a grande maioria dos outros países parecem segui-la razoavelmente bem.
Distância KL e clusterização por DBSCAN
Vamos ver agora o quão “parecidos” são os dados dos países entre si, utilizando uma métrica chamada Distância de Kullback-Leibler (doravante “distância KL”), a qual é uma medida de entropia relativa entre duas distribuições de probabilidade. Seu cálculo para distribuições discretas se dá mediante a seguinte expressão:
\begin{equation} KL(D_1||D_2) = \sum\limits_{x \in \mathcal{P}}{D_1(x)\cdot log\left(\frac{D_1(x)}{D_2(x)}\right)} \end{equation}
A distância KL fornece o valor esperado da diferença logarítmica entre duas distribuições \(D_1\) e \(D_2\) definidas no mesmo espaço de probabilidade \(\mathcal{P}\); a discussão teórica da esse conceito está além dos escopos deste post, pois envolve conhecimentos de teoria da informação e teoria da medida. Em termos simplificados, a distância KL mede o quão diferentes são duas distribuições de probabilidade – quanto mais próximo de zero, mais “parecidas” elas são. Como são 24 países, ao compararmos todas as distribuições empíricas \(D_E\) obtemos como resultado matrizes 24x24 que medem a “diferença” entre os dados dos países considerados (uma para dados de casos e outra para dados de óbitos), matrizes cujas diagonais principais são toda zero (a “diferença” de algo com ela mesma é igual a zero!).
Apresentamos na tabela 4 abaixo a matriz de distâncias KL entre as distribuições empíricas dos dados de casos confirmados dos 24 países selecionados. Para economizar espaço, omitimos a matriz calculada a partir dos dados de óbitos.
| Áustria | Bélgica | Brasil | Canadá | China | França | Alemanha | Índia | Irã | Irlanda | Israel | Itália | Japão | Coreia do Sul | Países Baixos | Peru | Portugal | Rússia | Espanha | Suécia | Suíça | Turquia | Reino Unido | Estados Unidos | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Áustria | 0.0000 | 0.0409 | 0.0734 | 0.1005 | 0.5631 | 0.0387 | 0.0447 | 0.1739 | 0.1223 | 0.0371 | 0.0395 | 0.0595 | 0.0921 | 0.0778 | 0.0313 | 0.0268 | 0.0146 | 0.1832 | 0.0362 | 0.0214 | 0.0812 | 0.0826 | 0.1109 | 0.0410 |
| Bélgica | 0.0409 | 0.0000 | 0.0452 | 0.1612 | 0.7024 | 0.0812 | 0.0956 | 0.1827 | 0.1964 | 0.0727 | 0.0819 | 0.0488 | 0.1466 | 0.1303 | 0.0397 | 0.0704 | 0.0556 | 0.1564 | 0.0539 | 0.0455 | 0.0995 | 0.1418 | 0.1662 | 0.1019 |
| Brasil | 0.0734 | 0.0452 | 0.0000 | 0.0981 | 0.5960 | 0.1057 | 0.1721 | 0.1647 | 0.1151 | 0.0601 | 0.0887 | 0.0252 | 0.0707 | 0.1151 | 0.0235 | 0.0650 | 0.0670 | 0.0532 | 0.0693 | 0.1201 | 0.0533 | 0.1100 | 0.0990 | 0.1111 |
| Canadá | 0.1005 | 0.1612 | 0.0981 | 0.0000 | 0.3342 | 0.1223 | 0.1370 | 0.2187 | 0.0409 | 0.1111 | 0.0376 | 0.1266 | 0.0310 | 0.0433 | 0.1267 | 0.0698 | 0.0839 | 0.2046 | 0.1453 | 0.1418 | 0.1335 | 0.0830 | 0.0824 | 0.1181 |
| China | 0.5631 | 0.7024 | 0.5960 | 0.3342 | 0.0000 | 0.7432 | 0.7605 | 0.6701 | 0.5725 | 0.6681 | 0.5067 | 0.6763 | 0.4182 | 0.3305 | 0.6036 | 0.5808 | 0.6312 | 0.8489 | 0.7006 | 0.7566 | 0.6211 | 0.6705 | 0.4789 | 0.6572 |
| França | 0.0387 | 0.0812 | 0.1057 | 0.1223 | 0.7432 | 0.0000 | 0.0647 | 0.1576 | 0.0771 | 0.0246 | 0.0361 | 0.0719 | 0.1107 | 0.1180 | 0.0807 | 0.0137 | 0.0647 | 0.2226 | 0.0879 | 0.0524 | 0.1224 | 0.0256 | 0.1278 | 0.0244 |
| Alemanha | 0.0447 | 0.0956 | 0.1721 | 0.1370 | 0.7605 | 0.0647 | 0.0000 | 0.2417 | 0.1751 | 0.0690 | 0.0461 | 0.1260 | 0.1635 | 0.1181 | 0.1170 | 0.0521 | 0.0420 | 0.2765 | 0.0858 | 0.0206 | 0.1607 | 0.1151 | 0.1935 | 0.0691 |
| Índia | 0.1739 | 0.1827 | 0.1647 | 0.2187 | 0.6701 | 0.1576 | 0.2417 | 0.0000 | 0.2459 | 0.2386 | 0.2244 | 0.0706 | 0.2892 | 0.2965 | 0.1888 | 0.2027 | 0.2205 | 0.3063 | 0.3947 | 0.2911 | 0.3474 | 0.1517 | 0.2098 | 0.2509 |
| Irã | 0.1223 | 0.1964 | 0.1151 | 0.0409 | 0.5725 | 0.0771 | 0.1751 | 0.2459 | 0.0000 | 0.0947 | 0.0674 | 0.1353 | 0.0491 | 0.1192 | 0.1351 | 0.0598 | 0.1113 | 0.2188 | 0.1537 | 0.1645 | 0.1445 | 0.0292 | 0.1040 | 0.0680 |
| Irlanda | 0.0371 | 0.0727 | 0.0601 | 0.1111 | 0.6681 | 0.0246 | 0.0690 | 0.2386 | 0.0947 | 0.0000 | 0.0321 | 0.0540 | 0.0644 | 0.0742 | 0.0472 | 0.0068 | 0.0459 | 0.1446 | 0.0583 | 0.0663 | 0.0632 | 0.0446 | 0.0790 | 0.0411 |
| Israel | 0.0395 | 0.0819 | 0.0887 | 0.0376 | 0.5067 | 0.0361 | 0.0461 | 0.2244 | 0.0674 | 0.0321 | 0.0000 | 0.0719 | 0.0621 | 0.0432 | 0.0809 | 0.0184 | 0.0456 | 0.2038 | 0.0847 | 0.0467 | 0.1104 | 0.0476 | 0.0952 | 0.0578 |
| Itália | 0.0595 | 0.0488 | 0.0252 | 0.1266 | 0.6763 | 0.0719 | 0.1260 | 0.0706 | 0.1353 | 0.0540 | 0.0719 | 0.0000 | 0.1031 | 0.1094 | 0.0357 | 0.0558 | 0.0724 | 0.1237 | 0.1236 | 0.1072 | 0.1077 | 0.0759 | 0.0870 | 0.1073 |
| Japão | 0.0921 | 0.1466 | 0.0707 | 0.0310 | 0.4182 | 0.1107 | 0.1635 | 0.2892 | 0.0491 | 0.0644 | 0.0621 | 0.1031 | 0.0000 | 0.0537 | 0.0528 | 0.0651 | 0.0831 | 0.0927 | 0.0679 | 0.1534 | 0.0386 | 0.1049 | 0.0596 | 0.1089 |
| Coreia do Sul | 0.0778 | 0.1303 | 0.1151 | 0.0433 | 0.3305 | 0.1180 | 0.1181 | 0.2965 | 0.1192 | 0.0742 | 0.0432 | 0.1094 | 0.0537 | 0.0000 | 0.0883 | 0.0726 | 0.0863 | 0.2317 | 0.1205 | 0.1145 | 0.1041 | 0.1254 | 0.0397 | 0.1473 |
| Países Baixos | 0.0313 | 0.0397 | 0.0235 | 0.1267 | 0.6036 | 0.0807 | 0.1170 | 0.1888 | 0.1351 | 0.0472 | 0.0809 | 0.0357 | 0.0528 | 0.0883 | 0.0000 | 0.0457 | 0.0423 | 0.0785 | 0.0317 | 0.0859 | 0.0276 | 0.1009 | 0.0683 | 0.0821 |
| Peru | 0.0268 | 0.0704 | 0.0650 | 0.0698 | 0.5808 | 0.0137 | 0.0521 | 0.2027 | 0.0598 | 0.0068 | 0.0184 | 0.0558 | 0.0651 | 0.0726 | 0.0457 | 0.0000 | 0.0328 | 0.1594 | 0.0626 | 0.0530 | 0.0767 | 0.0290 | 0.0820 | 0.0257 |
| Portugal | 0.0146 | 0.0556 | 0.0670 | 0.0839 | 0.6312 | 0.0647 | 0.0420 | 0.2205 | 0.1113 | 0.0459 | 0.0456 | 0.0724 | 0.0831 | 0.0863 | 0.0423 | 0.0328 | 0.0000 | 0.1745 | 0.0625 | 0.0453 | 0.0908 | 0.0611 | 0.0931 | 0.0314 |
| Rússia | 0.1832 | 0.1564 | 0.0532 | 0.2046 | 0.8489 | 0.2226 | 0.2765 | 0.3063 | 0.2188 | 0.1446 | 0.2038 | 0.1237 | 0.0927 | 0.2317 | 0.0785 | 0.1594 | 0.1745 | 0.0000 | 0.0920 | 0.2830 | 0.0342 | 0.2555 | 0.1539 | 0.2438 |
| Espanha | 0.0362 | 0.0539 | 0.0693 | 0.1453 | 0.7006 | 0.0879 | 0.0858 | 0.3947 | 0.1537 | 0.0583 | 0.0847 | 0.1236 | 0.0679 | 0.1205 | 0.0317 | 0.0626 | 0.0625 | 0.0920 | 0.0000 | 0.0725 | 0.0254 | 0.1403 | 0.1252 | 0.0915 |
| Suécia | 0.0214 | 0.0455 | 0.1201 | 0.1418 | 0.7566 | 0.0524 | 0.0206 | 0.2911 | 0.1645 | 0.0663 | 0.0467 | 0.1072 | 0.1534 | 0.1145 | 0.0859 | 0.0530 | 0.0453 | 0.2830 | 0.0725 | 0.0000 | 0.1327 | 0.1115 | 0.1644 | 0.0723 |
| Suíça | 0.0812 | 0.0995 | 0.0533 | 0.1335 | 0.6211 | 0.1224 | 0.1607 | 0.3474 | 0.1445 | 0.0632 | 0.1104 | 0.1077 | 0.0386 | 0.1041 | 0.0276 | 0.0767 | 0.0908 | 0.0342 | 0.0254 | 0.1327 | 0.0000 | 0.1652 | 0.0918 | 0.1397 |
| Turquia | 0.0826 | 0.1418 | 0.1100 | 0.0830 | 0.6705 | 0.0256 | 0.1151 | 0.1517 | 0.0292 | 0.0446 | 0.0476 | 0.0759 | 0.1049 | 0.1254 | 0.1009 | 0.0290 | 0.0611 | 0.2555 | 0.1403 | 0.1115 | 0.1652 | 0.0000 | 0.1053 | 0.0319 |
| Reino Unido | 0.1109 | 0.1662 | 0.0990 | 0.0824 | 0.4789 | 0.1278 | 0.1935 | 0.2098 | 0.1040 | 0.0790 | 0.0952 | 0.0870 | 0.0596 | 0.0397 | 0.0683 | 0.0820 | 0.0931 | 0.1539 | 0.1252 | 0.1644 | 0.0918 | 0.1053 | 0.0000 | 0.1764 |
| Estados Unidos | 0.0410 | 0.1019 | 0.1111 | 0.1181 | 0.6572 | 0.0244 | 0.0691 | 0.2509 | 0.0680 | 0.0411 | 0.0578 | 0.1073 | 0.1089 | 0.1473 | 0.0821 | 0.0257 | 0.0314 | 0.2438 | 0.0915 | 0.0723 | 0.1397 | 0.0319 | 0.1764 | 0.0000 |
Tabela 4: Matriz de distâncias KL entre as distribuições do primeiro dígito do número de casos de COVID-19 dos países analisados, arredondado para quatro casas decimais
A matriz acima não tem uma interpretação prática muito imediata, então aplicamos um algoritmo de clusterização para definir quais são os países que se parecem mais entre si – pares de países com grande distância KL são menos parecidos entre si que pares de países com baixa distância KL. O algoritmo escolhido foi o DBSCAN, que cria clusters para cada ponto da amostra com base no número mínimo de pontos em cada cluster (\(mp\)) e na distância máxima que um ponto pode estar em relação a outro ponto do mesmo cluster (\(\varepsilon\)). Pontos que não possui pelo menos \(mp\) pontos dentro do raio de \(\varepsilon\) são classificados como outliers sem cluster. Um bom material introdutório sobre o DBSCAN pode ser encontrado em aqui.
Uma das vantagens do DBSCAN é o fato de o número de cluster ser definido automaticamente em vez de escolhido pelo usuário, tornando-o um bom instrumento para a detecção de anomalias. Para este exercício, utilizamos \(mp=3\) e \(\varepsilon\) como sendo a média das distâncias KL entre os países acrescida de três desvios-padrão amostrais. O resultado dessa clusterização é mais fácil de ser interpretada:
| País | Cluster |
|---|---|
| Áustria | 1 |
| Bélgica | 1 |
| Brasil | 1 |
| Canadá | 1 |
| China | Outlier |
| França | 1 |
| Alemanha | 1 |
| Índia | Outlier |
| Irã | 1 |
| Irlanda | 1 |
| Israel | 1 |
| Itália | 1 |
| Japão | 1 |
| Coreia do Sul | 1 |
| Países Baixos | 1 |
| Peru | 1 |
| Portugal | 1 |
| Rússia | 1 |
| Espanha | 1 |
| Suécia | 1 |
| Suíça | 1 |
| Turquia | 1 |
| Reino Unido | 1 |
| Estados Unidos | 1 |
Tabela 5: Clusterização por DBSCAN das distâncias KL entre as distribuições do primeiro dígito do número de casos de COVID-19 dos países analisados
| País | Cluster |
|---|---|
| Áustria | 1 |
| Bélgica | 1 |
| Brasil | 1 |
| Canadá | 1 |
| China | Outlier |
| França | 1 |
| Alemanha | 1 |
| Índia | 1 |
| Irã | 1 |
| Irlanda | 1 |
| Israel | 1 |
| Itália | 1 |
| Japão | 1 |
| Coreia do Sul | 1 |
| Países Baixos | Outlier |
| Peru | Outlier |
| Portugal | Outlier |
| Rússia | 1 |
| Espanha | 1 |
| Suécia | 1 |
| Suíça | 1 |
| Turquia | 1 |
| Reino Unido | 1 |
| Estados Unidos | 1 |
Tabela 6: Clusterização por DBSCAN das distâncias KL entre as distribuições do primeiro dígito do número de óbitos por COVID-19 dos países analisados
Novamente, assim como sugerido pela inspeção visual e pelos testes de hipóteses supramencionados, os resultados indicam que os dados da China apresentam padrões distintos da grande parte dos outros países mais afetados pela pandemia, os quais mostraram padrões similares de infectividade e letalidade: o algoritmo retornou apenas um cluster, classificando China como “outlier” tanto para os dados de casos quanto para os dados de óbitos. De fato, os países categorizados como “cluster 1” parecem seguir melhor a distribuição da Lei de Benford.
Apesar de a China ser o local de origem da doença, dada a grande divergência entre seus dados e os dos demais locais, os dados chineses devem ser utilizados com especial cautela para análises como a estimação dos parâmetros médicos (basic reproducing number, serial interval e case-fatality ratio, por exemplo), a modelagem da dispersão geográfica do patógeno, diagnósticos da eficácia de cenários de intervenção, etc.
Considerações finais
A medida que à pandemia atinge mais e mais pessoas e traz impactos cada vez mais profundos nas atividades econômicas e na vida social a nível global, discutir a subnotificação dos dados do COVID-19 se torna especialmente relevante, tanto para a avaliação da severidade do cenário quanto para a proposição de soluções e meios de enfrentamento da crise. Dado que acadêmicos, pesquisadores e formuladores de políticas públicas do mundo todo estão se dedicando a essa causa, ter em mãos dados precisos e confiáveis é de fundamental importância, pois a qualidade dos dados condiciona diretamente na qualidade de todas as análises que deles derivam. Como diz o ditado: “Garbage in, garbage out!“
Às vezes, “coincidência” é apenas um jeito conveniente de alguém se esquivar dos fatos que ele não conseguiu explicar.
